Charges Q1andQ2 lie inside and outside, respectively, of a closed surface S. Let E be the field at any point on S and ϕ be the flux of E over S.
If Q1 changes both E and ϕ will change
If Q2 changes, will changes but ϕ will not change
If Q1=0 and Q2≠0, then E≠0 but ϕ=0
If Q1≠0 and Q2=0, the E=0 but ϕ≠0
The correct Answer is:A, B, C
To solve the problem, we need to analyze the relationship between the electric field E and the electric flux Φ through a closed surface S when charges Q1 and Q2 are present inside and outside the surface, respectively.
1. Understanding Electric Flux:
The electric flux Φ through a closed surface is given by Gauss's law:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface S and ϵ0 is the permittivity of free space.
2. Identifying Charges:
In this scenario, Q1 is located inside the closed surface S and Q2 is located outside the surface.
3. Calculating Flux:
Since Q2 is outside the surface, it does not contribute to the electric flux through surface S. Therefore, the flux Φ through surface S depends only on Q1:
Φ=Q1ϵ0
4. Effect of Changing Q1:
If Q1 changes, the enclosed charge changes, which directly affects the electric flux Φ. Thus, both the electric field E at any point on the surface and the flux Φ will change when Q1 changes.
5. Effect of Changing Q2:
If Q2 changes, since it is outside the closed surface, it does not affect the enclosed charge Qenc. Therefore, the electric flux Φ remains unchanged. However, the electric field E at the surface may change due to the influence of Q2.
6. Special Cases:
- If Q1=0 (no charge inside), then Φ=0 regardless of Q2.
- If Q2=0 (no charge outside), the electric field E at the surface will still be due to Q1 and will not be zero.
Conclusion:
- The electric flux Φ through the surface S depends only on Q1.
- The electric field E at the surface depends on both Q1 and Q2.
The electric flux Φ through a closed surface is given by Gauss's law:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface S and ϵ0 is the permittivity of free space.
In this scenario, Q1 is located inside the closed surface S and Q2 is located outside the surface.
Since Q2 is outside the surface, it does not contribute to the electric flux through surface S. Therefore, the flux Φ through surface S depends only on Q1:
Φ=Q1ϵ0
If Q1 changes, the enclosed charge changes, which directly affects the electric flux Φ. Thus, both the electric field E at any point on the surface and the flux Φ will change when Q1 changes.
If Q2 changes, since it is outside the closed surface, it does not affect the enclosed charge Qenc. Therefore, the electric flux Φ remains unchanged. However, the electric field E at the surface may change due to the influence of Q2.
- If Q1=0 (no charge inside), then Φ=0 regardless of Q2.
- If Q2=0 (no charge outside), the electric field E at the surface will still be due to Q1 and will not be zero.
- The electric flux Φ through the surface S depends only on Q1.
- The electric field E at the surface depends on both Q1 and Q2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
If charge q1 and q2 lies inside and outside respectively of a closed surface S. Let E be the electric field at any point on S and ϕ be the electric flux over S. Select the incorrect option.
View SolutionIf an isolated infinite plate contains a charge Q1 on one of its surfaces and a charge Q2 on its other surface, then prove that electric field intensity at a point in front of the plate will be Q/2Aε0, where Q=Q1+Q2
View SolutionLet C1 and C2 be respectively, the parabolas x2=y−1 and y2=x−1 Let P be any point on C1 and Q be any point on C2 . Let P1 and Q1 be the refelections of P and Q, respectively with respect to the line y=x.
If the point p(π,π2+1) and Q(μ2+1,μ) then P1 and Q1 areView SolutionLet E1 and E2, be two ellipses whose centers are at the origin.The major axes of E1 and E2, lie along the x-axis and the y-axis, respectively. Let S be the circle x2+(y−1)2=2. The straight line x+ y =3 touches the curves S, E1 and E2 at P,Q and R, respectively. Suppose that PQ=PR=2√23.If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is(are):
View SolutionS1 and S2 are two hollow concentric spheres enclosing charges Q and 2Q, respectively, as shown in figure.
i. What is the ratio of the electric flux through S1 and S2?
ii. How will the electric flux through sphere S1 change if a medium of dielectric constant 5 is introduced in the space inside S1 in place of air.
 .View Solution
.View SolutionShow in the figure are two point charge + Q and - Q inside the cavity of the Spherical .shell the changes are kept near the surface of the cavity on opposite sides of the centre of the shell if σ1 is the surface charge on the inner surface and Q1 net charge on it and σ2 the surface charge on the outer surface and Q2 net charge on it then :
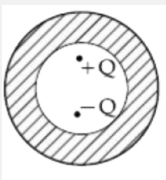 View Solution
View SolutionConsider two charged metallic spheres S1 and S2 of radii R and 4R, respectively. The electric fields E1 (on S1 ) and E2 (on S2) on their surfaces are such that E1E2=51 . Then the ratio V1 (on S1 ) / V1 (on S2 ) of the electrostatic potentials on each sphere is :
View SolutionTwo conducting closed surfaced shells are shown in figure. They are connected by wire through switch S. If q1 and q2 charges are given to inner and outer shells respectively . The switch is closed find the ratio of final charge to initial charge for each shell.
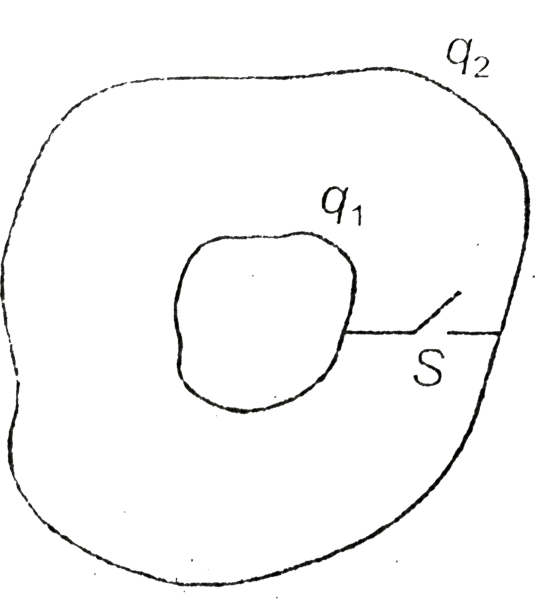 View Solution
View SolutionA charge Q is placed at a distance a2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
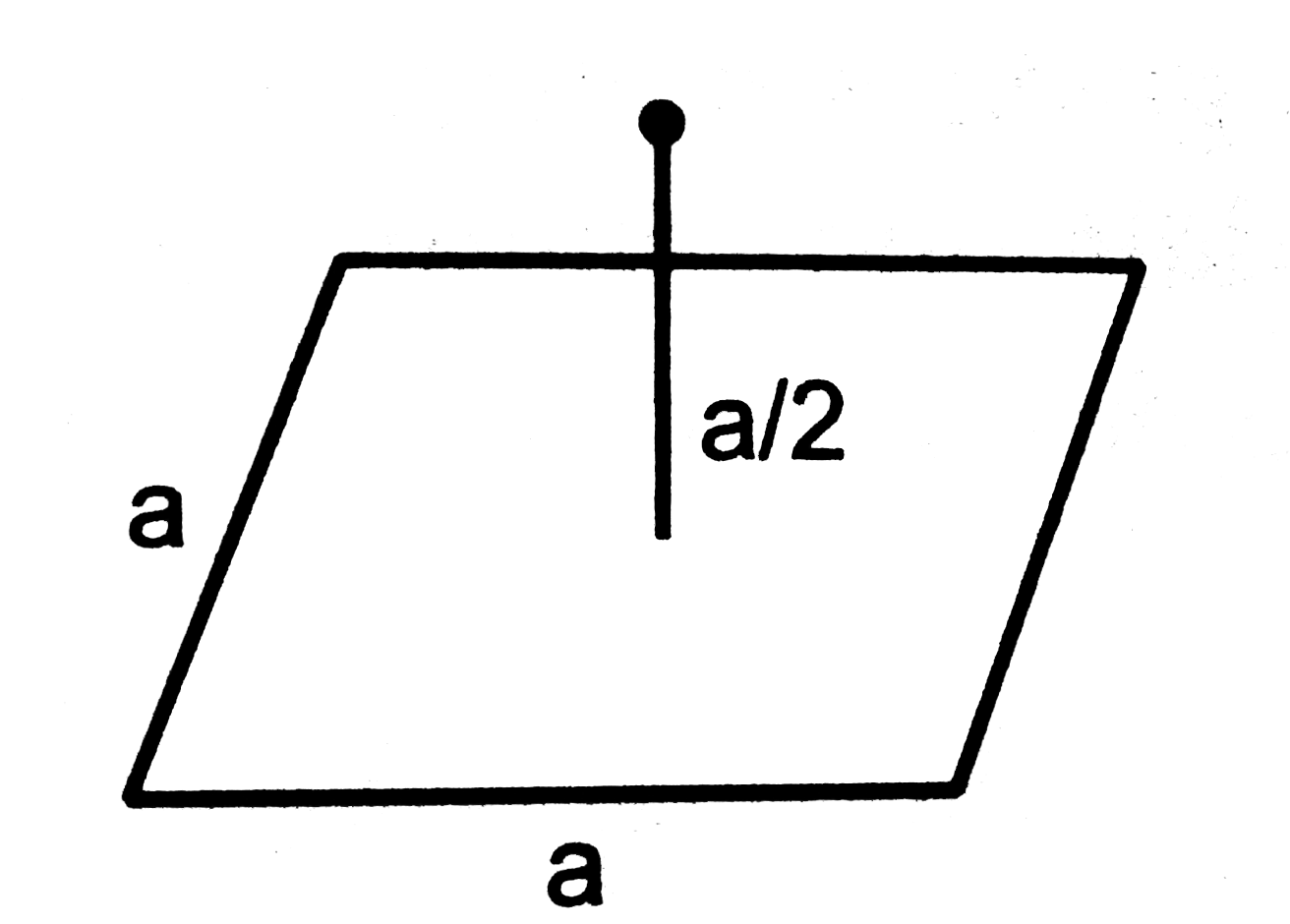 View Solution
View SolutionAs shown in Figure, charge Q is kept in the inner cavity and a charge of 2Q and 3Q are imparted to the inner and outermost shells.
(a) Find charge at each of the surface .
(b) Find E in the first annular region and outside.View Solution

