At a distance of 5cmand10cm outward from the surface of a uniformly charged solid sphere, the potentials are 100Vand75V, repectively. Then.
potential at its surface is 150V
the charge on the shre is 503×10−10C
the electric field on the surface is 1500V/m
the electric potential at its centre is 25V
The correct Answer is:A, B, C
To solve the problem, we need to find the radius of a uniformly charged solid sphere given the potentials at two points outside the sphere. We will denote the radius of the sphere as R and the charge on the sphere as Q.
1. Understanding the Problem:
We are given the potentials at distances of 5cm and 10cm from the surface of the sphere. Therefore, the distances from the center of the sphere are:
- Distance 1: r1=R+5cm
- Distance 2: r2=R+10cm
2. Using the Formula for Electric Potential:
The electric potential V at a distance r from the center of a uniformly charged sphere is given by:
V=kQr
where k is Coulomb's constant.
3. Setting Up the Equations:
From the problem, we have:
- At r1=R+5:
V1=kQR+5=100V
- At r2=R+10:
V2=kQR+10=75V
4. Dividing the Two Equations:
We can divide the two equations to eliminate kQ:
V1V2=kQR+5kQR+10⟹10075=R+10R+5
Simplifying gives:
43=R+10R+5
5. Cross Multiplying:
Cross-multiplying gives:
4(R+5)=3(R+10)
Expanding both sides:
4R+20=3R+30
6. Solving for R:
Rearranging the equation:
4R−3R=30−20⟹R=10cm
7. Conclusion:
The radius of the uniformly charged solid sphere is R=10cm.
We are given the potentials at distances of 5cm and 10cm from the surface of the sphere. Therefore, the distances from the center of the sphere are:
- Distance 1: r1=R+5cm
- Distance 2: r2=R+10cm
The electric potential V at a distance r from the center of a uniformly charged sphere is given by:
V=kQr
where k is Coulomb's constant.
From the problem, we have:
- At r1=R+5:
V1=kQR+5=100V
- At r2=R+10:
V2=kQR+10=75V
We can divide the two equations to eliminate kQ:
V1V2=kQR+5kQR+10⟹10075=R+10R+5
Simplifying gives:
43=R+10R+5
Cross-multiplying gives:
4(R+5)=3(R+10)
Expanding both sides:
4R+20=3R+30
Rearranging the equation:
4R−3R=30−20⟹R=10cm
The radius of the uniformly charged solid sphere is R=10cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
The electric field intensity at a distance 20cm from the centre of a uniformly charged non conducting solid sphere of radius 10cm is E.Then what is the electric field intensity at a distance 5cm from the centre it will be.....
View SolutionFlux (ph) as a function of distance (r) from centre of uniformly charged solid sphere of charge Q and radius R, is best represented by
View SolutionAt a point 20cm from the centre of a uniformly charged dielectric sphere of radius 10cm, the electric field is 100V/m. The electric field at 3cm from the centre of the sphere will be
View SolutionWhich graph best represents the variation of electric potential as a function of distance from the centre of a uniformly charged solid sphere of charge of radius R ?
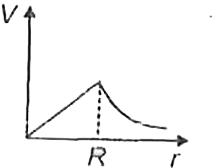 View Solution
View SolutionA spherical shell of radius 10 cm is carrying a charge q. If the electric potential at distances 5 cm, 10 cm and 15 cm from the centre of the spherical shell is V1,V2 and V3 respectively, then
View SolutionTwo conducting spheres of radii 3 cm and 1 m are separated by a distance of 10 cm in free space. If the spheres are charged to same potential of 10 V each, then the force of repulsion between them is
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.View SolutionTwo spherical conductors A and B of radii 1mm and 2mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is
View SolutionAn air bubble is seen inside a solid sphere of glass (n=1.5) of 4.0cm diameter at a distance of 1.0cm from the surface of the sphere (on seeing along the diameter). Determine the real position of the bubble inside the sphere.
View Solution

