A sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The value of distance rm at which electric field intensity is maximum is given by
rm=R3
rm=3R2
rm=2R3
rm=4R3
The correct Answer is:C
To find the distance rm at which the electric field intensity is maximum for a sphere with a volume charge density given by ρ=ρ0(1−rR), we can follow these steps:
Step 1: Determine the charge density
The charge density is given as:
ρ(r)=ρ0(1−rR)
This indicates that the charge density decreases linearly from ρ0 at the center of the sphere to 0 at the surface.
Step 2: Calculate the charge enclosed within a radius r
To find the electric field at a distance r from the center, we first need to find the total charge enclosed within a sphere of radius r:
Qenc=∫r0ρ(r′)dV
The volume element in spherical coordinates is dV=4πr′2dr′. Thus,
Qenc=∫r0ρ0(1−r′R)4πr′2dr′
Step 3: Evaluate the integral
Calculating the integral:
Qenc=4πρ0∫r0(1−r′R)r′2dr′
This can be split into two integrals:
=4πρ0(∫r0r′2dr′−1R∫r0r′3dr′)
Calculating these integrals:
∫r0r′2dr′=r33and∫r0r′3dr′=r44
Thus,
Qenc=4πρ0(r33−1R⋅r44)
=4πρ012r3−4πρ04Rr4
=4πρ012r3−πρ0Rr4
Step 4: Apply Gauss's Law to find the electric field
Using Gauss's Law, the electric field E(r) at a distance r is given by:
E(r)⋅4πr2=Qenc
Thus,
E(r)=Qenc4πr2
Substituting Qenc:
E(r)=14πϵ0(4πρ012r3−πρ0Rr4)⋅1r2
=ρ03ϵ0r−ρ04ϵ0Rr2
Step 5: Maximize the electric field
To find the maximum electric field, we differentiate E(r) with respect to r and set the derivative to zero:
dEdr=ρ03ϵ0−ρ02ϵ0Rr=0
Solving for r:
ρ03ϵ0=ρ02ϵ0Rr
r=2R3
Conclusion
Thus, the distance rm at which the electric field intensity is maximum is:
rm=2R3
The charge density is given as:
ρ(r)=ρ0(1−rR)
This indicates that the charge density decreases linearly from ρ0 at the center of the sphere to 0 at the surface.
To find the electric field at a distance r from the center, we first need to find the total charge enclosed within a sphere of radius r:
Qenc=∫r0ρ(r′)dV
The volume element in spherical coordinates is dV=4πr′2dr′. Thus,
Qenc=∫r0ρ0(1−r′R)4πr′2dr′
Calculating the integral:
Qenc=4πρ0∫r0(1−r′R)r′2dr′
This can be split into two integrals:
=4πρ0(∫r0r′2dr′−1R∫r0r′3dr′)
Calculating these integrals:
∫r0r′2dr′=r33and∫r0r′3dr′=r44
Thus,
Qenc=4πρ0(r33−1R⋅r44)
=4πρ012r3−4πρ04Rr4
=4πρ012r3−πρ0Rr4
Using Gauss's Law, the electric field E(r) at a distance r is given by:
E(r)⋅4πr2=Qenc
Thus,
E(r)=Qenc4πr2
Substituting Qenc:
E(r)=14πϵ0(4πρ012r3−πρ0Rr4)⋅1r2
=ρ03ϵ0r−ρ04ϵ0Rr2
To find the maximum electric field, we differentiate E(r) with respect to r and set the derivative to zero:
dEdr=ρ03ϵ0−ρ02ϵ0Rr=0
Solving for r:
ρ03ϵ0=ρ02ϵ0Rr
r=2R3
Thus, the distance rm at which the electric field intensity is maximum is:
rm=2R3
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.14videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.29videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
A sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity isView SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of electric field as a function of the distance r inside the sphere is given byView SolutionA sphere of charges of radius R carries a positive charge whose volume charge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), whereρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of the electric field as a functiion of the distance r outside the balll is given byView SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
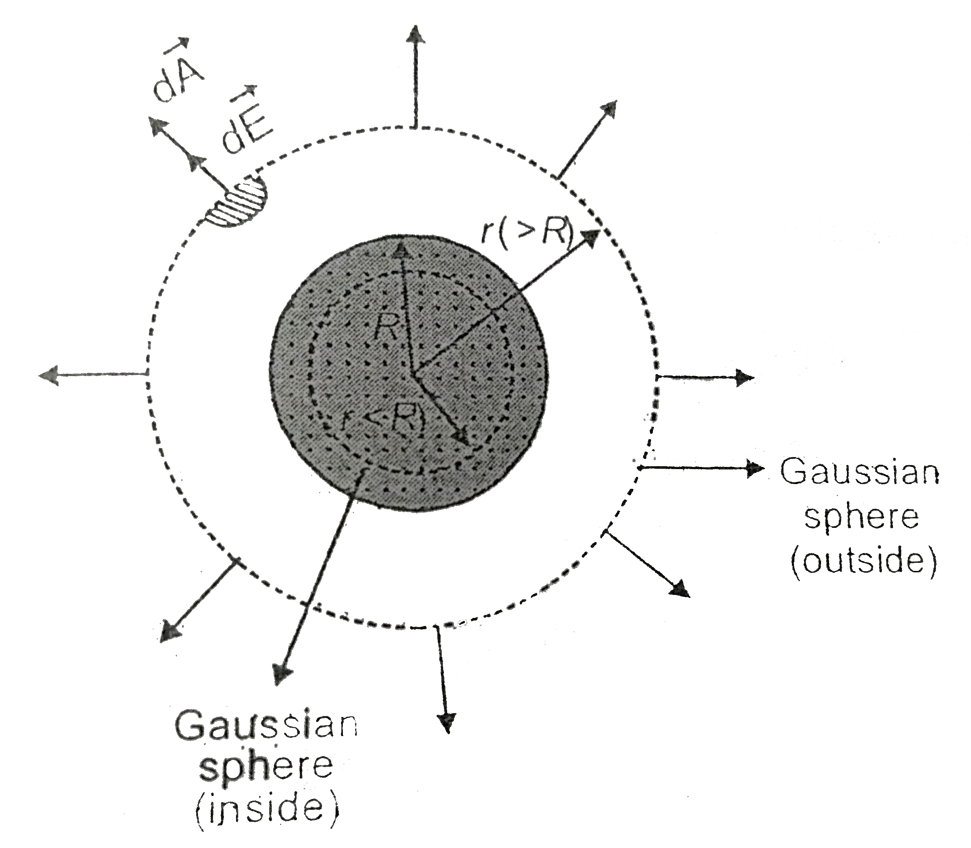
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]
 View Solution
View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionThe curve between charge density ρ and distance r near p−N junction will be
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View Solution

