The angular momentum of a particle about origin is varying as L =4t+8(SI units) whern its moves along a straight line y=x-4(x,y in metres). The magnitude of force acting on the particle will be
1 N
2 N
The correct Answer is:C
To solve the problem, we need to find the magnitude of the force acting on the particle given its angular momentum L and the path it follows. Let's break it down step by step.
Step 1: Understanding Angular Momentum
The angular momentum L of the particle about the origin is given by the equation:
L=4t+8
where t is time in seconds.
Step 2: Finding the Rate of Change of Angular Momentum
The torque τ is defined as the rate of change of angular momentum:
τ=dLdt
Calculating the derivative:
dLdt=ddt(4t+8)=4
Thus, the torque τ is:
τ=4N m
Step 3: Analyzing the Particle's Motion
The particle moves along the straight line given by the equation:
y=x−4
This can be rewritten in standard form:
y−x+4=0
The slope of this line is 1, which indicates that the angle θ with respect to the x-axis is:
tanθ=1⟹θ=45∘
Step 4: Relating Torque and Force
The relationship between torque, force, and the position vector r is given by:
τ=F⋅rsinθ
In this case, since θ=45∘:
τ=F⋅r⋅sin(45∘)
We know that sin(45∘)=1√2.
Step 5: Solving for Force
Rearranging the equation to solve for the magnitude of the force F:
F=τr⋅sin(45∘)
Substituting τ=4N m and sin(45∘)=1√2:
F=4r⋅1√2=4√2r
To find the magnitude of the force, we need the value of r.
Step 6: Finding the Position Vector r
The position vector r can be expressed in terms of x and y. For the line y=x−4, at any point (x,y):
r=√x2+(x−4)2=√x2+(x2−8x+16)=√2x2−8x+16
However, we can simplify our calculations by noting that we need the force magnitude, which is independent of r in this case.
Final Calculation
Since we are looking for the magnitude of the force, we can conclude that:
F=4√2 N
Conclusion
Thus, the magnitude of the force acting on the particle is:
4√2N
The angular momentum L of the particle about the origin is given by the equation:
L=4t+8
where t is time in seconds.
The torque τ is defined as the rate of change of angular momentum:
τ=dLdt
Calculating the derivative:
dLdt=ddt(4t+8)=4
Thus, the torque τ is:
τ=4N m
The particle moves along the straight line given by the equation:
y=x−4
This can be rewritten in standard form:
y−x+4=0
The slope of this line is 1, which indicates that the angle θ with respect to the x-axis is:
tanθ=1⟹θ=45∘
The relationship between torque, force, and the position vector r is given by:
τ=F⋅rsinθ
In this case, since θ=45∘:
τ=F⋅r⋅sin(45∘)
We know that sin(45∘)=1√2.
Rearranging the equation to solve for the magnitude of the force F:
F=τr⋅sin(45∘)
Substituting τ=4N m and sin(45∘)=1√2:
F=4r⋅1√2=4√2r
To find the magnitude of the force, we need the value of r.
The position vector r can be expressed in terms of x and y. For the line y=x−4, at any point (x,y):
r=√x2+(x−4)2=√x2+(x2−8x+16)=√2x2−8x+16
However, we can simplify our calculations by noting that we need the force magnitude, which is independent of r in this case.
Since we are looking for the magnitude of the force, we can conclude that:
F=4√2 N
Thus, the magnitude of the force acting on the particle is:
4√2N
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
40 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure
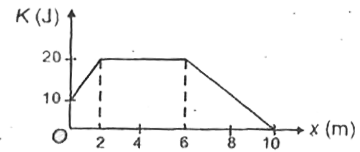
The magnitude of force acting on particle at x = 9 mis
View SolutionA particle moves along the straight line y=3x+5. Which coordinate changes at faster rate?
View SolutionA particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure
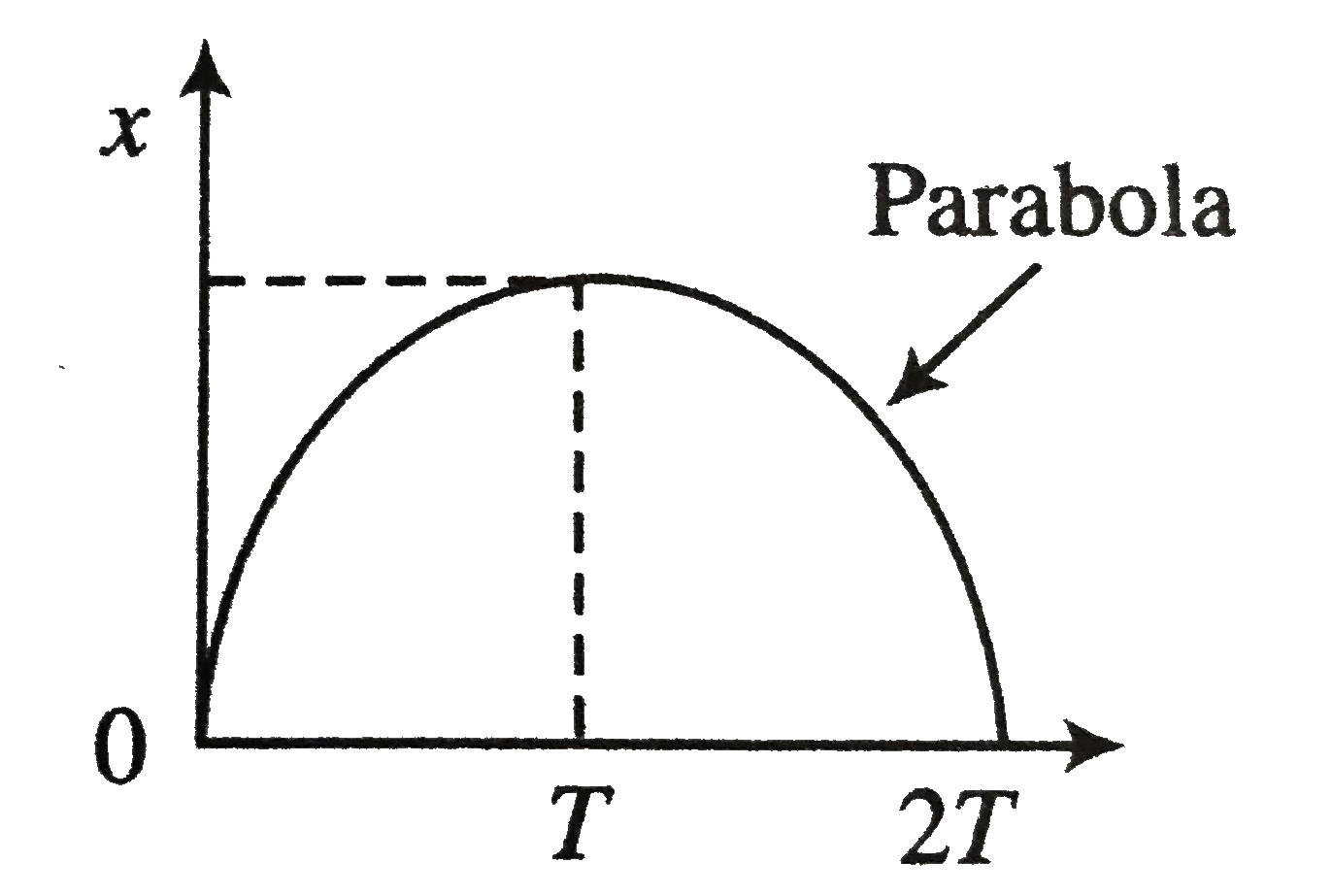
The a-t graph of the particle is correctly shown by
View SolutionThe distance traversed by a particle moving along a straight lne is given by x=180t+50t2 metre. The acceleration of the particle is
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View Solution
