Find the change in electric potential energy, ΔU as a charge of 2.20×10−6C, mass from a point A to point B, given that the change in electric potential between these points is ΔV=VB−VA=24.0V.
To find the change in electric potential energy (ΔU) when a charge moves from point A to point B, we can use the formula:
ΔU=Q⋅ΔV
where:
- ΔU is the change in electric potential energy,
- Q is the charge,
- ΔV is the change in electric potential.
1. Identify the given values:
- Charge, Q=2.20×10−6C
- Change in electric potential, ΔV=24.0V
2. Substitute the values into the formula:
ΔU=Q⋅ΔV
ΔU=(2.20×10−6C)⋅(24.0V)
3. Calculate the product:
- First, calculate 2.20×24.0:
2.20×24.0=52.8
- Now, include the exponent:
ΔU=52.8×10−6J
4. Express the result in scientific notation:
ΔU=5.28×10−5J
Final Answer:
ΔU=5.28×10−5J
- ΔU is the change in electric potential energy,
- Q is the charge,
- ΔV is the change in electric potential.
- Charge, Q=2.20×10−6C
- Change in electric potential, ΔV=24.0V
ΔU=Q⋅ΔV
ΔU=(2.20×10−6C)⋅(24.0V)
- First, calculate 2.20×24.0:
2.20×24.0=52.8
- Now, include the exponent:
ΔU=52.8×10−6J
ΔU=5.28×10−5J
ΔU=5.28×10−5J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Find the change in electric potential energy , ΔU as a charge of (a) 2.20×10−6C. (b) −1.10×10−6C moves from a point A to a point given that the change in electric potential between these points is ΔV=VB−VA=24.0V
View SolutionIn, a potential of +12V is given to point A, and point B is earthed. What is the potential at the point P in V?
 .
.
View SolutionThe work done in carrying a charge of 5μC form a point A to a point B in an electric field is 10mJ. The potential difference (VB−VA) is then
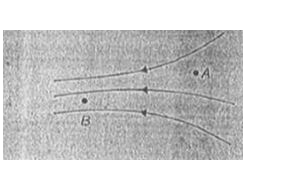
View SolutionIn figure two points A and B are located in a region of electric field . The potential difference VB−VA is
View SolutionHow much work will be done in bringing a charge of 400μC from infinity to some point P in the region of electric field ? Given that the electric potential at point P is 20 V ?
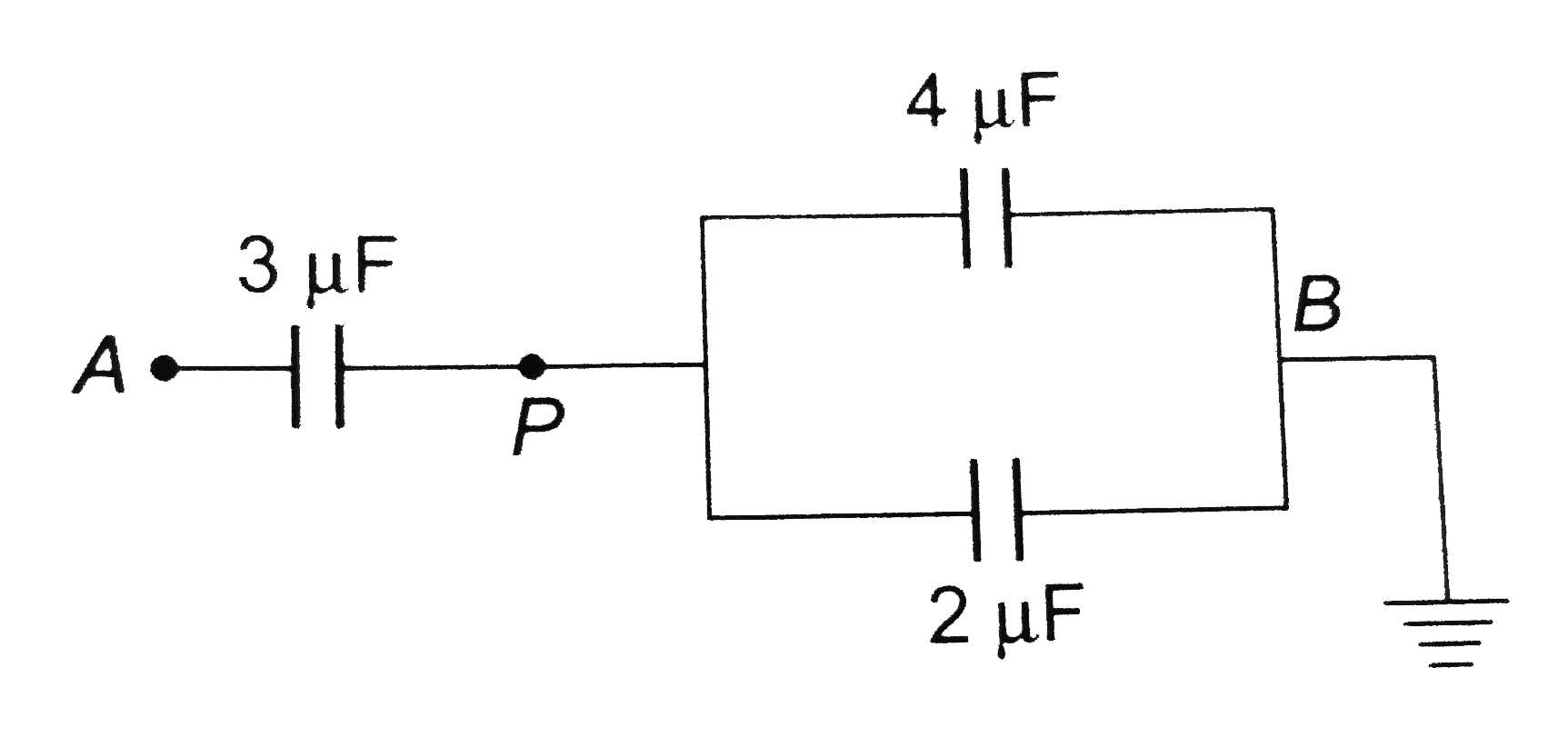
View SolutionIn the figure a potential of +1200V is given to point A and point B is earthed, what is the potential at the point P ?
View SolutionThe kinetc energy of a chargd particle decreased by 10 J as it moves from a point at potential 100 V to a point at potential 200V . Find the charge on the particle.
View SolutionOn moving a charge of 2C from a point A where potential is +12V to a point B where potential is -12 V, the work done is -
View SolutionIf V and u are electric potential and energy density, respectively, at a distance r from a positive point charge, then which of the following graph is correct ?
View SolutionA point charge q1 is held stationary at the origin. A second charge q2 is placed at a point a, and the electric potential energy of the pair of charges is −6.4×10−8J. When the second charge is moved to point b, the electric force on the charge does 4.2×10−8J of work. What is the electric potential energy of the pair of charges when the second charge is at point b?
View Solution
