Equipotentials at a great distance from a collection of charges whose total sum is not zero are approximately
spheres
planes
paraboloids
ellipsoids
The correct Answer is:A
To solve the question regarding the equipotential surfaces at a great distance from a collection of charges whose total sum is not zero, we can follow these steps:
1. Understanding Equipotential Surfaces:
Equipotential surfaces are those surfaces where the electric potential is the same at every point. This means that no work is done when moving a charge along these surfaces.
2. Considering a Collection of Charges:
When we have a collection of charges, if the total charge is not zero, the electric field will be present at a distance from these charges. The behavior of the electric field and potential at a distance from the charges can be analyzed.
3. Point Charge Approximation:
At a great distance from a collection of charges, we can approximate the entire collection as a single point charge. This is due to the fact that the electric field decreases with the square of the distance from the charge.
4. Electric Potential Due to a Point Charge:
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant. As r increases, the potential V decreases.
5. Equipotential Surfaces at a Distance:
At a distance r from the charge, the potential remains constant for all points that are equidistant from the charge. Thus, the equipotential surfaces around a point charge are spherical surfaces centered around the charge.
6. Conclusion:
Therefore, at a great distance from a collection of charges whose total sum is not zero, the equipotential surfaces can be approximated as spherical surfaces. This means that the correct answer to the question is that the equipotential surfaces are approximately spherical.
Final Answer:
The equipotential surfaces at a great distance from a collection of charges whose total sum is not zero are approximately spherical.
Equipotential surfaces are those surfaces where the electric potential is the same at every point. This means that no work is done when moving a charge along these surfaces.
When we have a collection of charges, if the total charge is not zero, the electric field will be present at a distance from these charges. The behavior of the electric field and potential at a distance from the charges can be analyzed.
At a great distance from a collection of charges, we can approximate the entire collection as a single point charge. This is due to the fact that the electric field decreases with the square of the distance from the charge.
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant. As r increases, the potential V decreases.
At a distance r from the charge, the potential remains constant for all points that are equidistant from the charge. Thus, the equipotential surfaces around a point charge are spherical surfaces centered around the charge.
Therefore, at a great distance from a collection of charges whose total sum is not zero, the equipotential surfaces can be approximated as spherical surfaces. This means that the correct answer to the question is that the equipotential surfaces are approximately spherical.
The equipotential surfaces at a great distance from a collection of charges whose total sum is not zero are approximately spherical.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential ϕ at that point is
AWQxBWCWxDWQ
A solid sphere of radius R has total charge 2Q and volume charge density p=kr where r is distance from centre. Now charges Q and −Q are placed diametrically opposite at distance 2a where a is distance form centre of sphere such that net force on charge Q is zero then relation between a and R is
View SolutionA particle of mass m carrying charge q is projected with velocity v from point P toward aninfinite line of charge from a distance a . Its speed reduces to zero momentarily at point Q, which is at a distance a/2 from the line of charge. If another particle with mass m and charge −q is projected with the same velosity v from P toward the line of charge, what will be its speed at Q ?
View SolutionThe magnitude of electric intensity at a distance x from a charge q is E.An identical charge is placed at a distance 2x from it Then the magnitude of the force it experience is ..
View SolutionEquipotential spheres are drawn round a point charge. As we move away from charge will the spacing between two spheres having a constant potential difference decrease, increase or remain constant.
View SolutionEquipotential spheres are drawn round a point charge. As we move away from charge will the spacing between two spheres having a constant potential difference decrease, increase or remain constant.
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionA square of side d, made from a thin insulating plate, is uniformly charged and carries a total charge of Q. A point charge q is placed on the symmetrical normal axis of the square at a distance d/2 from the plate. How large is the force acting on the point charge ?
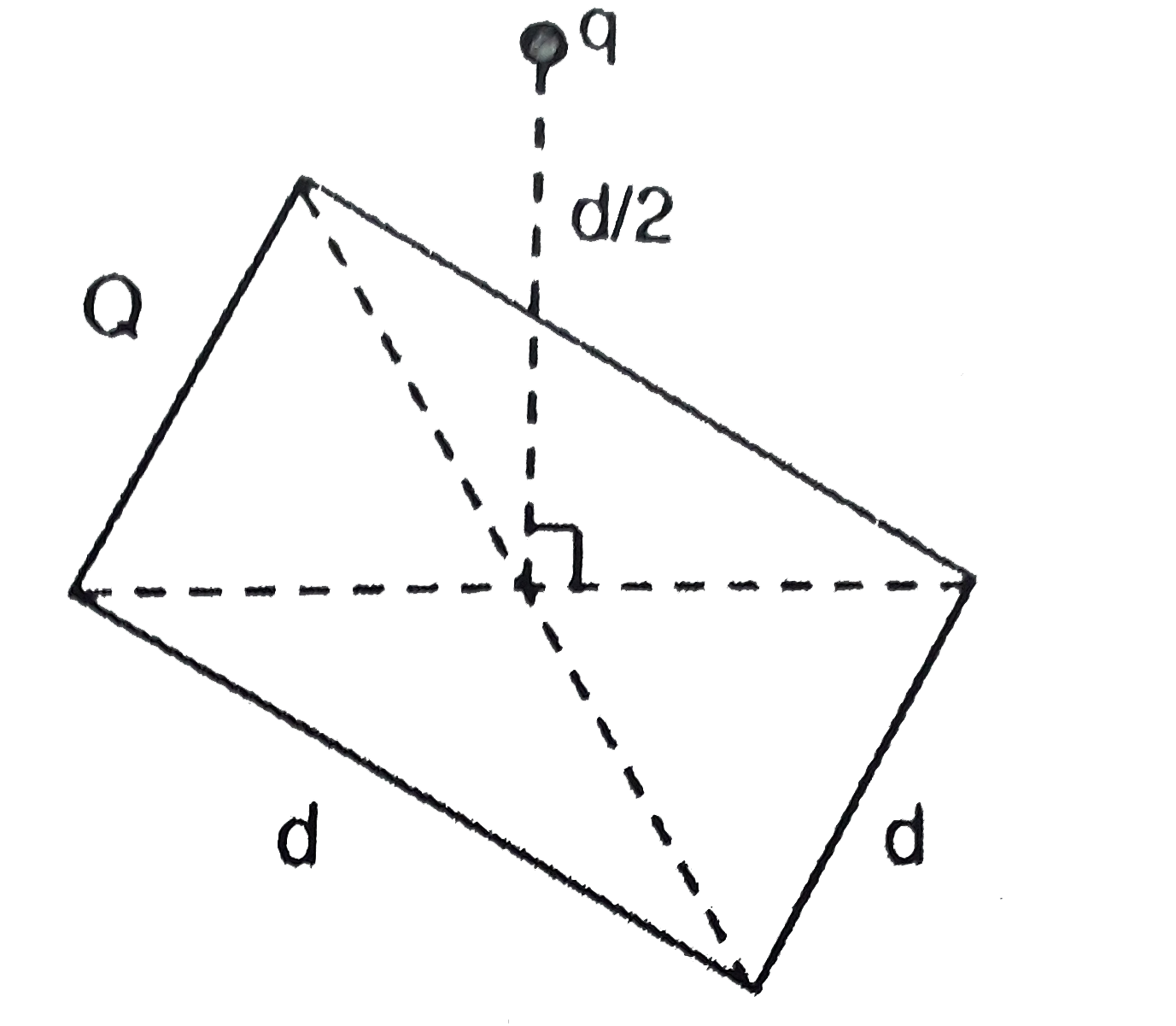
View Solution
