The capacitance of the earth, viewed as a spherical conductor of radius 6408 km is
980μF
1424μF
712μF
356μF
The correct Answer is:C
To find the capacitance of the Earth viewed as a spherical conductor, we can follow these steps:
Step 1: Understand the formula for capacitance
The capacitance C of a spherical conductor can be expressed using the formula:
C=QV
where Q is the charge on the conductor and V is the potential of the conductor.
Step 2: Determine the potential V
For a spherical conductor, the potential V at its surface due to a charge Q is given by:
V=kQR
where k is Coulomb's constant (k=14πϵ0), and R is the radius of the sphere.
Step 3: Set up the equation for capacitance
Since the Earth is isolated, we can set the potential V at infinity to zero. Therefore, the potential difference becomes:
V=kQR−0=kQR
Substituting this into the capacitance formula gives:
C=QkQR=Rk
Step 4: Substitute the values
Given that the radius R of the Earth is 6408 km, we convert this to meters:
R=6408×103m
Now, we need to substitute the value of k:
k=9×109N m2/C2
Thus, the capacitance C becomes:
C=6408×1039×109
Step 5: Calculate the capacitance
Now, we perform the calculation:
C=6408×1039×109=64089×10−6F
Calculating 64089:
C≈712×10−6F
This can also be expressed in microfarads:
C≈712μF
Final Answer
The capacitance of the Earth viewed as a spherical conductor is approximately 712μF.
---
The capacitance C of a spherical conductor can be expressed using the formula:
C=QV
where Q is the charge on the conductor and V is the potential of the conductor.
For a spherical conductor, the potential V at its surface due to a charge Q is given by:
V=kQR
where k is Coulomb's constant (k=14πϵ0), and R is the radius of the sphere.
Since the Earth is isolated, we can set the potential V at infinity to zero. Therefore, the potential difference becomes:
V=kQR−0=kQR
Substituting this into the capacitance formula gives:
C=QkQR=Rk
Given that the radius R of the Earth is 6408 km, we convert this to meters:
R=6408×103m
Now, we need to substitute the value of k:
k=9×109N m2/C2
Thus, the capacitance C becomes:
C=6408×1039×109
Now, we perform the calculation:
C=6408×1039×109=64089×10−6F
Calculating 64089:
C≈712×10−6F
This can also be expressed in microfarads:
C≈712μF
The capacitance of the Earth viewed as a spherical conductor is approximately 712μF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The capacitance of earth, treating it as a spherical conductor of radius 6400 km is
View SolutionThe capacity of a spherical conductor is
View SolutionThe electric field strength in air at NTP is 3×106V/m. The maximum charge that can be given to a spherical conductor of radius 3m is
View SolutionWhich one of the following graphs represents the variation of electric field with distance r from the centre of a charged spherical conductor of radius R?
View SolutionCapacitance (in F) of a spherical conductor with radius 1m is
View SolutionThe number of electrons to be put on a spherical conductor of radius 0.1m to produce an electric field of 0.036N/C just above its surface is
View SolutionThe number of electrons to be put on a spherical conductor of radius 0.1m to produce an electric field of 0.036N/C just above its surface is
View SolutionFind the electrostatic force of interaction between two halves of a spherical conductor of radius R carrying a charge Q.
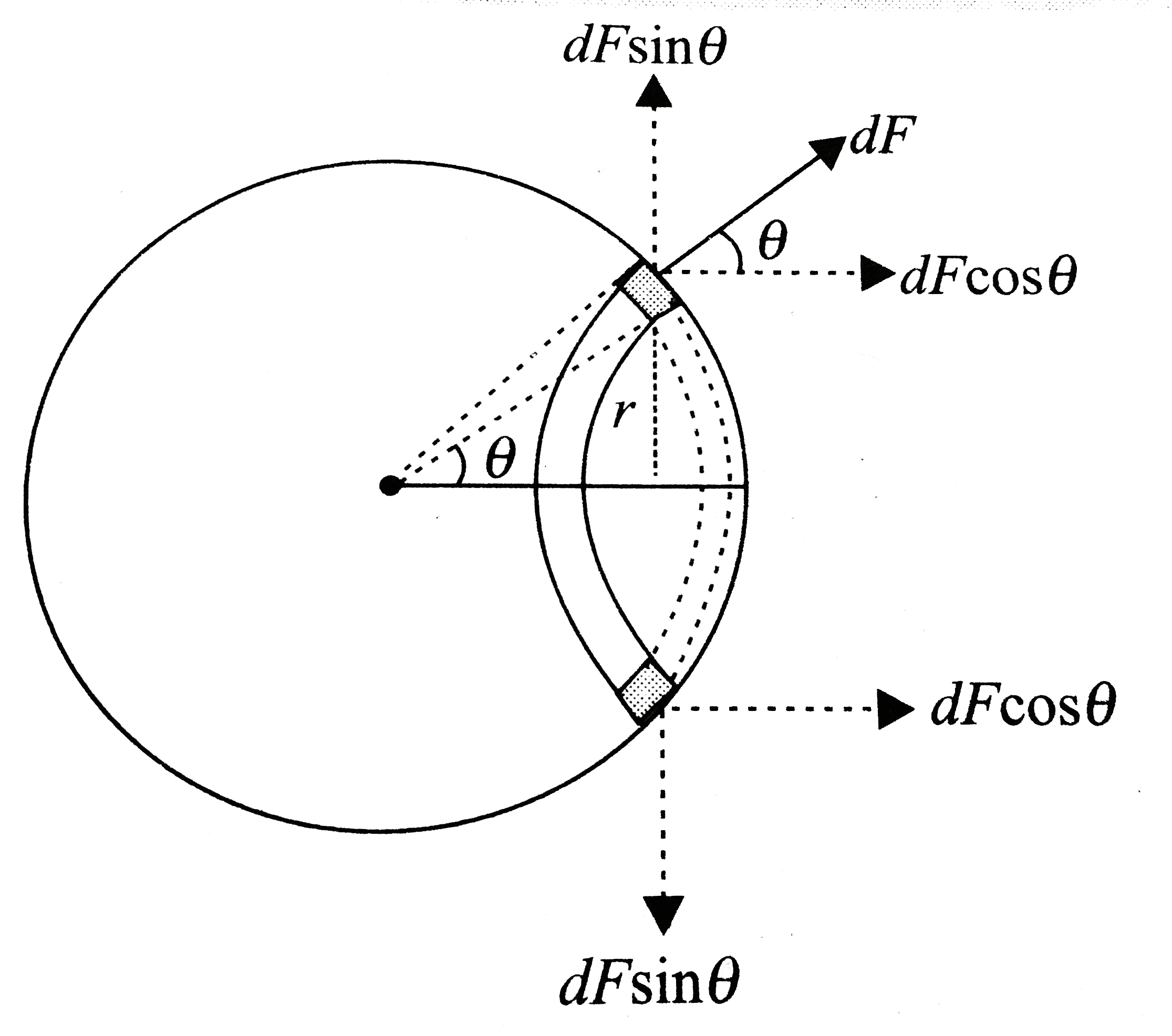
View SolutionA spherical conductor of radius 2m is charged to a potential of 120V. It is now placed inside another hollow spherical conductor of radius 6m. Calculate the potential to which the bigger sphere would be raised
View SolutionA spherical conductor of radius 2 m is charged to a potential of 120 V. It is now placed inside another hollow spherical conductor of radius 6 m. calculate the potential of bigger sphere, if the smaller sphere is made to touch the bigger sphere
View Solution
