The resistor of resistance ' R ' is connected to 25 V supply and heat produced in it is 25 J / sec. The value of R is
225Ω
1Ω
25Ω
50Ω
The correct Answer is:C
To solve the problem, we need to find the resistance R given that a resistor connected to a 25 V supply produces heat at a rate of 25 J/s (which is equivalent to 25 W).
1. Understanding the Problem:
We know that the power P dissipated in a resistor due to heat is given by Joule's law, which states:
P=I2R
where P is the power in watts (W), I is the current in amperes (A), and R is the resistance in ohms (Ω).
2. Given Values:
- Voltage V=25V
- Power P=25W
3. Using Ohm's Law:
According to Ohm's law, the relationship between voltage, current, and resistance is given by:
V=IR
From this, we can express current I in terms of voltage and resistance:
I=VR
4. Substituting into the Power Equation:
Now, substitute I from Ohm's law into the power equation:
P=(VR)2R
Simplifying this gives:
P=V2R
5. Rearranging to Find Resistance:
We can rearrange the equation to solve for R:
R=V2P
6. Substituting the Known Values:
Now substitute the known values of V and P:
R=25225
R=62525
R=25Ω
7. Conclusion:
Therefore, the value of the resistance R is 25Ω.
We know that the power P dissipated in a resistor due to heat is given by Joule's law, which states:
P=I2R
where P is the power in watts (W), I is the current in amperes (A), and R is the resistance in ohms (Ω).
- Voltage V=25V
- Power P=25W
According to Ohm's law, the relationship between voltage, current, and resistance is given by:
V=IR
From this, we can express current I in terms of voltage and resistance:
I=VR
Now, substitute I from Ohm's law into the power equation:
P=(VR)2R
Simplifying this gives:
P=V2R
We can rearrange the equation to solve for R:
R=V2P
Now substitute the known values of V and P:
R=25225
R=62525
R=25Ω
Therefore, the value of the resistance R is 25Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A resistor of resistance R is connected to a cell internal resistance 5Ω. The value of R is varied from 1Ω to 5Ω. The power consumed by R
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View SolutionA filament bulb (500W,100V) is to be used in a 230V main supply. When a resistance R is connected in series, it works perfectly and the bulb consumers 500W. The value of R is
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
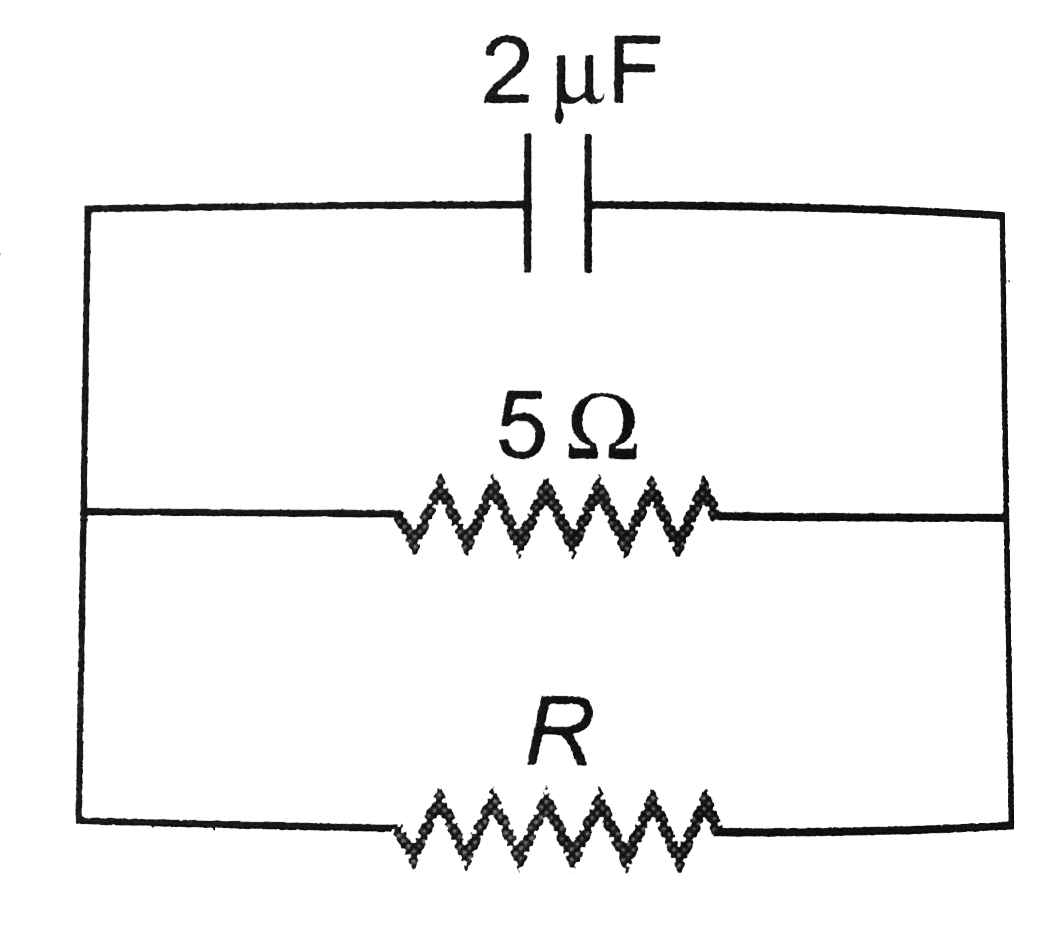
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to

View SolutionIn the figure shown eight resistors eachof resistance 'R' are connected to form two squares ABCH and DEFG. Four resistors each of resistors '2R' are connected in the vertical lines AF, BG, CD and EH. 'A' and 'C' are connected to a battery of interal resistance 'R' and emf V. Find out the current in 'AB' and 'ED'.

View SolutionWhat will be the motion of the conductor of the previous problem, if a resistor of resistance R is connected into the circuit instead of the capacitor? Neglect the resistance of the conductors.
View SolutionIf i=0.25 amp. In fig then value of R is:-
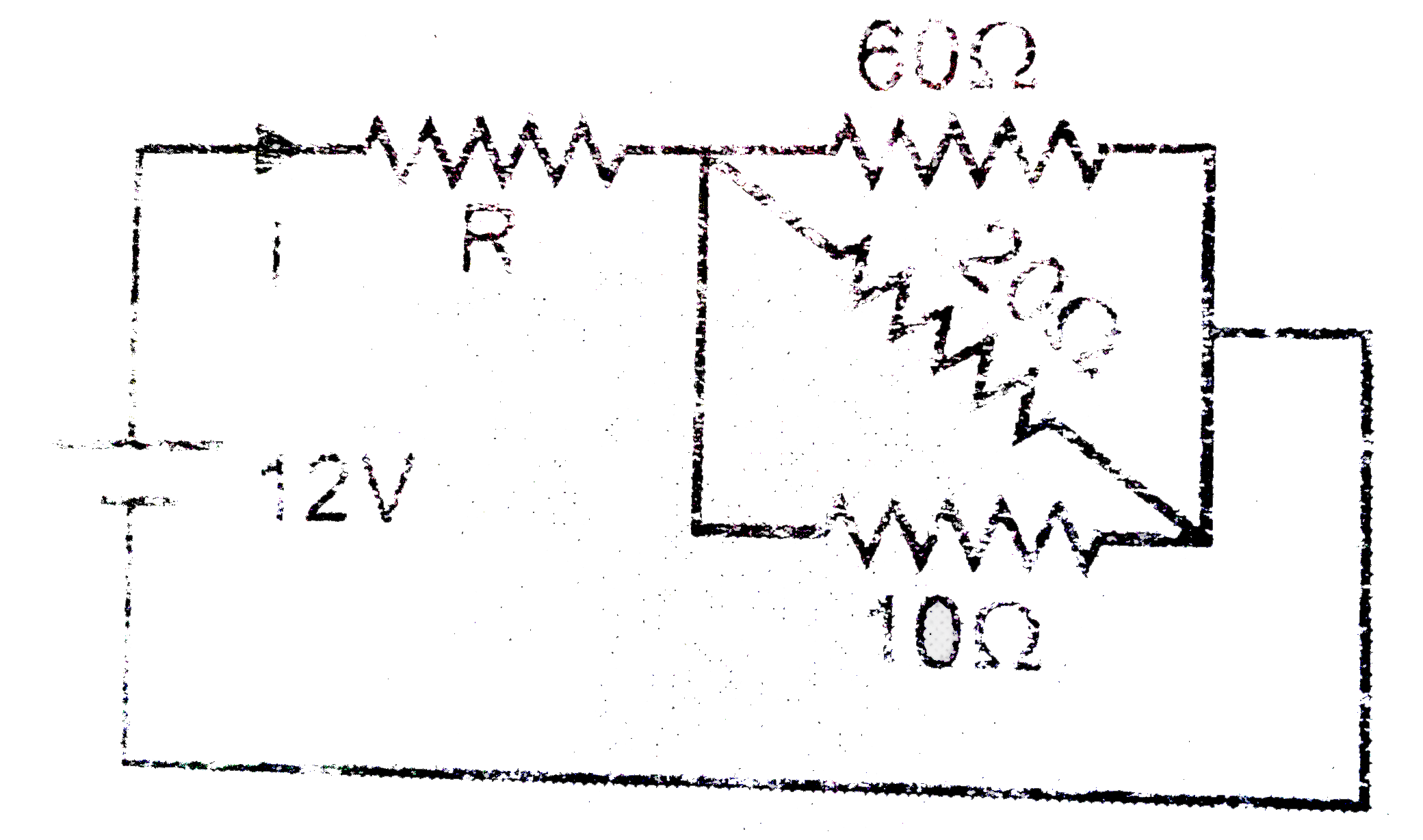
View Solution
