A resistance of 1980Ω is connected in series with a voltmeter, after which the scale division becomes 100 times larger. Find the resistance of voltmeter.
10Ω
20Ω
30Ω
40Ω
The correct Answer is:B
To solve the problem, we need to find the resistance of the voltmeter when a resistance of 1980 Ω is connected in series with it, causing the scale division to become 100 times larger.
1. Understanding the Initial Setup:
- Let Rv be the resistance of the voltmeter.
- Initially, the voltage across each division of the voltmeter is given by V=IG⋅Rv/n, where IG is the current through the voltmeter and n is the number of divisions.
2. Connecting the Resistance in Series:
- When a resistance of 1980 Ω is connected in series with the voltmeter, the total resistance becomes Rv+1980.
- The new voltage across each division now becomes V′=IG⋅(Rv+1980)/n.
3. Relating the Two Voltages:
- According to the problem, the new voltage across each division is 100 times the initial voltage:
V′=100⋅V
- Substituting the expressions for V and V′:
IG⋅(Rv+1980)n=100⋅IG⋅Rvn
- We can cancel IG/n from both sides (assuming IG is not zero):
Rv+1980=100⋅Rv
4. Rearranging the Equation:
- Rearranging the equation gives:
1980=100Rv−Rv
1980=99Rv
5. Solving for Rv:
- Dividing both sides by 99:
Rv=198099=20Ω
Final Answer:
The resistance of the voltmeter Rv is 20 Ω.
- Let Rv be the resistance of the voltmeter.
- Initially, the voltage across each division of the voltmeter is given by V=IG⋅Rv/n, where IG is the current through the voltmeter and n is the number of divisions.
- When a resistance of 1980 Ω is connected in series with the voltmeter, the total resistance becomes Rv+1980.
- The new voltage across each division now becomes V′=IG⋅(Rv+1980)/n.
- According to the problem, the new voltage across each division is 100 times the initial voltage:
V′=100⋅V
- Substituting the expressions for V and V′:
IG⋅(Rv+1980)n=100⋅IG⋅Rvn
- We can cancel IG/n from both sides (assuming IG is not zero):
Rv+1980=100⋅Rv
- Rearranging the equation gives:
1980=100Rv−Rv
1980=99Rv
- Dividing both sides by 99:
Rv=198099=20Ω
The resistance of the voltmeter Rv is 20 Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example
65 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View Solution(a) Briefly explain how a galvanometer is converted into a voltmeter.
(b) A voltmeter of a certain range is constructed by connecting a resistance of 980Ω in series with a galvanometer. When the resistance of 470Ω is connected in series, the range gets halved. Find the resistance of the galvanometer.
View Solution
Knowledge Check
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800
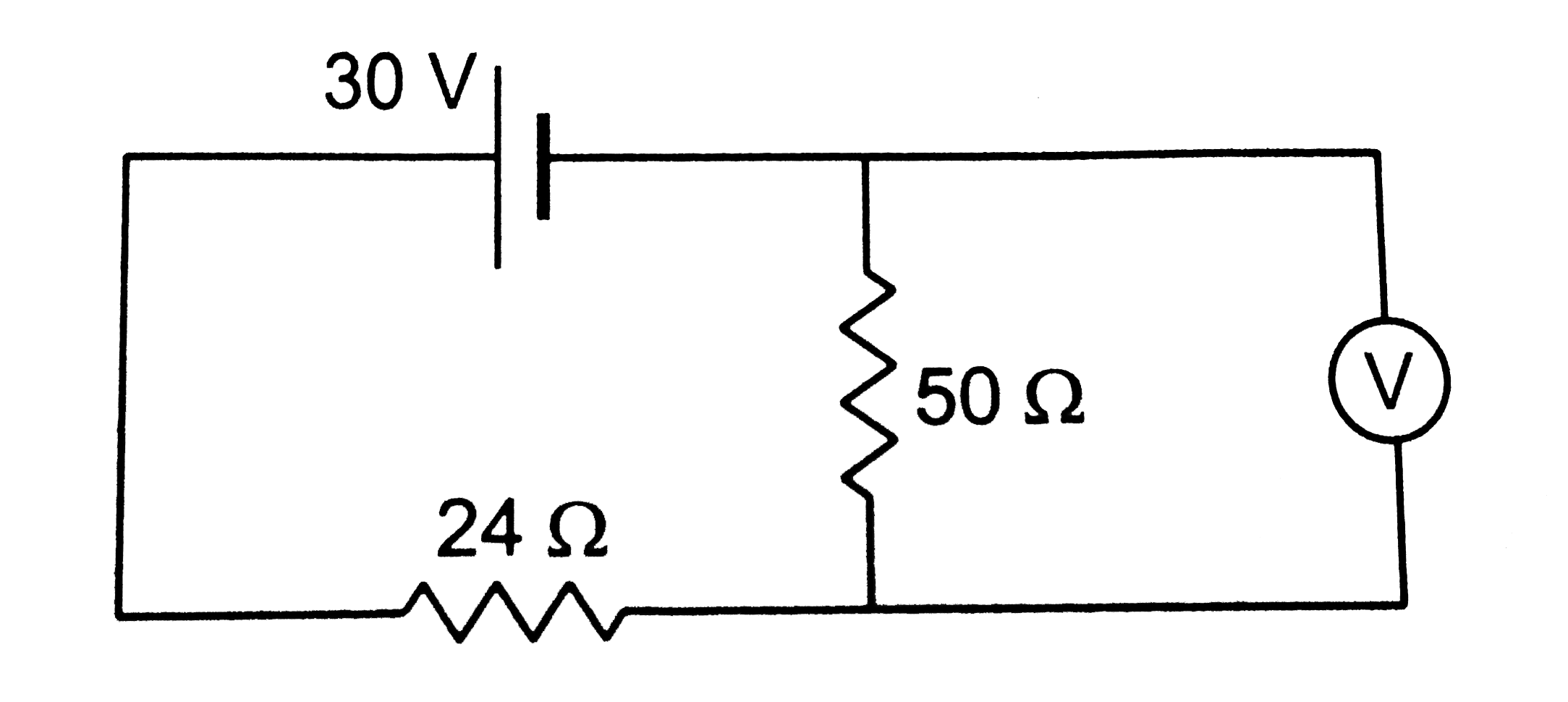
The voltmeter shown in figure reads 18V across the 50(Ω)resistor. Find the resistance of the voltmeter.
View SolutionAn ammeter and a voltmeter are connected in series to a battery with an emf ξ=6.0V. When a certain resistance is connected in parallel with the voltmeter, the readings of the latter decreases η=2.0 times, whereas the readings of the ammeter increase the same number of times, Find the voltmeter readings after the connection of the resistance.
View SolutionThe voltmeter shown in the figure reads 10V across 40 ω . The resistance of voltmeter is
View SolutionTwo resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
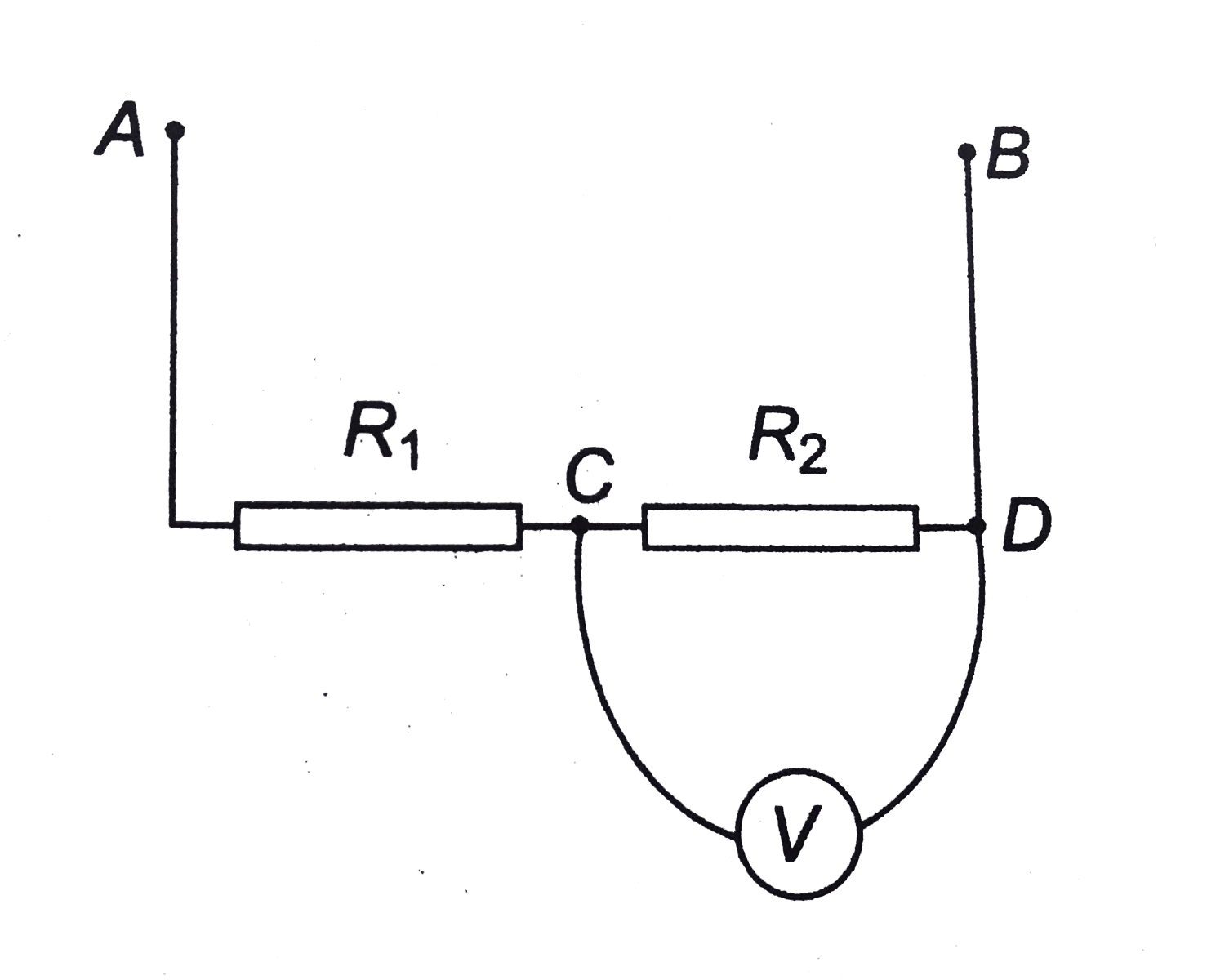
View SolutionResistance R1and R2, each 60Ω, are connected in series. The Potential difference between points A and B is 120V. Find the reading of voltmeter connected resistance r=120Ω
View SolutionResistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View Solution
