A battery of four cells in series, each having an emf of 1.14 V and an internal resistance of 2Ω is to be used to charge a small 2 V accumulator of negligible internal resistance. What is the charging current?
0.1A
0.2A
0.3A
0.45A
The correct Answer is:C
To find the charging current from a battery of four cells in series, we can follow these steps:
Step 1: Determine the total EMF of the battery
Each cell has an EMF of 1.14V, and there are 4 cells in series. The total EMF (E) can be calculated as:
\(
E = n \times \text{EMF of each cell} = 4 \times 1.14 \, \text{V} = 4.56 \, \text{V}
\)
Step 2: Determine the total internal resistance of the battery
Each cell has an internal resistance of 2Ω. Since they are in series, the total internal resistance (R) is:
\(
R = n \times \text{internal resistance of each cell} = 4 \times 2 \, \Omega = 8 \, \Omega
\)
Step 3: Set up the equation using Kirchhoff's Voltage Law (KVL)
When charging the 2 V accumulator, we can apply KVL around the loop. The equation can be set up as follows:
\(
E - V - I \cdot R = 0
\)
Where:
- \( E = 4.56 \, \text{V} \) (total EMF)
- \( V = 2 \, \text{V} \) (voltage across the accumulator)
- \( R = 8 \, \Omega \) (total internal resistance)
- \( I \) is the charging current we need to find.
Rearranging the equation gives:
\(
4.56 \, \text{V} - 2 \, \text{V} - I \cdot 8 \, \Omega = 0
\)
\(
2.56 \, \text{V} = I \cdot 8 \, \Omega
\)
Step 4: Solve for the charging current (I)
Now, we can solve for \( I \):
\(
I = \frac{2.56 \, \text{V}}{8 \, \Omega} = 0.32 \, \text{A}
\)
Conclusion
The charging current is:
\(
I = 0.32 \, \text{A}
\)
Each cell has an EMF of 1.14V, and there are 4 cells in series. The total EMF (E) can be calculated as:
\(
E = n \times \text{EMF of each cell} = 4 \times 1.14 \, \text{V} = 4.56 \, \text{V}
\)
Each cell has an internal resistance of 2Ω. Since they are in series, the total internal resistance (R) is:
\(
R = n \times \text{internal resistance of each cell} = 4 \times 2 \, \Omega = 8 \, \Omega
\)
When charging the 2 V accumulator, we can apply KVL around the loop. The equation can be set up as follows:
\(
E - V - I \cdot R = 0
\)
Where:
- \( E = 4.56 \, \text{V} \) (total EMF)
- \( V = 2 \, \text{V} \) (voltage across the accumulator)
- \( R = 8 \, \Omega \) (total internal resistance)
- \( I \) is the charging current we need to find.
\(
4.56 \, \text{V} - 2 \, \text{V} - I \cdot 8 \, \Omega = 0
\)
\(
2.56 \, \text{V} = I \cdot 8 \, \Omega
\)
Now, we can solve for \( I \):
\(
I = \frac{2.56 \, \text{V}}{8 \, \Omega} = 0.32 \, \text{A}
\)
The charging current is:
\(
I = 0.32 \, \text{A}
\)
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Maximum current produced by a cell of emf 10 V and internal resistance 2Ω is
View SolutionA battery of six cells each of e.m.f. 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω what will be the charging current.
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionA battery of 20 cells (each having e.m.f. 1.8V and internal resistance 0.1Ω is charged by 220 volts and the charging current is 15A. Calculate the resistance to be put in the circuit.
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View SolutionA series battery of six cells each of emf2V and internal resistance 0.5Ω is charged by a 100Vdc supply. What resistance should be used in the charging circuit in order to limit the charging current to 8A. Using this relation , obtain (a) the powwer supplied by the dc source, (b) the power dissipated as heat , and (c) the chemical energy stored in the battery in 15min.
View Solutionin the circuit shown in the figure, each battery is of 5 V and has an internal resistance of 0.2 Omega What is the reading of the ideal voltmeter V
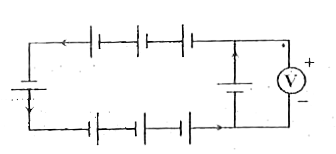
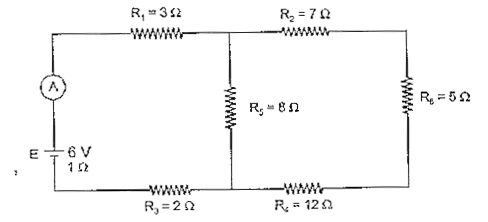
View SolutionIn the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
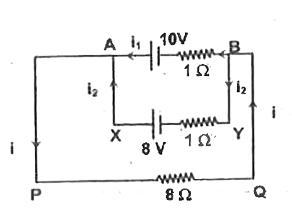
View Solution
