Three unequal resistor in parallel are equivalent to a resistance ohm If two of them are in the ratio and if no resistance value is fractional the largest of three resistance in ohm is
4
6
8
12
The correct Answer is:B
To solve the problem, we need to find the largest of three unequal resistors in parallel, given that their equivalent resistance is 1 ohm and two of them are in the ratio of 1:2. Let's denote the resistances as R1, R2, and R3.
1. Assign Variables Based on the Ratio:
Since R1 and R2 are in the ratio of 1:2, we can express them as:
R1=xandR2=2x
where x is a positive integer.
2. Use the Formula for Equivalent Resistance in Parallel:
The formula for the equivalent resistance Req of resistors in parallel is given by:
1Req=1R1+1R2+1R3
Substituting the values we have:
11=1x+12x+1R3
3. Combine the Terms:
To combine the fractions on the right-hand side, we need a common denominator. The common denominator for x and 2x is 2x:
1=22x+12x+1R3
This simplifies to:
1=32x+1R3
4. Rearrange the Equation:
Rearranging the equation gives:
1−32x=1R3
Taking the reciprocal:
R3=11−32x=2x2x−3
5. Ensure No Fractional Values:
Since all resistance values must be integers and not fractional, the expression 2x−3 must divide 2x evenly. This means 2x−3 must be a factor of 2x.
6. Set Conditions for Integer Values:
For R3 to be an integer, 2x−3 must be a divisor of 2x. Therefore, we can set:
2x - 3 = k \quad \text{(where k is an integer)}
Rearranging gives:
2x=k+3⇒x=k+32
For x to be an integer, k+3 must be even, which implies k must be odd.
7. Finding Possible Values:
Testing integer values for k:
- If k=1: x=2, then R1=2, R2=4, R3=41=4 (not unequal).
- If k=3: x=3, then R1=3, R2=6, R3=63=2 (unequal).
- If k=5: x=4, then R1=4, R2=8, R3=85=1.6 (not integer).
8. Conclusion:
The only valid case that satisfies all conditions is when x=3:
R1=3ohm,R2=6ohm,R3=2ohm
Thus, the largest resistance is:
Largest Resistance=R2=6ohm
Final Answer:
The largest of the three resistances is 6 ohms.
Since R1 and R2 are in the ratio of 1:2, we can express them as:
R1=xandR2=2x
where x is a positive integer.
The formula for the equivalent resistance Req of resistors in parallel is given by:
1Req=1R1+1R2+1R3
Substituting the values we have:
11=1x+12x+1R3
To combine the fractions on the right-hand side, we need a common denominator. The common denominator for x and 2x is 2x:
1=22x+12x+1R3
This simplifies to:
1=32x+1R3
Rearranging the equation gives:
1−32x=1R3
Taking the reciprocal:
R3=11−32x=2x2x−3
Since all resistance values must be integers and not fractional, the expression 2x−3 must divide 2x evenly. This means 2x−3 must be a factor of 2x.
For R3 to be an integer, 2x−3 must be a divisor of 2x. Therefore, we can set:
2x - 3 = k \quad \text{(where k is an integer)}
Rearranging gives:
2x=k+3⇒x=k+32
For x to be an integer, k+3 must be even, which implies k must be odd.
Testing integer values for k:
- If k=1: x=2, then R1=2, R2=4, R3=41=4 (not unequal).
- If k=3: x=3, then R1=3, R2=6, R3=63=2 (unequal).
- If k=5: x=4, then R1=4, R2=8, R3=85=1.6 (not integer).
The only valid case that satisfies all conditions is when x=3:
R1=3ohm,R2=6ohm,R3=2ohm
Thus, the largest resistance is:
Largest Resistance=R2=6ohm
The largest of the three resistances is 6 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The equivalent resistance of two resistor connected in series is 6Ω and their equivalent resistance is 43Ω. What are the values of resistances ?
View SolutionResistance n, each of rohm, when connected in parallel give an equivalent resistance of Rohm. If these resistances were connected series, the combination would have a resistance in ohm, equal to
View Solution
Knowledge Check
Equivalent resistance (in ohm) of the given network is
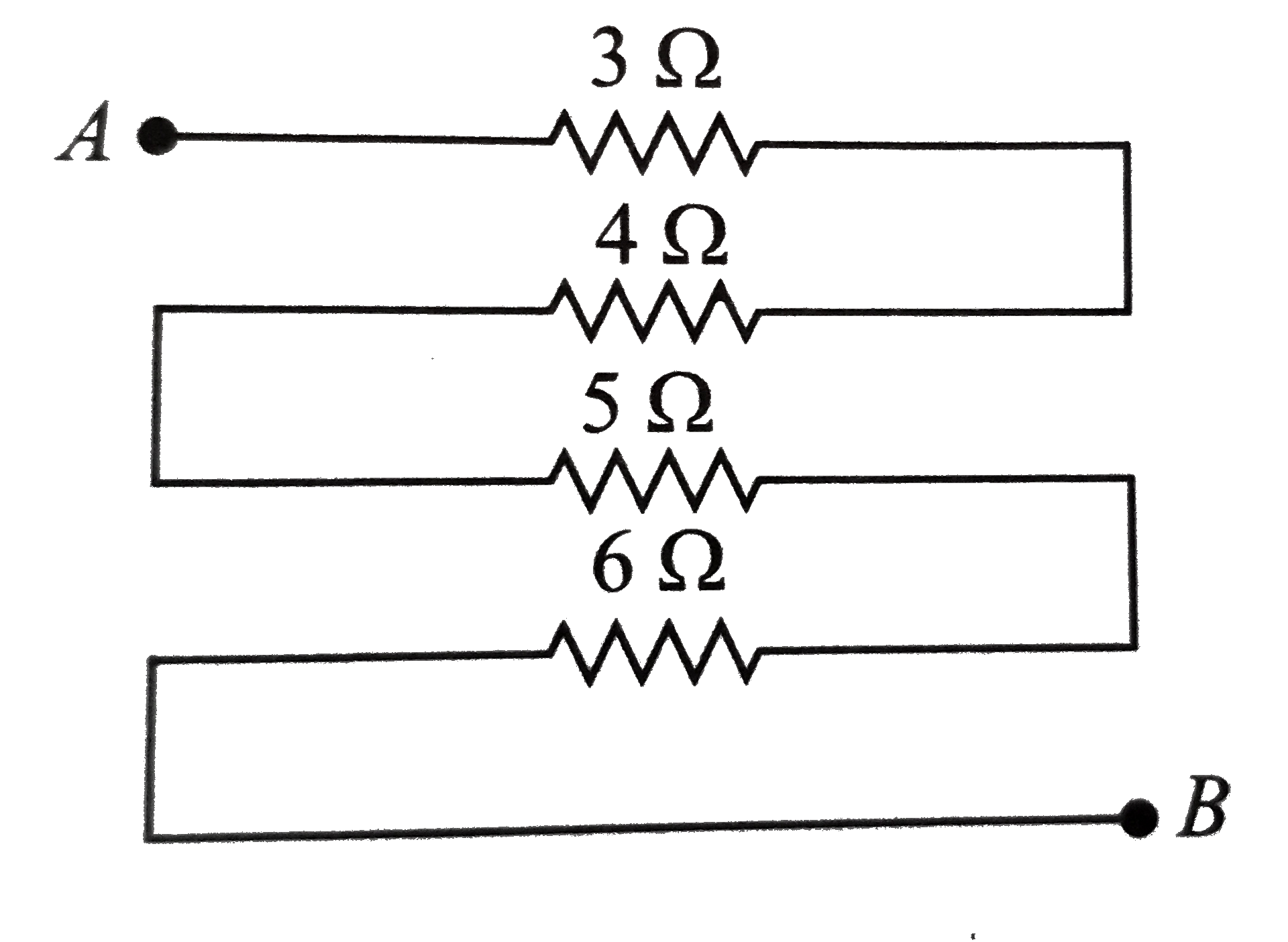 A28B18C26D25
A28B18C26D25
Two resistance wires on joining in parallel the resultant resistance is ohms 65 ohms. One of the wire breaks, the effective resistance is 2 ohms . The resistance of the broken wire is
View SolutionIf all the resistors shown have the value 2 ohm each, the equivalent resistance over AB is

View SolutionA wire has a resistance of 12 ohm . It is bent in the form of equilateral triangle. The effective resistance between any two corners of the triangle is
View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View SolutionTwo resistances are joined in parallel whose resultant is 6/8ohm. One of the resistance wire is broken and the effective resistance becomes 2Ω . Then the resistance in ohm of the wire that got broken was
View SolutionIn the given circuit all resistances are of value R ohm each. The equivalent resistance between A and Bis :
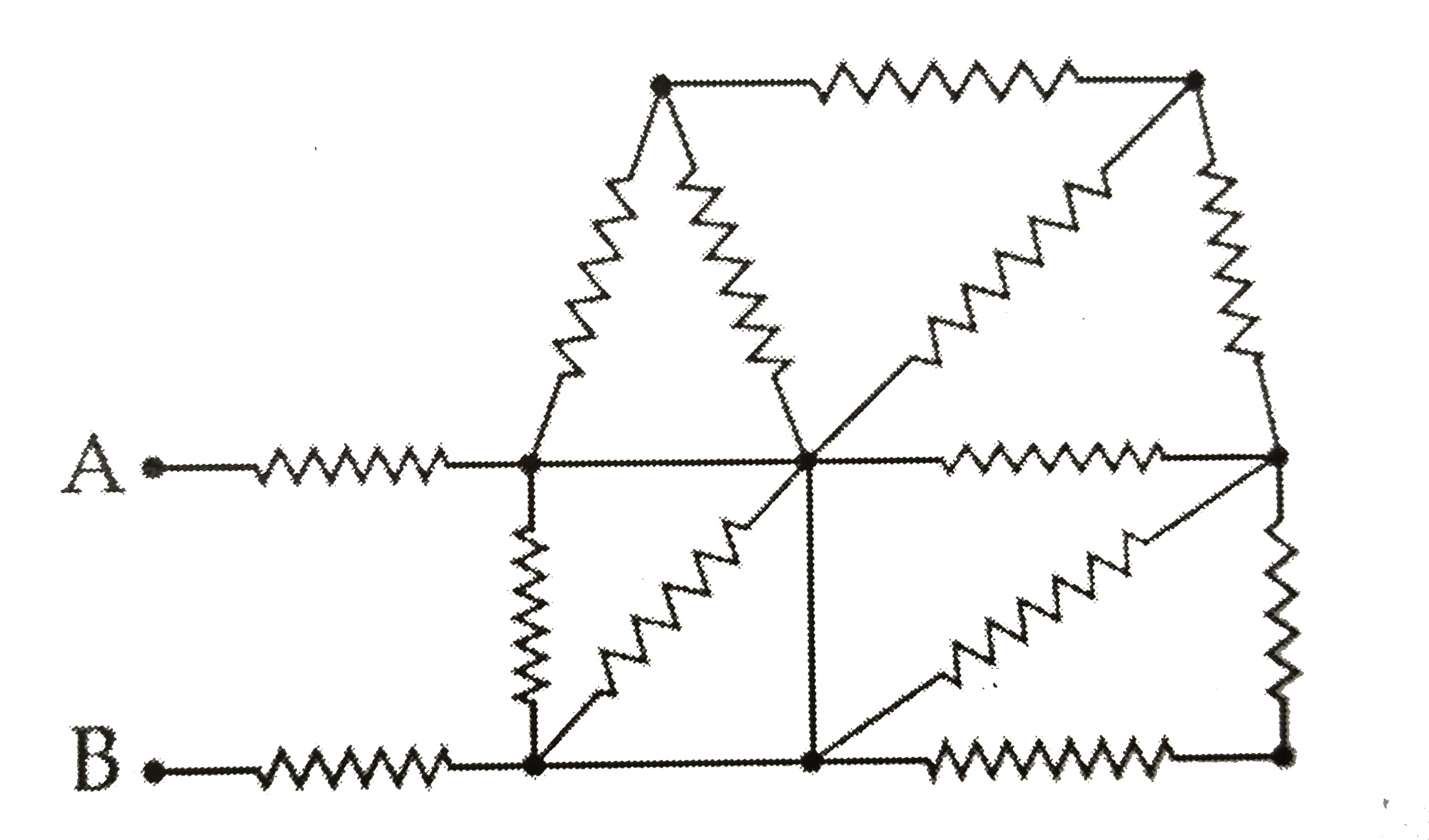
View SolutionThe resultant resistance value of n resistance each of r ohms and connected is series is X. When those n , resistance are connected in parallel , the resultant values is .
View Solution
