By what percentage the impedance in an AC series circuit should be increased so that the power factir changes from (when R is constant)?
200%
100%
60%
40%
The correct Answer is:B
To solve the problem step by step, we need to analyze the power factor changes in an AC series circuit and how it relates to impedance.
Step 1: Understand the Power Factor
The power factor (PF) in an AC circuit is defined as:
PF=cosθ=RZ
where R is the resistance and Z is the impedance.
Step 2: Set Up Initial Conditions
Initially, we have:
PF1=12
This implies:
RZ1=12
From this, we can express the initial impedance Z1:
Z1=2R
Step 3: Set Up Final Conditions
Now, the power factor changes to:
PF2=14
This implies:
RZ2=14
From this, we can express the final impedance Z2:
Z2=4R
Step 4: Calculate the Change in Impedance
Now, we need to find the change in impedance:
ΔZ=Z2−Z1=4R−2R=2R
Step 5: Calculate the Percentage Change in Impedance
The percentage change in impedance is given by:
Percentage Change=ΔZZ1×100=2R2R×100=100%
Final Answer
The impedance should be increased by 100%.
---
The power factor (PF) in an AC circuit is defined as:
PF=cosθ=RZ
where R is the resistance and Z is the impedance.
Initially, we have:
PF1=12
This implies:
RZ1=12
From this, we can express the initial impedance Z1:
Z1=2R
Now, the power factor changes to:
PF2=14
This implies:
RZ2=14
From this, we can express the final impedance Z2:
Z2=4R
Now, we need to find the change in impedance:
ΔZ=Z2−Z1=4R−2R=2R
The percentage change in impedance is given by:
Percentage Change=ΔZZ1×100=2R2R×100=100%
The impedance should be increased by 100%.
Topper's Solved these Questions
Similar Questions
By what percentage the impedance in an AC series circuit should be increased so that the power factor changes from (1/2) to (1/4) (when R is constant)?
View SolutionThe r.m.s current in an AC circuit is 2A. If the wattless current be √3A, what is the power factor?
View SolutionBy what percentage should the pressure of a given mass of a gas be increased so as to decrease its volume by 10% at a constant temperature?
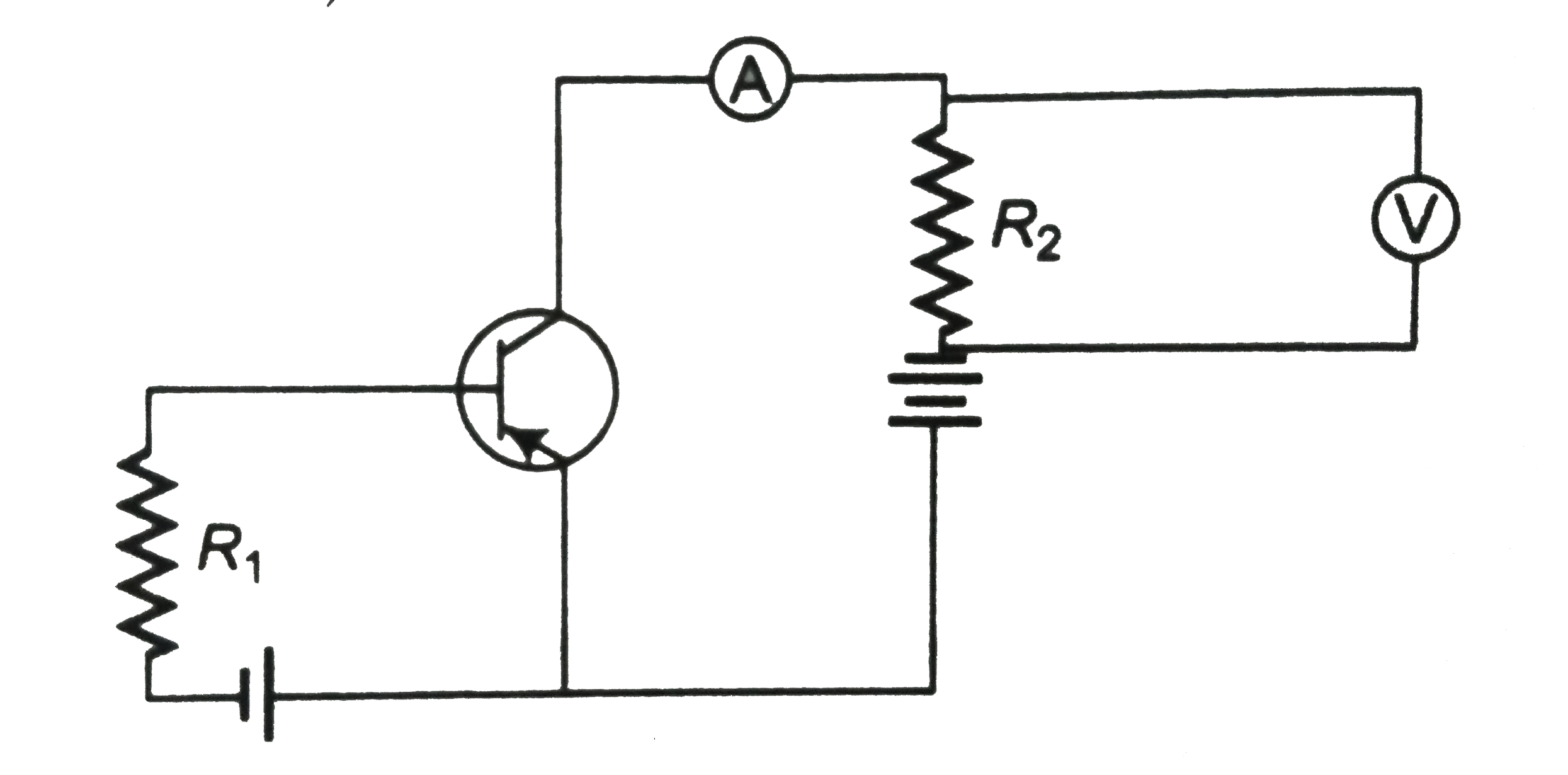
View SolutionIn the given circuit if R1 is increased without disturbing the bias or changing R2 then
View SolutionThe impedance of a series R-C, AC circuit is Z1 for frequency f and Z2 for 2f. If Z1Z2=k, then
View SolutionThe pressure of gas is increased 2 times. What should be the change in its volume so that the temperature and number of moles remains constant ?
View SolutionThe pressure of a gas is increased 2 times. What should be the change in its volume so that the temperature and number of moles remain constant?
View SolutionAssertion (A) If the frequency of the applied AC is doubled , then the power factor of a series R-L circuit decreases.
Reason (R ) Power factor of series R-L circuit is given by cosθ=2R√R2+ω2L2
View SolutionWhen the length of the vibrating segment of a
sonometer wire is increased by 1% the percentage
change in its frequency is
View SolutionIf the power factor in an AC circuit changes from 13 to 19 then by what percent reactance will change (approximately), If resistance remains constant?
View Solution
