In the circuit shown in fig, the time constant of the two braches are equal(=T). Then if the key S is closed at the instant t=0, the time in which the current in the circuit through the battery will rise to its final value of (E/R) will be, (assume that the internal resistance of the battery and of the connecting wire are negligible)
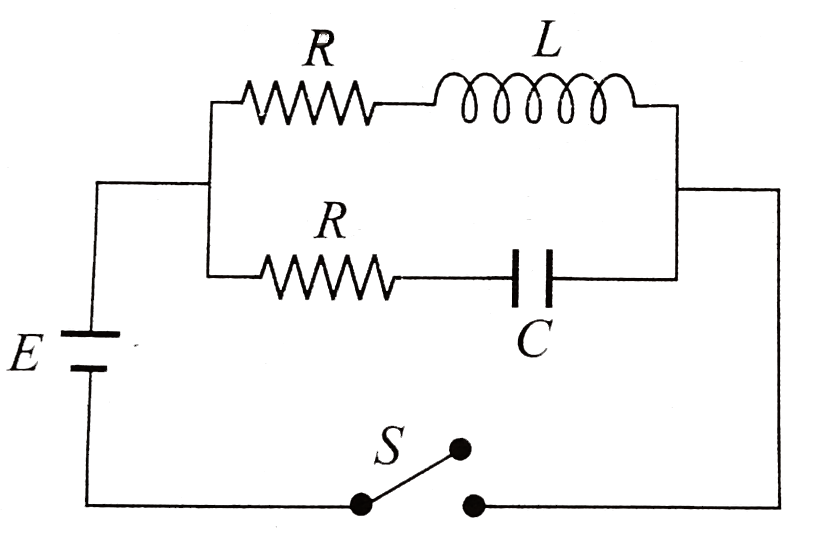
Instantly
t=T2
t=2T
t=∞
The correct Answer is:A
The (L-R) and (C-R) sections having the same time constant are in parallel.
The current through the R-L branch will be unaffacted by the parallel R-C branch
iL(t)=ER[1−r−RtL] ...(i)
Similarly the current in the RC branch is given by
iC(t)=ERe−tRC...(ii)
Hence the current through the battery is
i(t)=iL(t)+iC(t)=ER[1−e−RCt+e−tRC]....(iii)
Time cosntant of RL branch is τL=LR and the time constant of RC branch is τ(C)=RC.
If these are equal , τL=τC=T, equation (iii) becomes
i(t)=ER[1−e−RCt+e−tRC]=ER for all value of tgto=0. Hence the result.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct
34 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension
84 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
Similar Questions
Consider the circuit shown in figure. The current through the battery a long time after the switch S is closed is:

View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
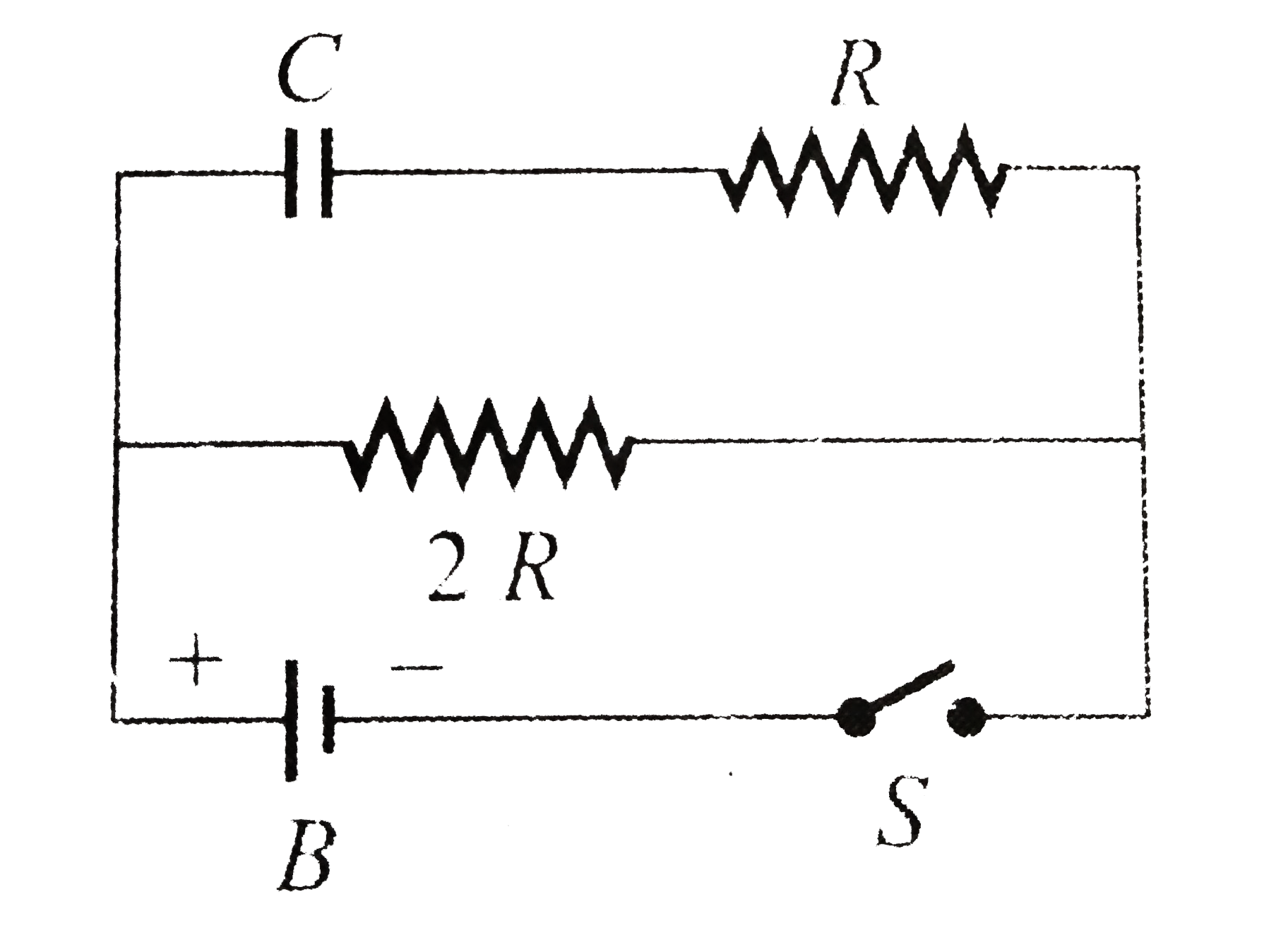
View SolutionIn the circuit shown below, the key K is closed at t = 0. The current through the battery is
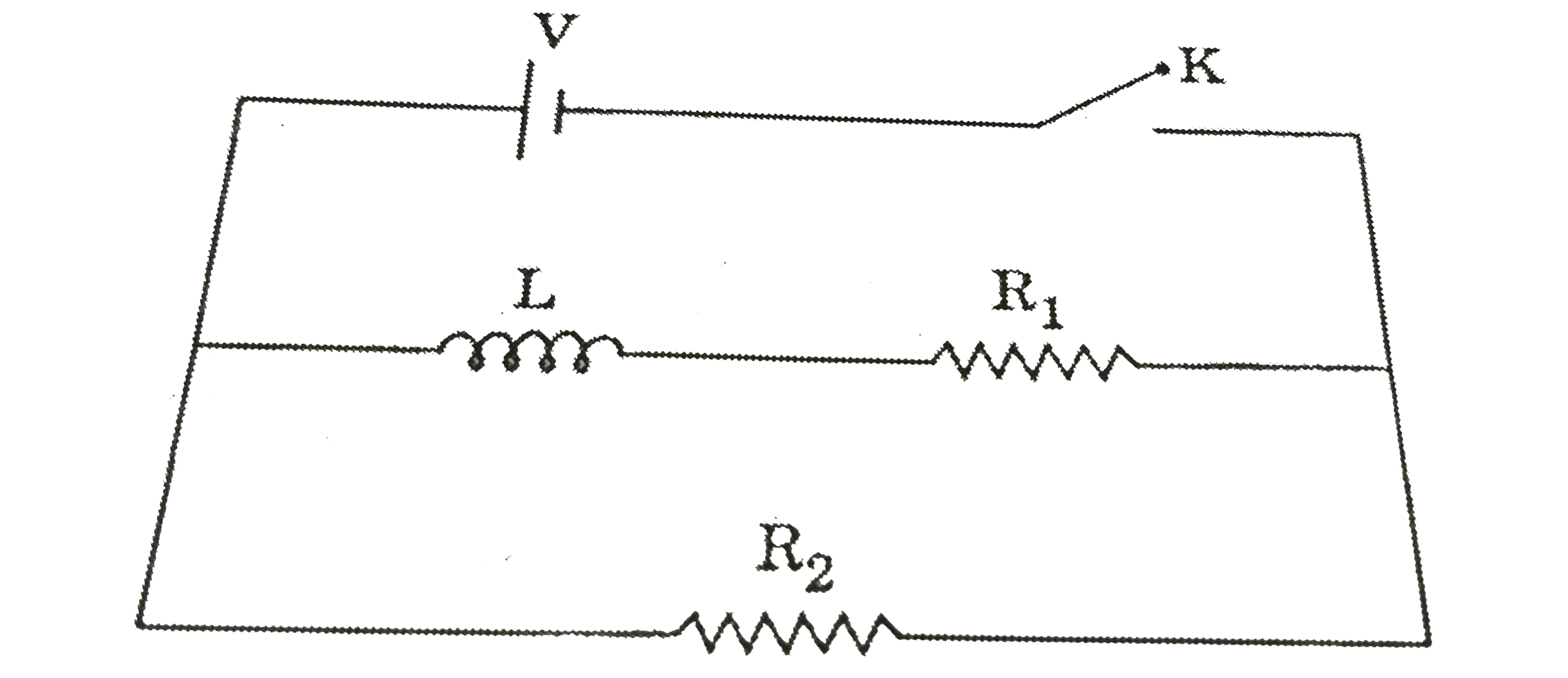
View SolutionIn the circuit shown below, the key K is closed at t =0. The current through the battery is
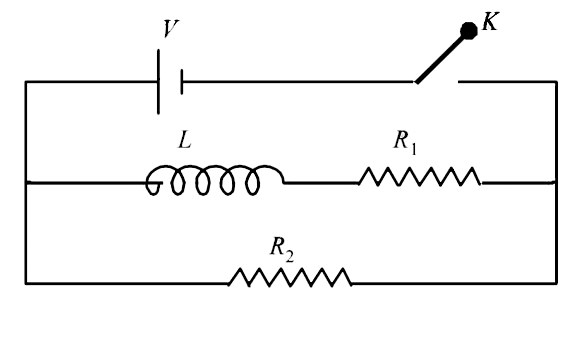
View SolutionIn the circuit shown in figure switch S is closed at time t=0. The charge which passes through the battery in one time constant is

View SolutionIn th circuit the key (K) is closed at t=0. Find the current in ampere through the key (K) at the instant t=102ln2 sec.
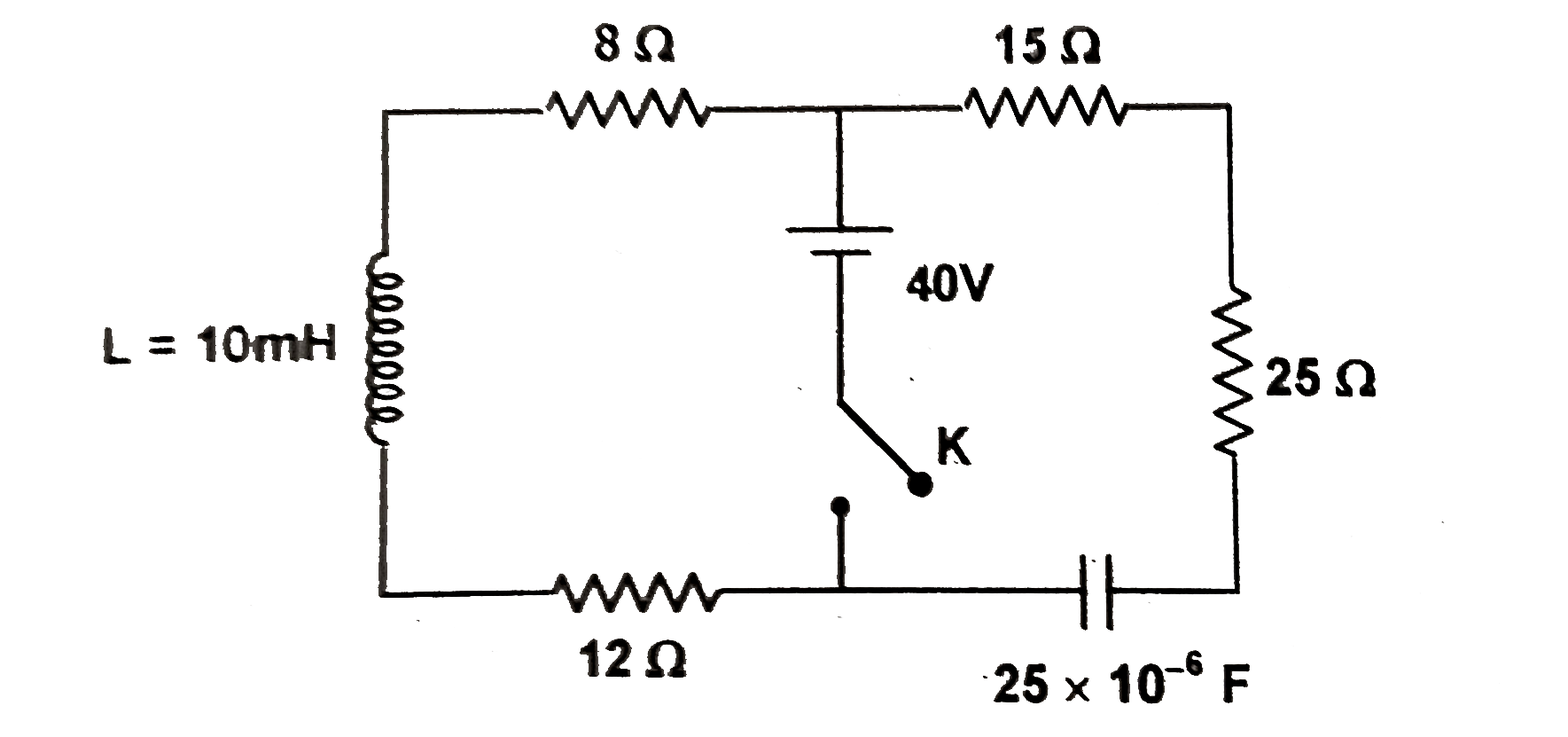
View SolutionIn the circuit shown in figure switch S is closed at time t=0
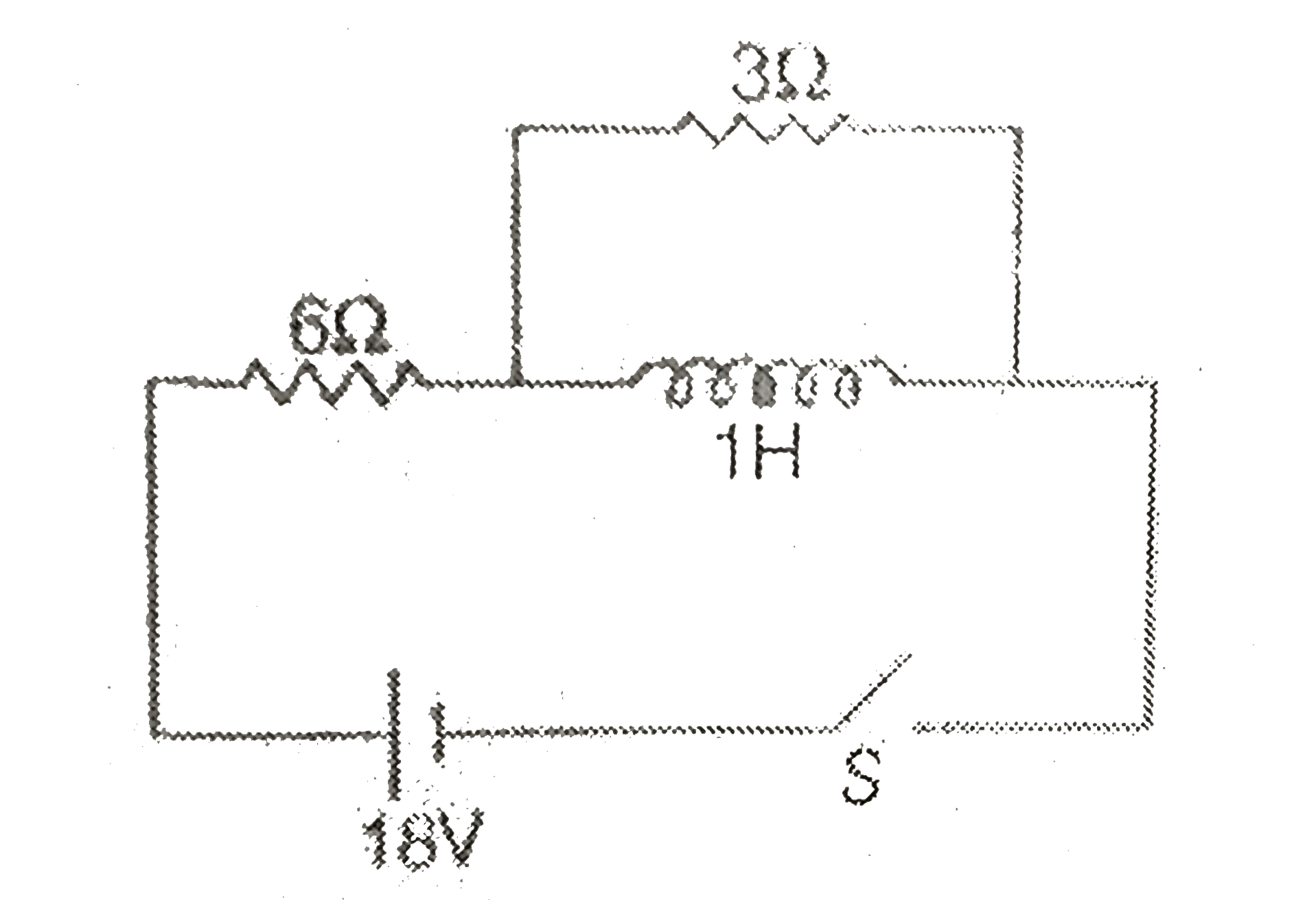
Current I from the battery at time t is given by
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then the current through the battery steady state reached is
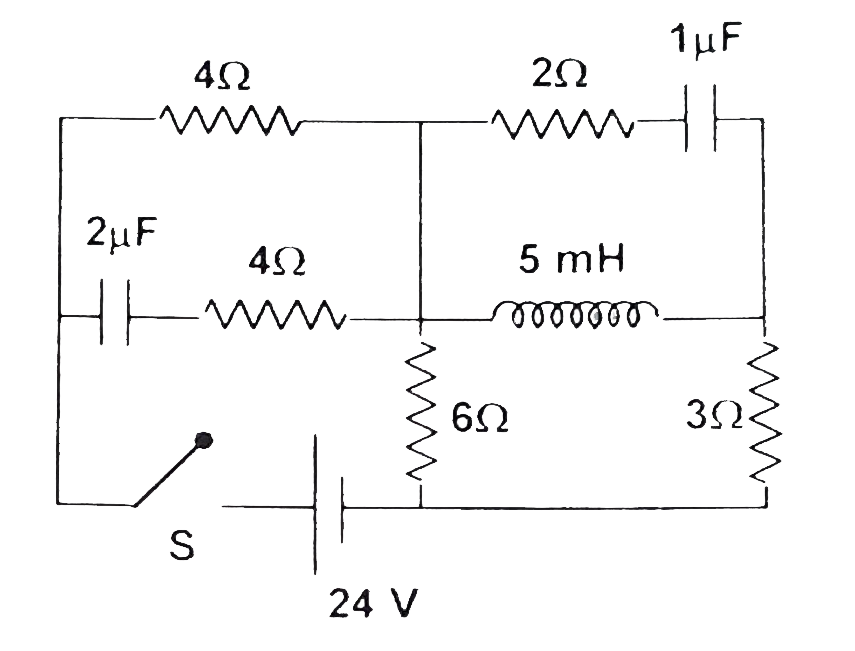
View SolutionIn the circuit shown in figure switch S is closed at time t=0, which statement is true after one time constant of L-R circuit?

View SolutionPassage-III
In the circuit shown, the battery is ideal with emf V. The capacitor is initially uncharged. The switch is closed at time t = 0
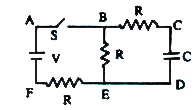
The current in the branch BE at t=∞ is
View Solution
