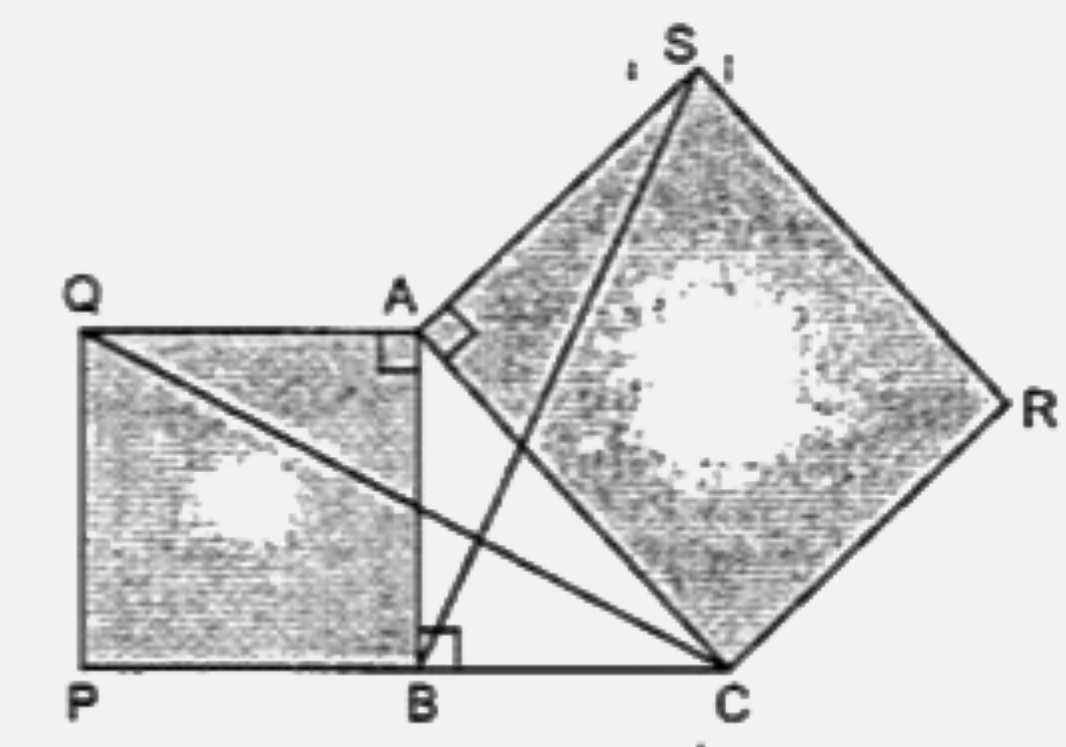
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares.
Prove that :
CQ=BS
The correct Answer is:CQ=BS
Step by step video & image solution for In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that : CQ=BS by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
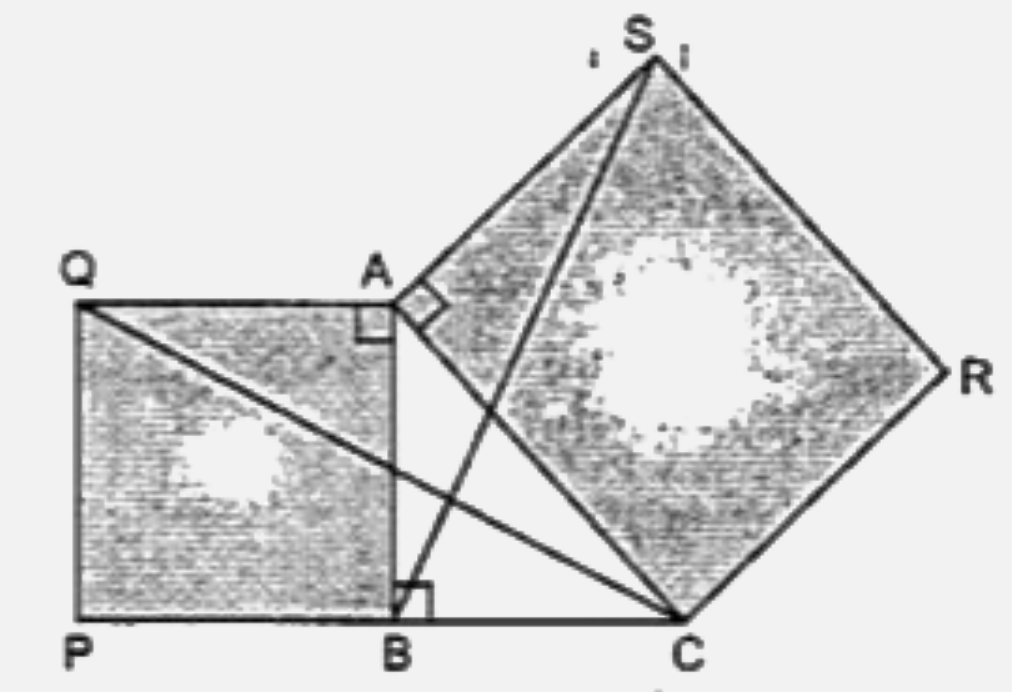
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares.
Prove that :
ΔACQ and ΔASB are congruent
View SolutionIn the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. Prove that :
(i) ΔACQandΔASB are congruent.
(ii) CQ = BS
View Solution
Knowledge Check
In the figure, triangle ABC and ABD are right triangle , what is the value of x?
 A20B30C50D70
A20B30C50D70
In the adjoining figure, ABC is a triangle right-angled at vertex A and AD is altitude.
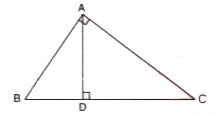
Prove that : ΔABD is similar to ΔCAD.
View SolutionIf triangle ABC is right angled at C, then the value of sec (A+B) is
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
View SolutionIn the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
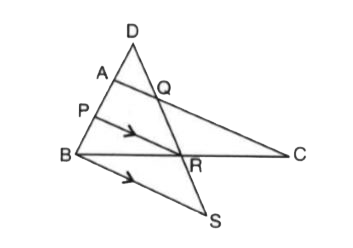
AQ//BS
View SolutionIn the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that:
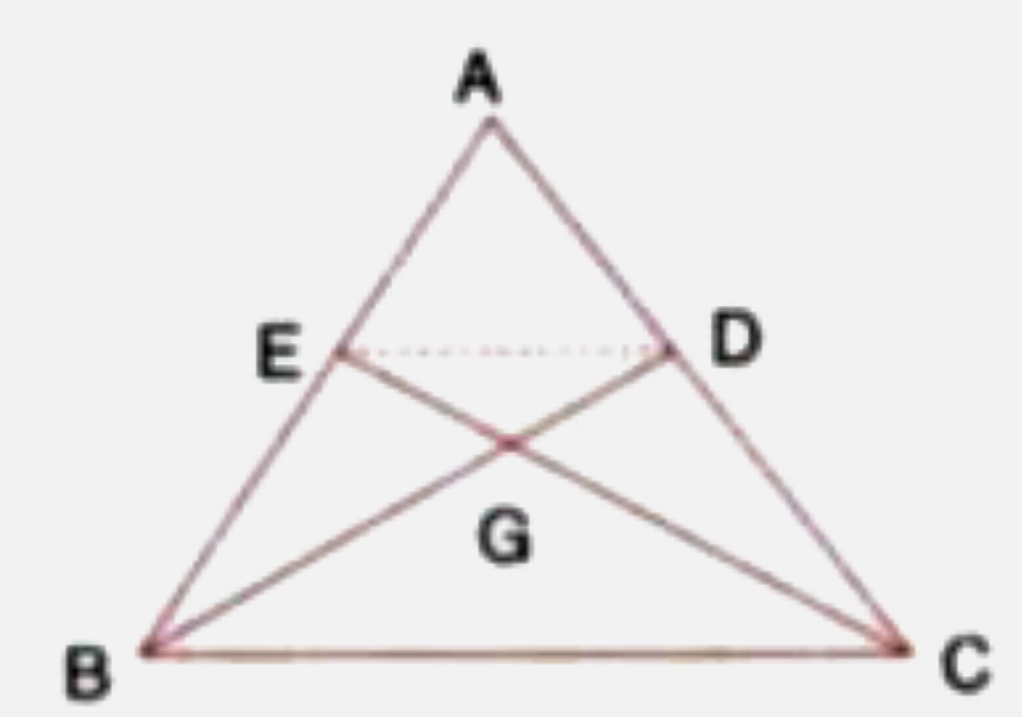
ΔEGD−ΔCGBand (ii) BG=2GD from (i) above.
View SolutionIn a right triangle ABC right-angled at B. if tanA=1, then verify that 2sinAcosA=1.
View SolutionIn the figure, given below, PQR is a right angled triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1:2. Calculate the lengths of PR and QR.

View Solution
