PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
The correct Answer is:MN=LN
Step by step video, text & image solution for PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
ABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
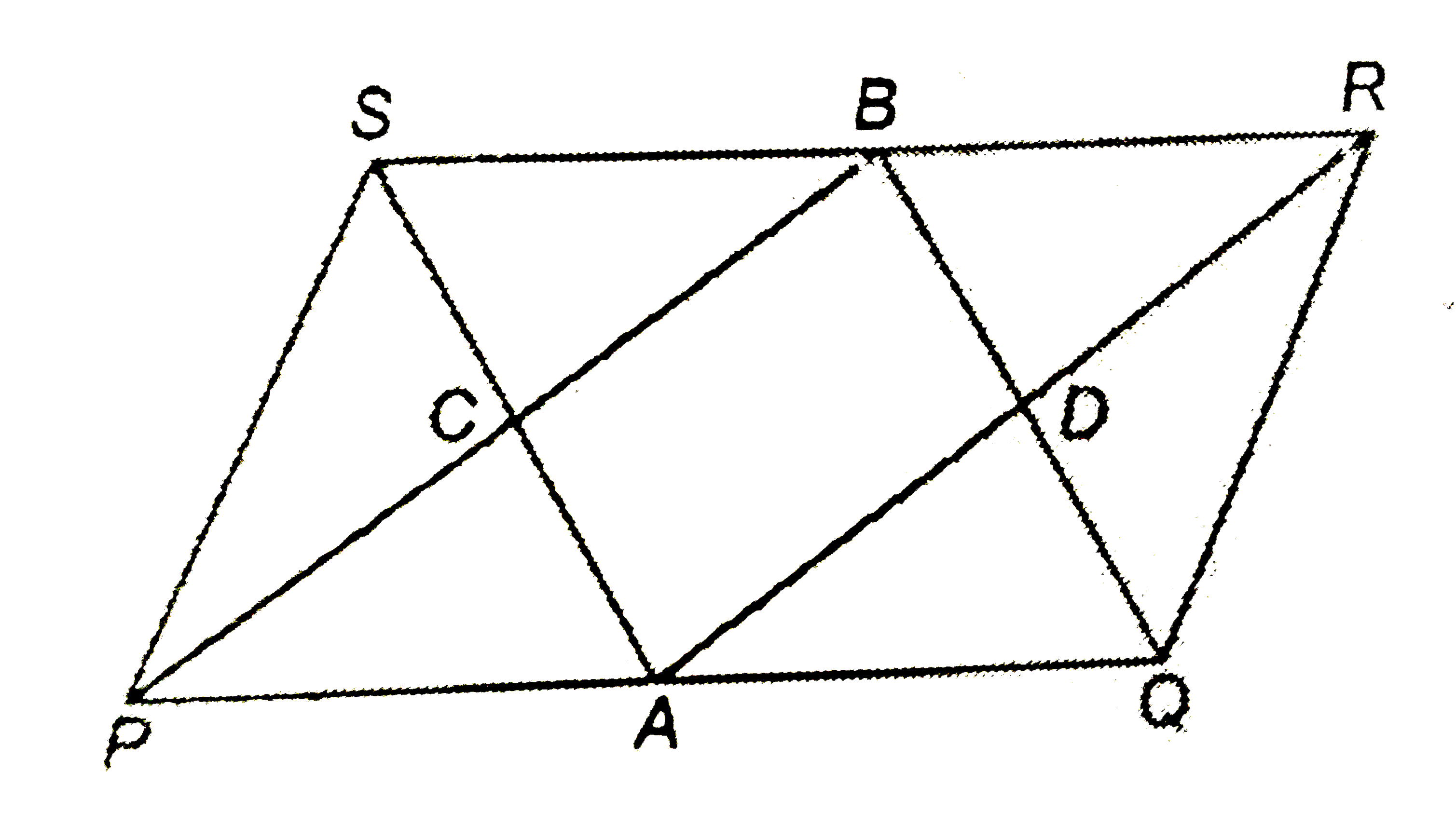
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
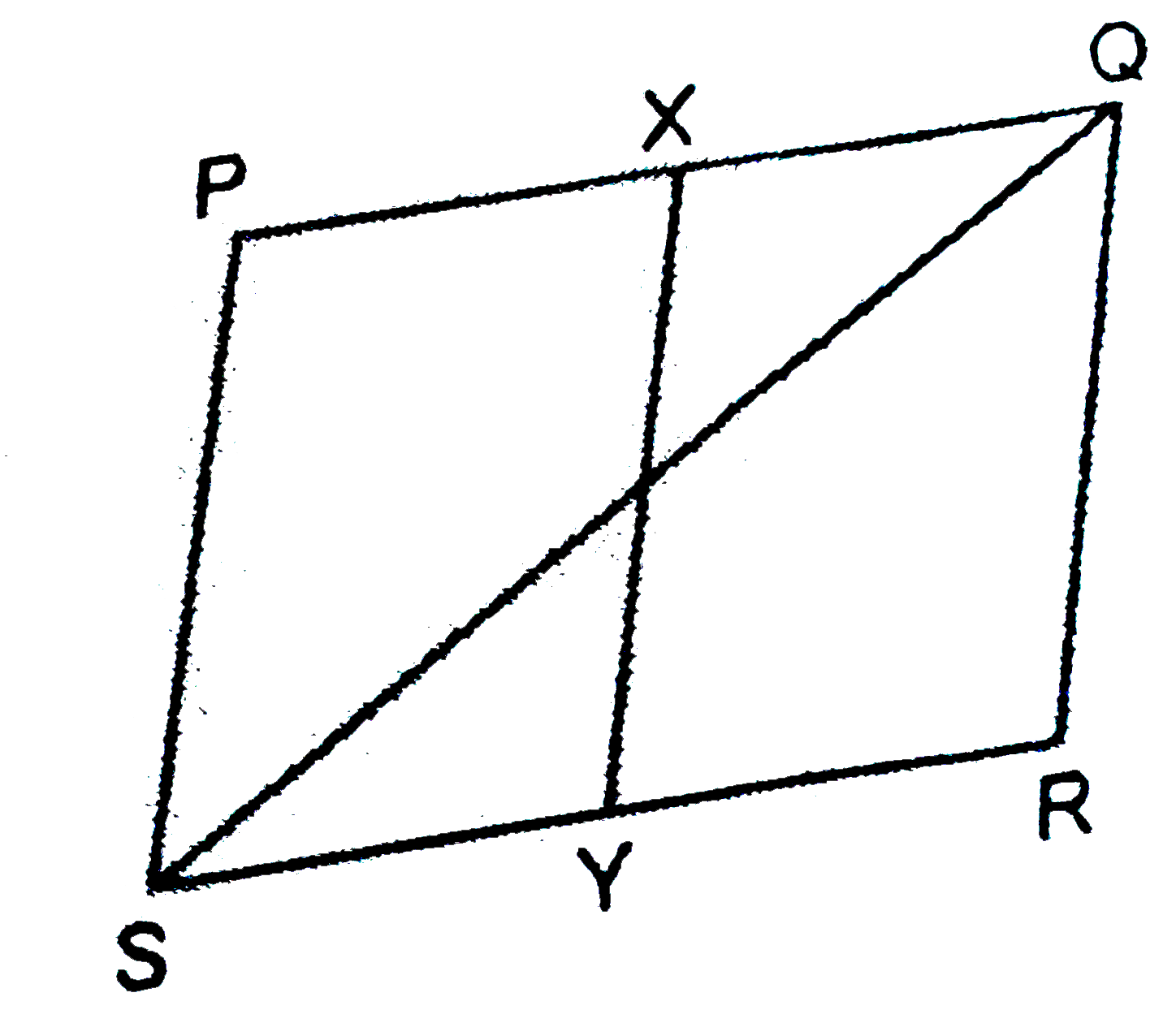
View SolutionIn ΔABC,AB=AC.D,Eand F are mid-points of the sides BC, CA and AB respectively . Show that :
AD and FE bisect each other.
View SolutionIn ΔABC,D,E and F are mid-point of sides AB ,BC and AC respectively , Prove that AE and DF bisect each other.
View SolutionPQRS is a parallelogram. RA and RB are perpendiculars from R on PQ and PS, respectively. If RA = 15 cm, RB = 22 cm, and QR = 26 cm, find PQ.
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram. Figure
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid-points of sides AB and DC respectively. Show that AXCY is a parallelogram.
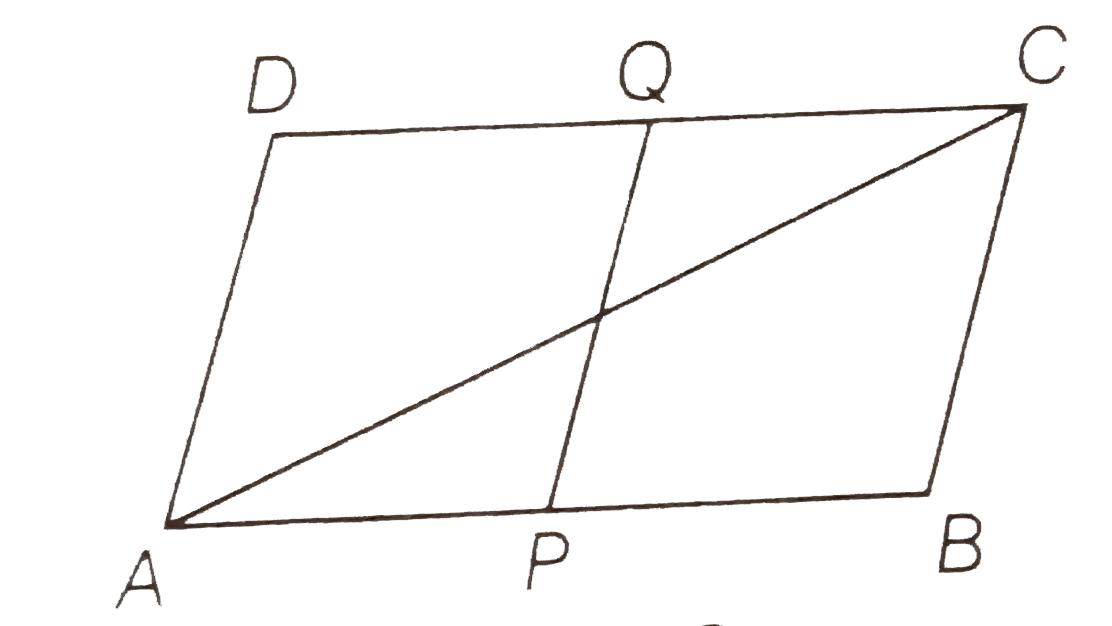
View SolutionPoints P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP=CQ. Show that AC and PQ bisect each other.
View Solution