A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will be
S2,S4,andS5
S1,S3,S4,andS6
S1,S2,andS3
S2,S3,andS4
The correct Answer is:B
For S1,→A=L2(−ˆj),→E=−5xˆi+3zˆk.
Here →E⊥→A , so ϕs1=0.
For S2,→A=L2ˆk,→E=−5xˆi+3Lˆk.
Here −5xˆi is perpendicular to →A , so no flux due to this component.
ϕs2=(3Lˆk).L2ˆk=3L3=81×10−3Nm2C−1
For S3,→A=L2ˆj,→E=−5xˆi+3zˆk.
Here →E⊥→A , so ϕs3=0.
For S4,→A=−L2ˆk,→E=−5xˆi+0ˆk ("since" z = 0).<br>Herevec _|_ vec(A),sophi_(S_(4)) = 0.<br>ForS_(5) , vec(A) = L^(2) hat (i) , vec (E ) = - 5 L hat(i) + 3z hat(k).<br>Nofluxdue→3 z hat (k) compo≠nt.<br>phi_(S_(5)) = ( - 5 L hat (i)) . L^(2) hat(i) = - 5 L^(3) = - 135 xx 10^(-3) Nm^(2) C^(-1)<br>For S_(6), vec(A) = - L^(2) hat(i) , vec( E) = 0 hat (i) + 3 z hat(k)(sincex = 0).<br>Herevec(E ) _|_ vec(A),sophi_(s_(6)) = 0.<br>Totalfluxthroughthecubeisphi = phi (S_(1) + S_(2) + S_(3) + S_(5) + S_(6))<br>= 81 xx 10^(-3) - 135 xx 10^(-3) = - 54 xx 10^(-3) Nm^(2) C^(-1)<br>Now,phi = ( q_(in))/( epsilon_(0)) or q_(in) = phi epsilon_(0) = - 0.054 epsilon_(0) C
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type
7 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct
8 Videos
- ELECTRIC CURRENT AND CIRCUITBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger
8 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
Similar Questions
A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total electric charge inside the cube is
View SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube is
View SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
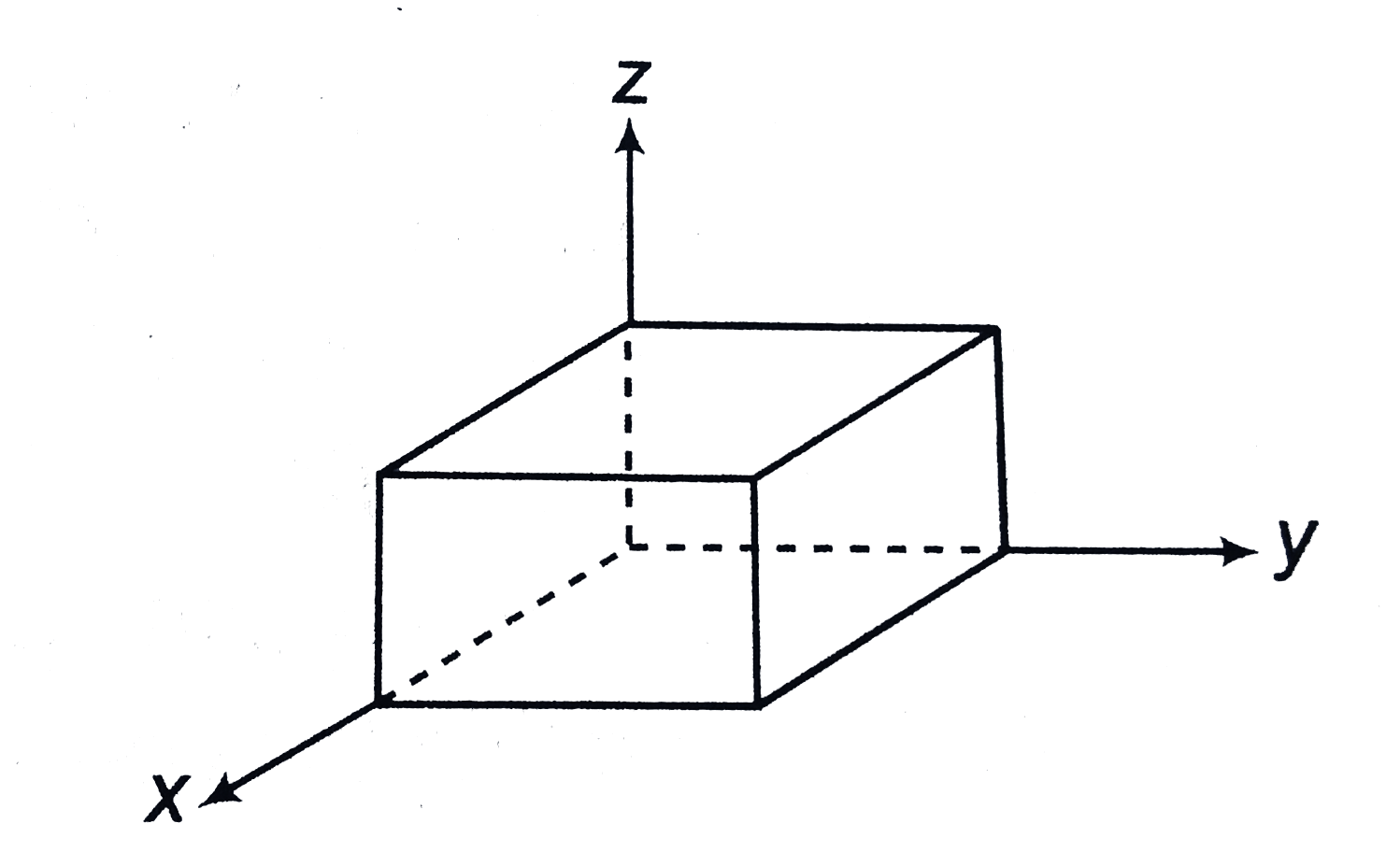
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
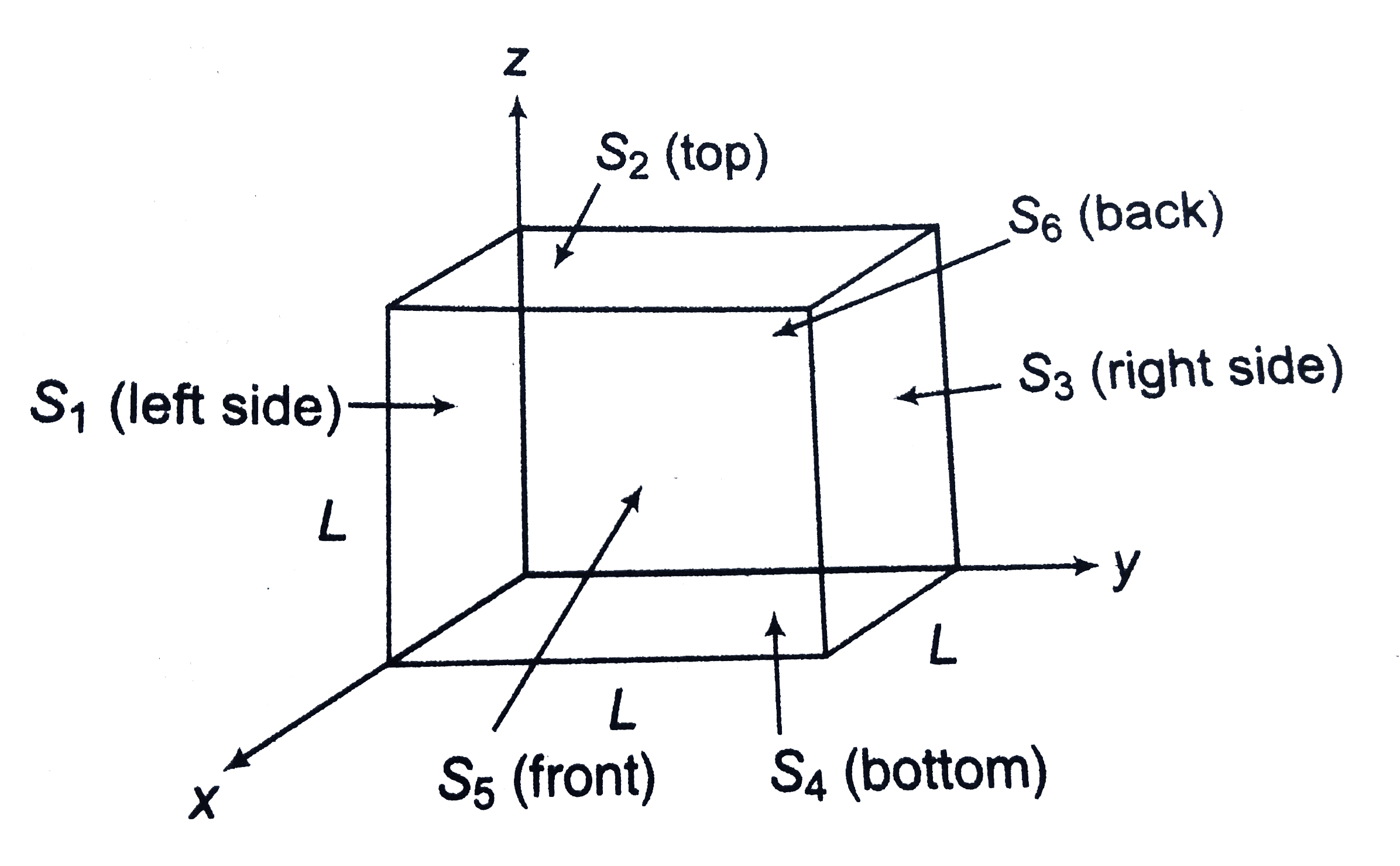
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.
View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionA bollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
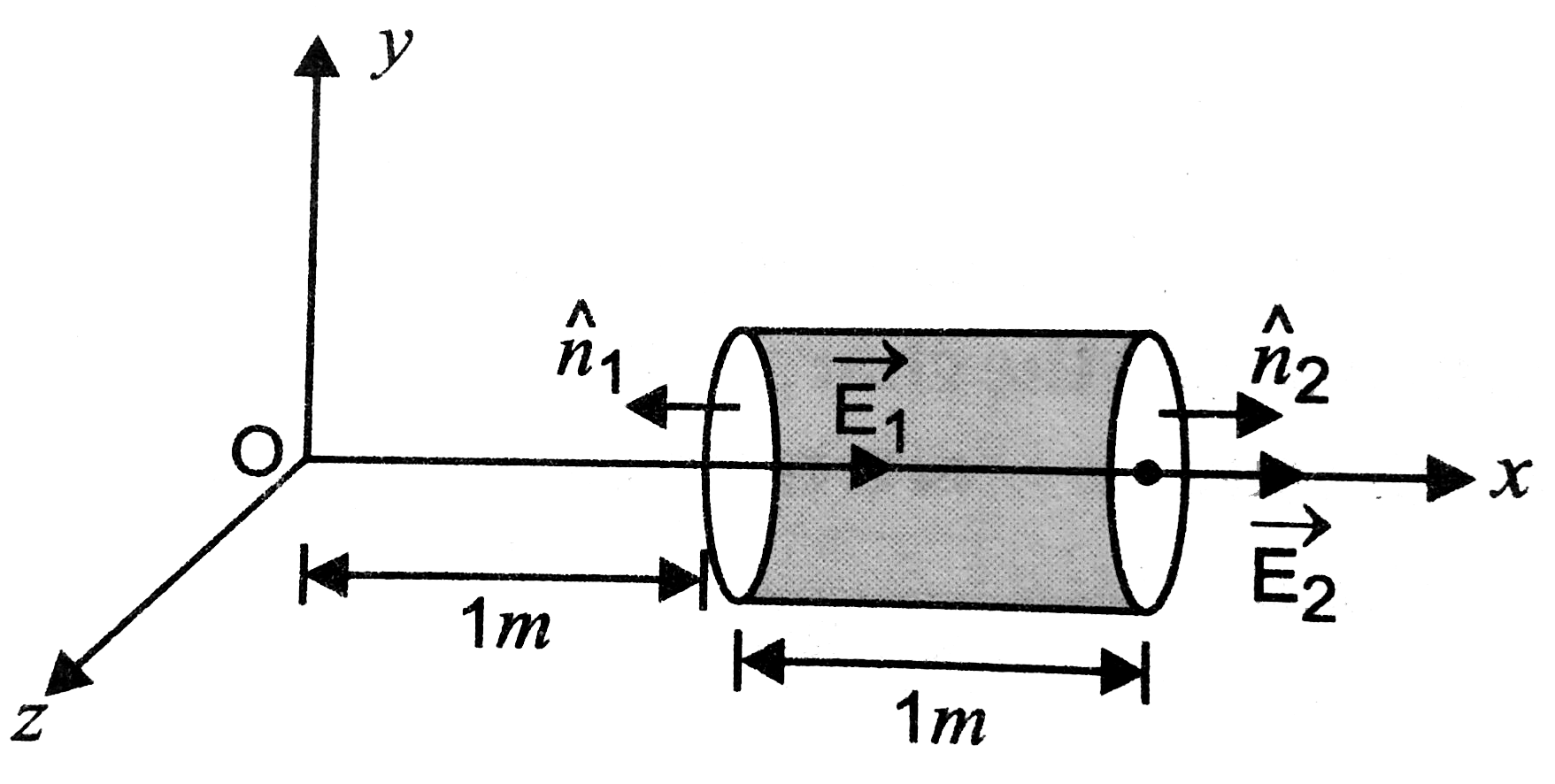
View SolutionA hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.
View SolutionA cube of edge length l=2.50cm is positioned as shown in Fig. 3.20. A uniform magnetic field given by →B=(5.00ˆi+4.00ˆj+3.00ˆk)T exists throughout the region.
(a) Calculate the flux through the shaded face.
(b) What is the total flux through the six faces ?

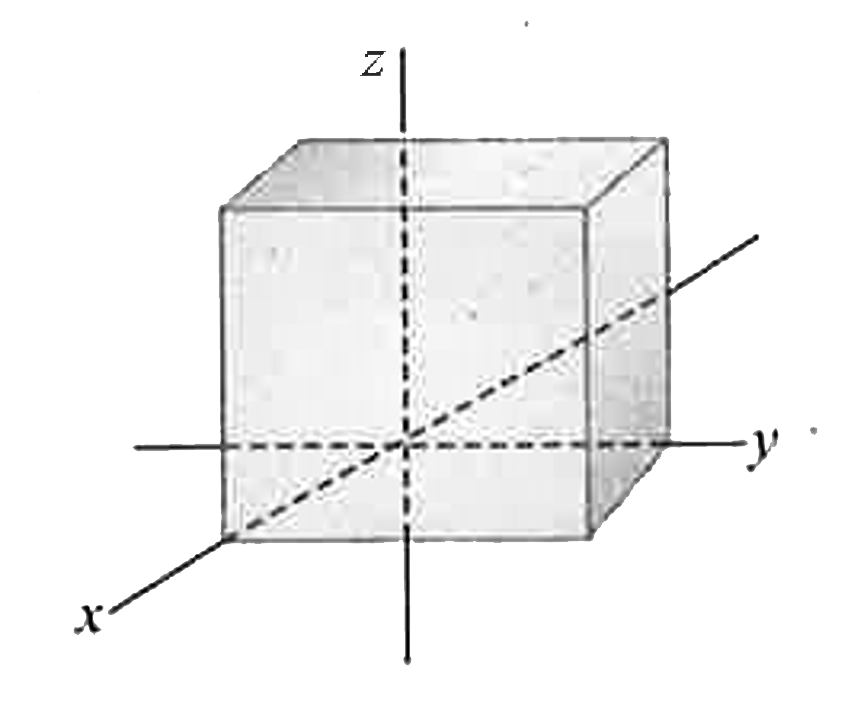
View SolutionThe cube in figure has edge length √2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00ˆi,(b)−2.00ˆj,and(c)−3.00ˆj+4.00ˆk . (d) what is the total flux through the cube for each field ?
View SolutionA surface element →ds=5ˆi is placed in an electric field →E=4ˆi+4ˆj+4ˆk. What is the electric flux emanting from the surface ?
View Solution
