A conical pendulum consists of a mass M suspended from a string of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rhe and has velocity wˆ.At time t, the angular momentum vector of the mass M about the point from which the string suspended is :
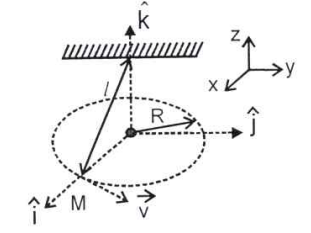
MvRˆk
Mh––ak
(Mv)/[√l2−R2lˆi+Rlˆk]
(−Mv)/[√l2−R2lˆi+Rlˆk]
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
A conical pendulum consists of a mass M suspended from a strong sling of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and vˆj velocity. At time t the angular momentum vector of mass M about the point from which the string passes on the ceiling is
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View Solution
Knowledge Check
A conical pendulum consists of a mass M suspended from a string of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and has velocity vˆj. At time t, the angular momentum vector of the mass M about the point from which the string suspended is
 AMυRˆkBmυlˆkCMυl[(√l2−R2lˆi)+Rlˆk]D−Mυl[(√l2−R2lˆi)+Rlˆk]
AMυRˆkBmυlˆkCMυl[(√l2−R2lˆi)+Rlˆk]D−Mυl[(√l2−R2lˆi)+Rlˆk]A conical pendulum consists of a mass M suspended from a strong sling of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and vˆj velocity. At time t the angular momentum vector of mass M about the point from which the string passes on the ceiling is
 AMvRˆkBMvlˆkCMvl[√l2−R2lˆi+Rlˆk]D−Mvl[√l2−R2lˆi+Rlˆk]
AMvRˆkBMvlˆkCMvl[√l2−R2lˆi+Rlˆk]D−Mvl[√l2−R2lˆi+Rlˆk]A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12
A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find a. the speed of the particle and b. the tension in the string. Such a system is called a conical pendulum.
View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
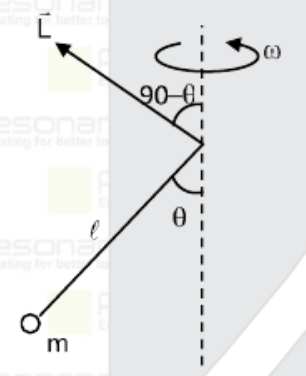
View SolutionA particle of mass m is suspended from point O and undergoes circular motion in horizontal plane as conical pendulum as shown in figure.

View Solution
