A ring made of insulating material is rolling without slipping on a horizontal surface with velocity of centre of mass V0. A conducting wire of length 2R (R = radius of ring) is fixed between two points of the circumference. At an instant, the wire is in vertical position as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the ring. The magnitude to emf induced between the ends of wire is
2BV0R
BV0R
3BV0R
4BV0R
The correct Answer is:A
To solve the problem, we need to determine the induced electromotive force (emf) in the conducting wire fixed on the circumference of the rolling ring. We will use the formula for induced emf in a conductor moving through a magnetic field.
1. Identify the parameters:
- Let the radius of the ring be R.
- The length of the conducting wire is 2R.
- The velocity of the center of mass of the ring is V0.
- The magnetic field B is uniform and perpendicular to the plane of the ring.
2. Understand the motion:
- The ring is rolling without slipping. This means that the point of contact with the ground is momentarily at rest while the center of mass moves with velocity V0.
3. Use the formula for induced emf:
- The induced emf (E) in a wire moving through a magnetic field is given by:
E=V⋅B⋅L
- Where:
- V is the velocity of the wire (which is the same as the velocity of the center of mass, V0).
- B is the magnetic field strength.
- L is the length of the wire.
4. Substitute the known values:
- Here, L=2R (the length of the conducting wire).
- Therefore, substituting the values into the formula:
E=V0⋅B⋅(2R)
5. Simplify the expression:
- This simplifies to:
E=2V0BR
6. Conclusion:
- The magnitude of the induced emf between the ends of the wire is:
E=2V0BR
Final Answer:
The magnitude of the emf induced between the ends of the wire is 2V0BR.
---
- Let the radius of the ring be R.
- The length of the conducting wire is 2R.
- The velocity of the center of mass of the ring is V0.
- The magnetic field B is uniform and perpendicular to the plane of the ring.
- The ring is rolling without slipping. This means that the point of contact with the ground is momentarily at rest while the center of mass moves with velocity V0.
- The induced emf (E) in a wire moving through a magnetic field is given by:
E=V⋅B⋅L
- Where:
- V is the velocity of the wire (which is the same as the velocity of the center of mass, V0).
- B is the magnetic field strength.
- L is the length of the wire.
- Here, L=2R (the length of the conducting wire).
- Therefore, substituting the values into the formula:
E=V0⋅B⋅(2R)
- This simplifies to:
E=2V0BR
- The magnitude of the induced emf between the ends of the wire is:
E=2V0BR
The magnitude of the emf induced between the ends of the wire is 2V0BR.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions

A wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View Solution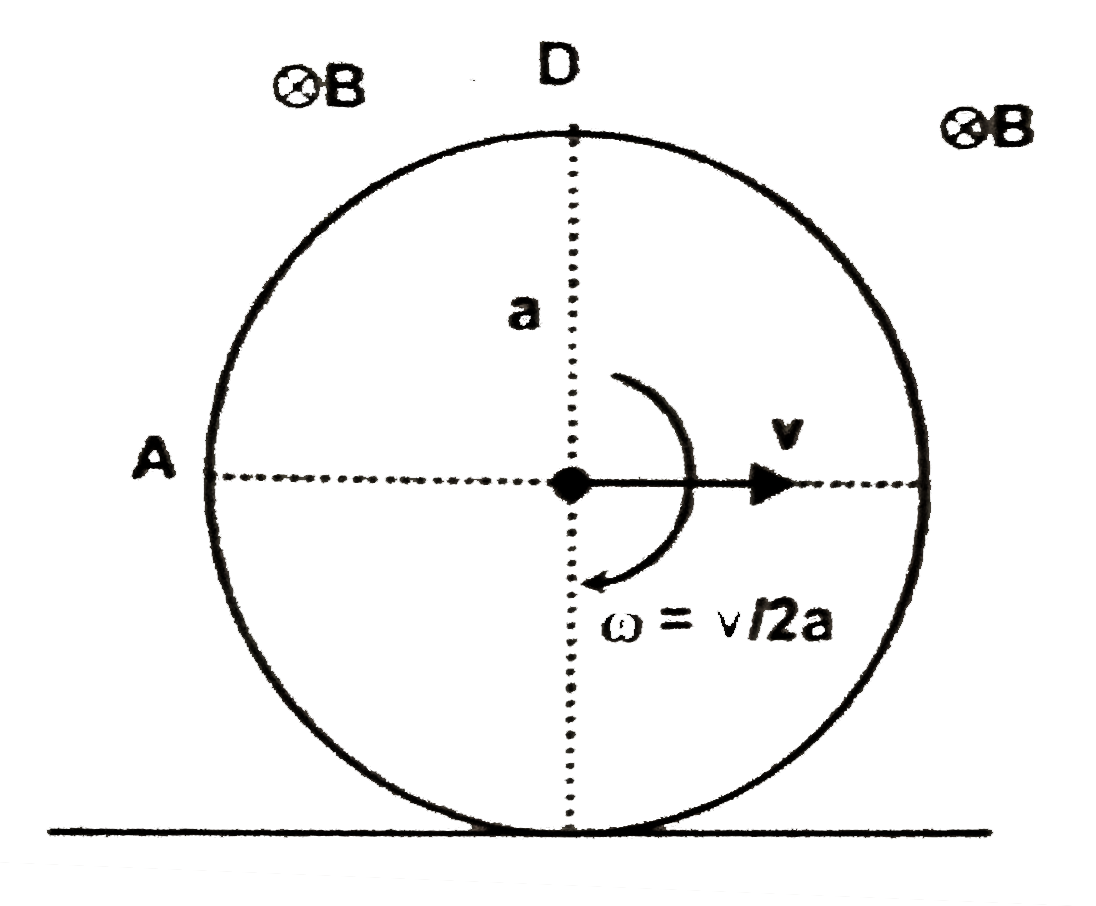
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
A uniform thin ring of mass 0.4kg rolls without slipping on a horizontal surface with a linear velocity of 10 cm/s. The kinetic energy of the ring is
View SolutionTwo conducting rings P and Q of radius r and 3r move in opposite directions with velocities 2v and v respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings a
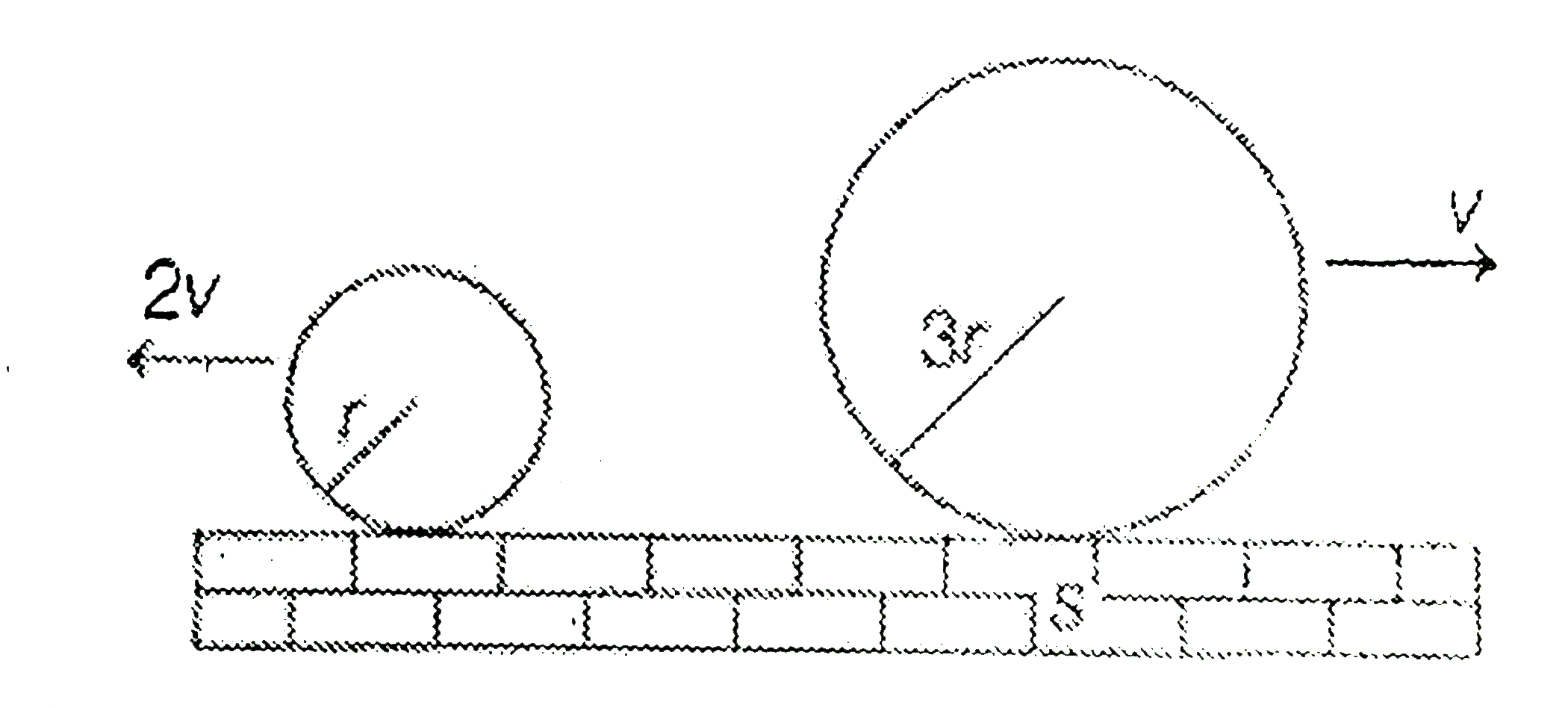
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
View SolutionA ring rolls without slipping on a horizontal surface. At any instant its position is as shown in the figure.
View SolutionA conducting straight wire PQ of length l is fixed along as diameter of a non conducting ring as shown in the figure. The ring is given a pure rolling motion as shown. Field B is horizontal in direction and perpendicular to the plane of ring. The magnitude of induced EMF in the wire PQ at the position shown in figure will be

View SolutionA conducnting straight wire PQ of length l is fixed along as diameter of a non conducting ring as shown in the figure. The ring is given a pure rolling motion on as horizontal masgnetic field B in horizontal direction perpendicular to the plane of ring. The magnitude of induced emf in the wire PQ at the position shown in figure will be

View SolutionTwo conducting rings of radii r and 2r move in apposite directions with velocities 2υ and υ respectively on a conducting surface S. There is a uniform magnetic field of magnitude B perpendicular to the plane of the rings. The potential difference between the highest points of the two rings is
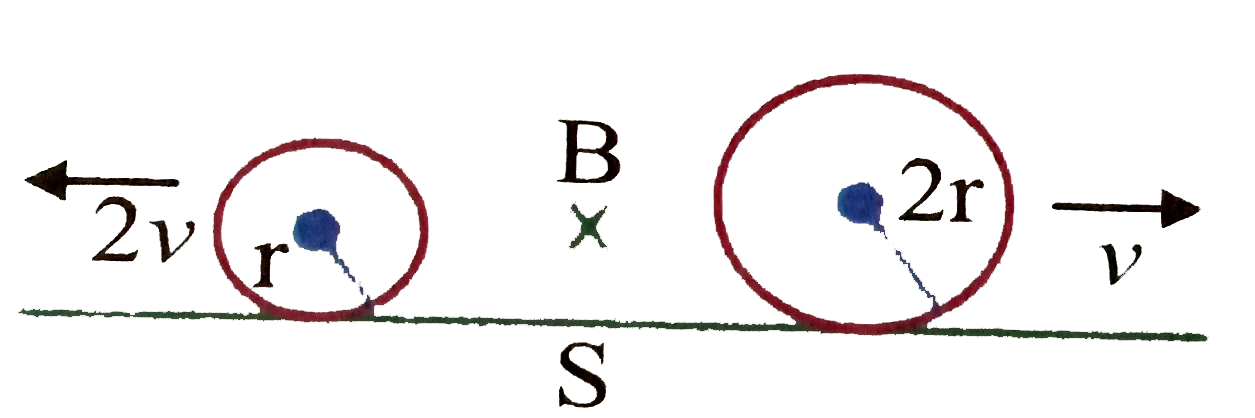
View Solution

