A capacitor in LC oscillatory circuit has a maximum potential of V volts and maximum energy E. When the capacitor has a potential V1 volts and energy E1 joules, what is the emf across the inductor and energy stered in the magnetic field
V−V1,E−E1
V−V1,E1
V1,E1
V1,E−E1
The correct Answer is:D
To solve the problem, we need to analyze the LC oscillatory circuit and apply the principles of energy conservation and the relationships between voltage, energy, and capacitance.
1. Understanding the LC Circuit:
- In an LC circuit, energy oscillates between the capacitor and the inductor. The maximum energy stored in the capacitor when it is fully charged is given by E=12CV2, where V is the maximum voltage across the capacitor.
2. Energy Stored in the Capacitor:
- When the capacitor has a voltage V1, the energy stored in the capacitor at this moment is given by:
E1=12CV21
3. Total Energy Conservation:
- The total energy E in the LC circuit is conserved. Therefore, the total energy can be expressed as:
E=E1+EL
where EL is the energy stored in the inductor.
4. Finding the Energy in the Inductor:
- Rearranging the energy conservation equation gives us:
EL=E−E1
5. Finding the EMF across the Inductor:
- The potential difference (emf) across the inductor VL is equal to the voltage across the capacitor at that moment, which is:
VL=V1
Final Answers:
- The emf across the inductor is V1.
- The energy stored in the magnetic field of the inductor is E−E1.
- In an LC circuit, energy oscillates between the capacitor and the inductor. The maximum energy stored in the capacitor when it is fully charged is given by E=12CV2, where V is the maximum voltage across the capacitor.
- When the capacitor has a voltage V1, the energy stored in the capacitor at this moment is given by:
E1=12CV21
- The total energy E in the LC circuit is conserved. Therefore, the total energy can be expressed as:
E=E1+EL
where EL is the energy stored in the inductor.
- Rearranging the energy conservation equation gives us:
EL=E−E1
- The potential difference (emf) across the inductor VL is equal to the voltage across the capacitor at that moment, which is:
VL=V1
- The emf across the inductor is V1.
- The energy stored in the magnetic field of the inductor is E−E1.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A capacitor in an LC oscillation has a maximum potential difference of 1.5 and a maximum energy 360μJ. At a certain instant the energy in the capacitor is 40μJ, the potential difference across the capacitor is V volt?
View SolutionAn LR series circuit has L=1H and R=1Ω.It is connected across an emf of 2V.The maximum rate at which energy is stored in the magnetic field is:

View SolutionThe energy stored in a capacitor of capacity C and potential V is given by
View SolutionIn oscillating Lc circuit, the total stored energy is U and maximum charge upon capacitor is Q2, the energy stored in the inductor is
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4x10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionA parallel plate capacitor is charged to a potential difference of 50 volts. It is then discharged through a resistance for 2 seconds and its potential drops by 10 volts. Calculate the fraction of energy stored in the capacitance.
View SolutionA circuit has section AB as shown in The emf of the cell is 10V, and the capacitors have capacitances C1=1μF and C2=2μF. Find the voltage across each capacitor.
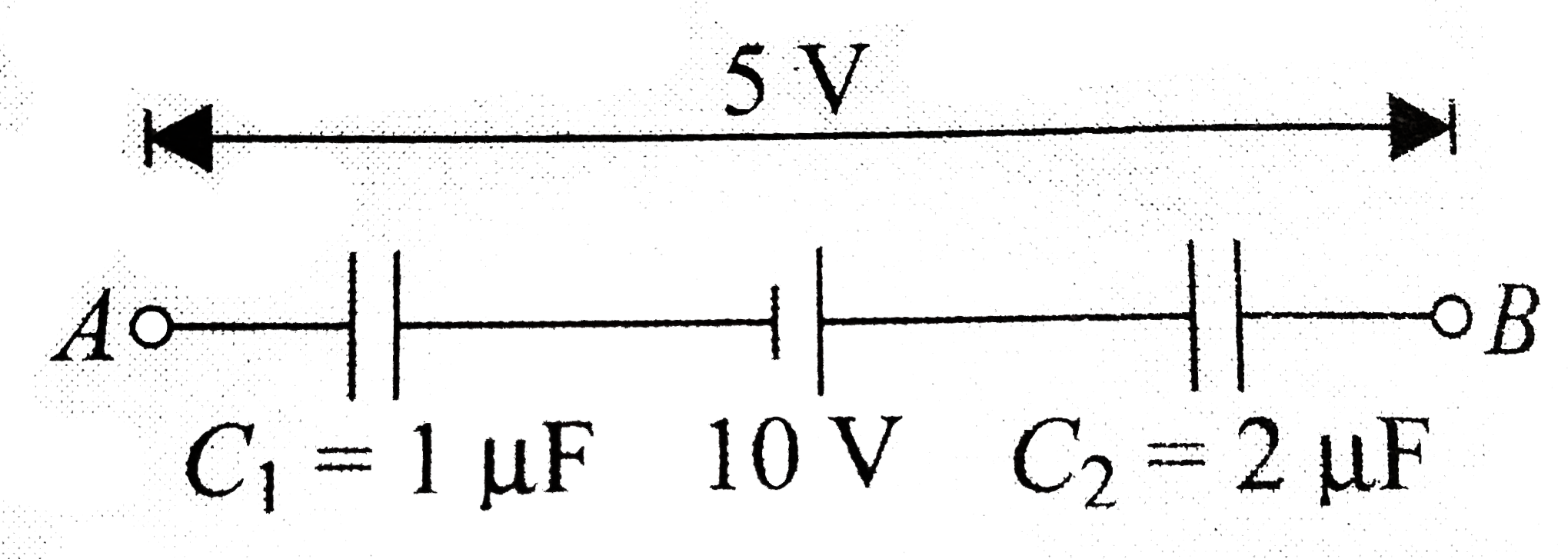 .
.
View SolutionA capacitor when charged by a potential difference of 200 Volts, stores a charge of 0.1C. By discharging energy liberated by the capacitor is-
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View Solution
