In an electric iron heat producedm is same, whether it is connected across an A.c. source or across 50 V constant voltage. R.M.S. value of the A.C. voltage applied is
50 V
Zero
50√2V
50√2V
The correct Answer is:A
To solve the problem, we need to find the RMS value of the AC voltage applied to the electric iron, given that the heat produced is the same whether it is connected to an AC source or a 50 V constant voltage (DC).
1. Understanding the Heat Produced:
The heat produced (H) in an electric iron can be expressed in terms of power (P) and time (t):
H=P×t
For resistive heating, the power can also be expressed as:
P=V2R
where V is the voltage across the iron and R is its resistance.
2. Heat Produced with AC Voltage:
For an AC source, the peak voltage is denoted as Vpeak. The average power (and hence heat produced) over one cycle can be expressed as:
H1=V2peakR×t
However, since we are dealing with AC, we need to consider the RMS value of the voltage:
H1=V2rmsR×t
3. Heat Produced with DC Voltage:
For a DC source of 50 V, the heat produced can be expressed as:
H2=V20R×t
where V0=50V.
4. Equating the Heat Produced:
According to the problem, the heat produced in both cases is the same:
H1=H2
Substituting the expressions for H1 and H2:
V2rmsR×t=502R×t
The resistance R and time t can be canceled from both sides:
V2rms=502
5. Calculating the RMS Voltage:
Taking the square root of both sides gives:
Vrms=50V
Conclusion:
The RMS value of the AC voltage applied is:
50V
The heat produced (H) in an electric iron can be expressed in terms of power (P) and time (t):
H=P×t
For resistive heating, the power can also be expressed as:
P=V2R
where V is the voltage across the iron and R is its resistance.
For an AC source, the peak voltage is denoted as Vpeak. The average power (and hence heat produced) over one cycle can be expressed as:
H1=V2peakR×t
However, since we are dealing with AC, we need to consider the RMS value of the voltage:
H1=V2rmsR×t
For a DC source of 50 V, the heat produced can be expressed as:
H2=V20R×t
where V0=50V.
According to the problem, the heat produced in both cases is the same:
H1=H2
Substituting the expressions for H1 and H2:
V2rmsR×t=502R×t
The resistance R and time t can be canceled from both sides:
V2rms=502
Taking the square root of both sides gives:
Vrms=50V
The RMS value of the AC voltage applied is:
50V
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - C ) (Objective Type Questions) ( More than one option are correct)
2 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Try Yourself
15 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
When an a.c source is connected across a resistor
View SolutionA tube light of 60V,60W rating is connected across an AC source of 100V and 50Hz frequency. Then,
View SolutionA 110 V d.c. heater is used on an a.c source such that the heat produced is same as it produces when connected to 110 V dc in same time -intevals. What would be the r.m.s. value of the alternating voltage?
View SolutionProve that the current flowing through an ideal inductor connected across a.c. source, lags the voltage in phase by π2.
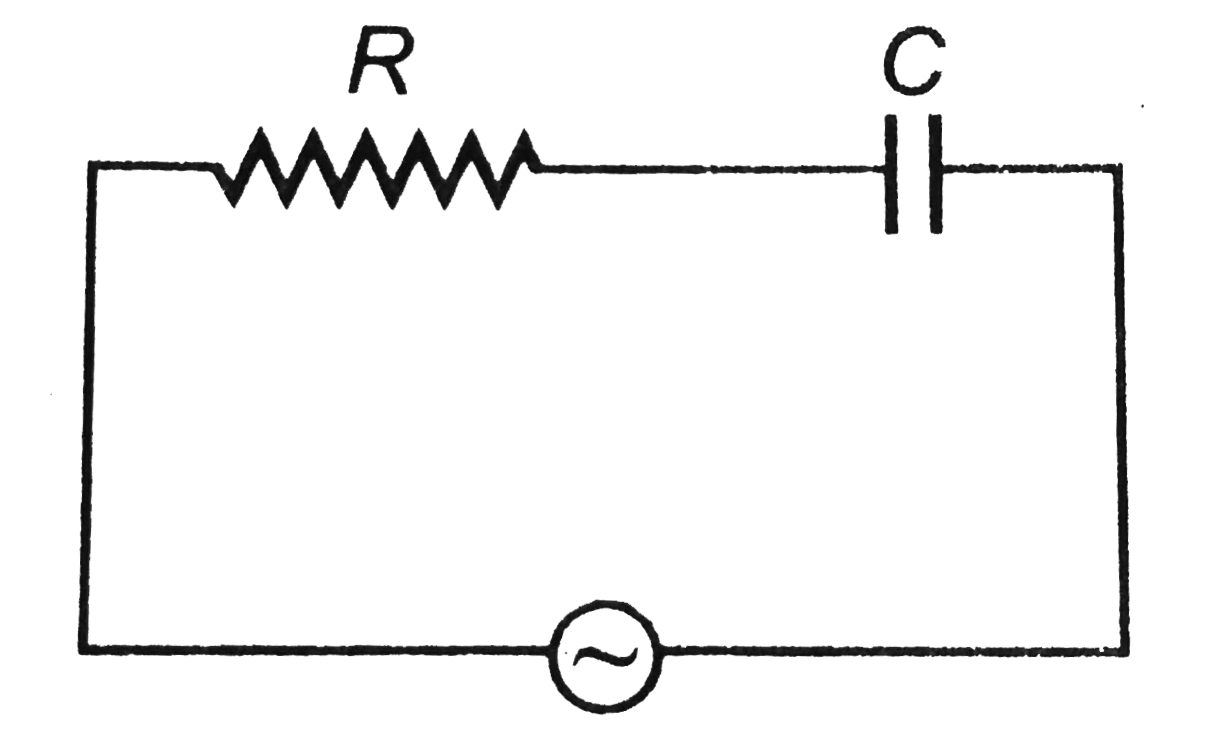
View SolutionA 50HzAC source of 20V is connected across R and C as shown in figure.
The voltage across R is 12V. The voltage across C is
View SolutionA coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
View SolutionAssertion : An inductor coil normally produces more current with DC source compared to an AC source of same value of rms voltage.
Reason : In DC source, applied voltage remains constant with time.
View SolutionA 50HzAC source of 20V is connected across R and C as shown in figureure.

The voltage across R is 12V. The voltage across C is
View SolutionAn LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionIn series LCR circuit, the voltages across R, L and C are shown in the figure. The voltage of applied source

View Solution
