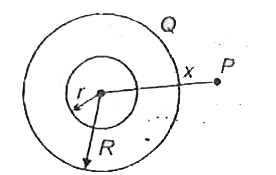
There are two concentric hollow conducting spherical shells of radii r and R(R>r). The charge on the outer shell is Q. What charge should be given to the inner shell, so that the potential at a point P , at a distance 2R from the common centre is zero ?
−QrR
−QRr
−2QRr
−Q)
The correct Answer is:D
To solve the problem, we need to determine the charge that should be given to the inner shell so that the potential at point P, located at a distance of 2R from the common center, is zero.
1. Understanding the Setup:
- We have two concentric hollow conducting spherical shells. The inner shell has a radius r and the outer shell has a radius R (where R>r).
- The outer shell has a charge Q, and we need to find the charge q on the inner shell.
2. Potential at Point P:
- Point P is located at a distance of 2R from the center of the shells.
- The potential V at point P due to a charged shell is given by the formula:
V=kQd
where k is Coulomb's constant, Q is the charge, and d is the distance from the center to the point where we are calculating the potential.
3. Calculating the Potential Due to Each Shell:
- The potential at point P due to the outer shell (charge Q):
Vouter=kQ2R
- The potential at point P due to the inner shell (charge q):
Vinner=kq2R
4. Setting Up the Equation for Zero Potential:
- For the total potential at point P to be zero, we set up the equation:
Vouter+Vinner=0
- Substituting the expressions for the potentials:
kQ2R+kq2R=0
5. Simplifying the Equation:
- We can factor out k2R (which is non-zero) from the equation:
k2R(Q+q)=0
- This implies:
Q+q=0
6. Finding the Charge on the Inner Shell:
- Rearranging gives:
q=−Q
- Therefore, the charge that should be given to the inner shell is −Q.
Final Answer:
The charge on the inner shell should be −Q.
- We have two concentric hollow conducting spherical shells. The inner shell has a radius r and the outer shell has a radius R (where R>r).
- The outer shell has a charge Q, and we need to find the charge q on the inner shell.
- Point P is located at a distance of 2R from the center of the shells.
- The potential V at point P due to a charged shell is given by the formula:
V=kQd
where k is Coulomb's constant, Q is the charge, and d is the distance from the center to the point where we are calculating the potential.
- The potential at point P due to the outer shell (charge Q):
Vouter=kQ2R
- The potential at point P due to the inner shell (charge q):
Vinner=kq2R
- For the total potential at point P to be zero, we set up the equation:
Vouter+Vinner=0
- Substituting the expressions for the potentials:
kQ2R+kq2R=0
- We can factor out k2R (which is non-zero) from the equation:
k2R(Q+q)=0
- This implies:
Q+q=0
- Rearranging gives:
q=−Q
- Therefore, the charge that should be given to the inner shell is −Q.
The charge on the inner shell should be −Q.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Two concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
View SolutionThere are two concentric conducting spherical shells of radii 10cm and 20cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThe radii of two concentric spherical conducting shells are r1andr2(>r1). The change on the oute shell is q. The charge on the inner shell which is connected to the earth is
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionThree concentric conducting spherical shells carry charges as : +4Q on the inner shell, −2Q on the middle shell and −5Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

View SolutionThree concentric conducting sphereical shells carry charges +4Q on the inner shell −2Q on the middle shel and +6Q on the outer shell. The charge on the inner surface of the outer shell is
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View Solutionthere are two concentric metallic shells of radii R and 2R, if outer shell is given charge q1 , then charge on surface of inner shell will be
View Solution
