A conducting rod PQ is rotated in a magnetic field B about an axis passing through point O as shown in figure. Then potential difference between P&Q is (ω : angular speed)
[Bω(b2−a2)]
Bωb22
Bωa22
[Bω2(b2−a2)]
The correct Answer is:D
To find the potential difference between points P and Q in a conducting rod PQ that is rotating in a magnetic field B about an axis through point O, we can follow these steps:
Step 1: Understand the setup
The conducting rod PQ is rotating in a magnetic field. The rotation creates a change in magnetic flux through the area swept by the rod, which induces an electromotive force (emf) between the ends of the rod.
Step 2: Determine the area swept by the rod
The area swept out by the rod when it rotates can be expressed as:
A=π(b2−a2)
where b is the distance from the axis of rotation to point Q, and a is the distance from the axis of rotation to point P.
Step 3: Calculate the magnetic flux
The magnetic flux Φ through the area swept by the rod is given by:
Φ=B⋅A=B⋅π(b2−a2)
where B is the magnetic field strength.
Step 4: Relate time to angular velocity
The time t taken for one complete rotation can be expressed in terms of angular velocity ω:
t=2πω
Step 5: Calculate the induced emf
The induced emf E is given by the rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux and the time period, we have:
E=−B⋅π(b2−a2)t=−B⋅π(b2−a2)2πω
This simplifies to:
E=B⋅ω(b2−a2)2
Step 6: Final expression for potential difference
Thus, the potential difference V between points P and Q is:
V=E=B⋅ω(b2−a2)2
Conclusion
The potential difference between points P and Q in the rotating conducting rod is:
V=B⋅ω(b2−a2)2
---
The conducting rod PQ is rotating in a magnetic field. The rotation creates a change in magnetic flux through the area swept by the rod, which induces an electromotive force (emf) between the ends of the rod.
The area swept out by the rod when it rotates can be expressed as:
A=π(b2−a2)
where b is the distance from the axis of rotation to point Q, and a is the distance from the axis of rotation to point P.
The magnetic flux Φ through the area swept by the rod is given by:
Φ=B⋅A=B⋅π(b2−a2)
where B is the magnetic field strength.
The time t taken for one complete rotation can be expressed in terms of angular velocity ω:
t=2πω
The induced emf E is given by the rate of change of magnetic flux:
E=−dΦdt
Substituting the expression for magnetic flux and the time period, we have:
E=−B⋅π(b2−a2)t=−B⋅π(b2−a2)2πω
This simplifies to:
E=B⋅ω(b2−a2)2
Thus, the potential difference V between points P and Q is:
V=E=B⋅ω(b2−a2)2
The potential difference between points P and Q in the rotating conducting rod is:
V=B⋅ω(b2−a2)2
Topper's Solved these Questions
Similar Questions

A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA conducting circular ring is rotated with angular velocity ω about point A as shown in figure. Radius of ring is a find
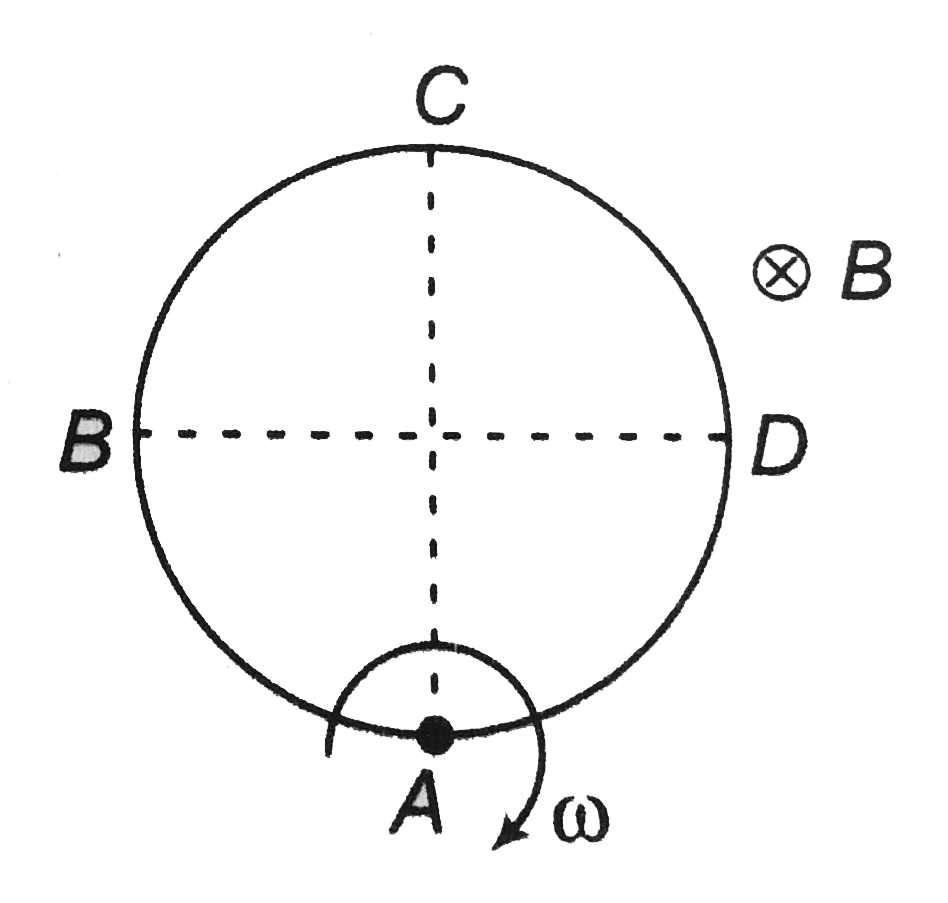
a. potential difference between points A and C
b. potential difference between the points A and D.
View SolutionA metallic rod of length l is hinged at the point M and is rotating about an axis perpendicular to the plane of paper with a constant angular velocity ω. A uniform magnetic field of intensity B is acting in the region (as shown in the figure) parallel to the plane of paper. The potential difference between the points M and N

View SolutionA metallic rod of length l is hinged at the point M and is rotating about an axis perpendicular to the plane of paper with a constant angular velocity ω. A uniform magnetic field of intensity B is acting in the region (as shown in the figure) parallel to the plane of paper. The potential difference between the points M and N

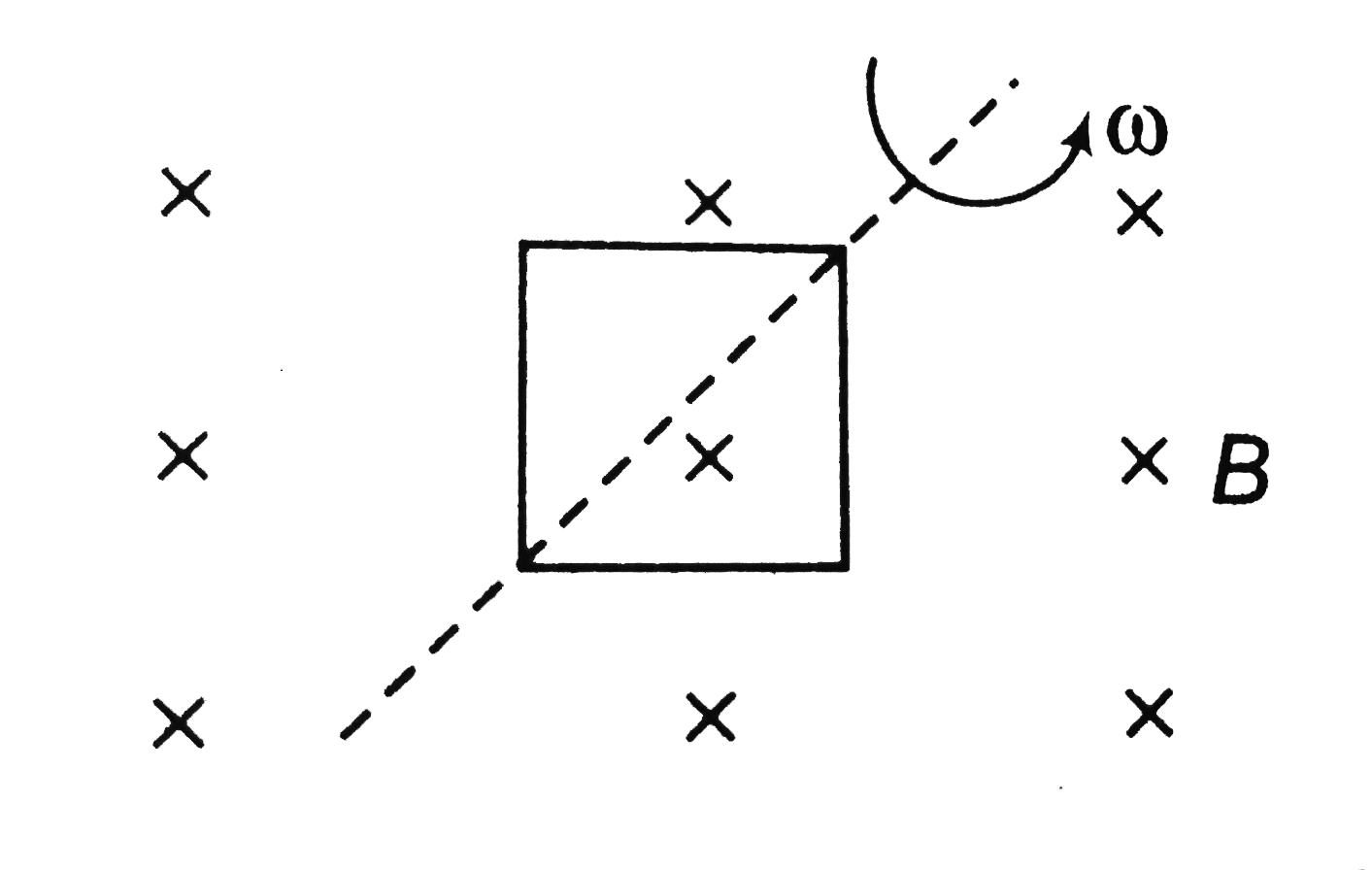
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
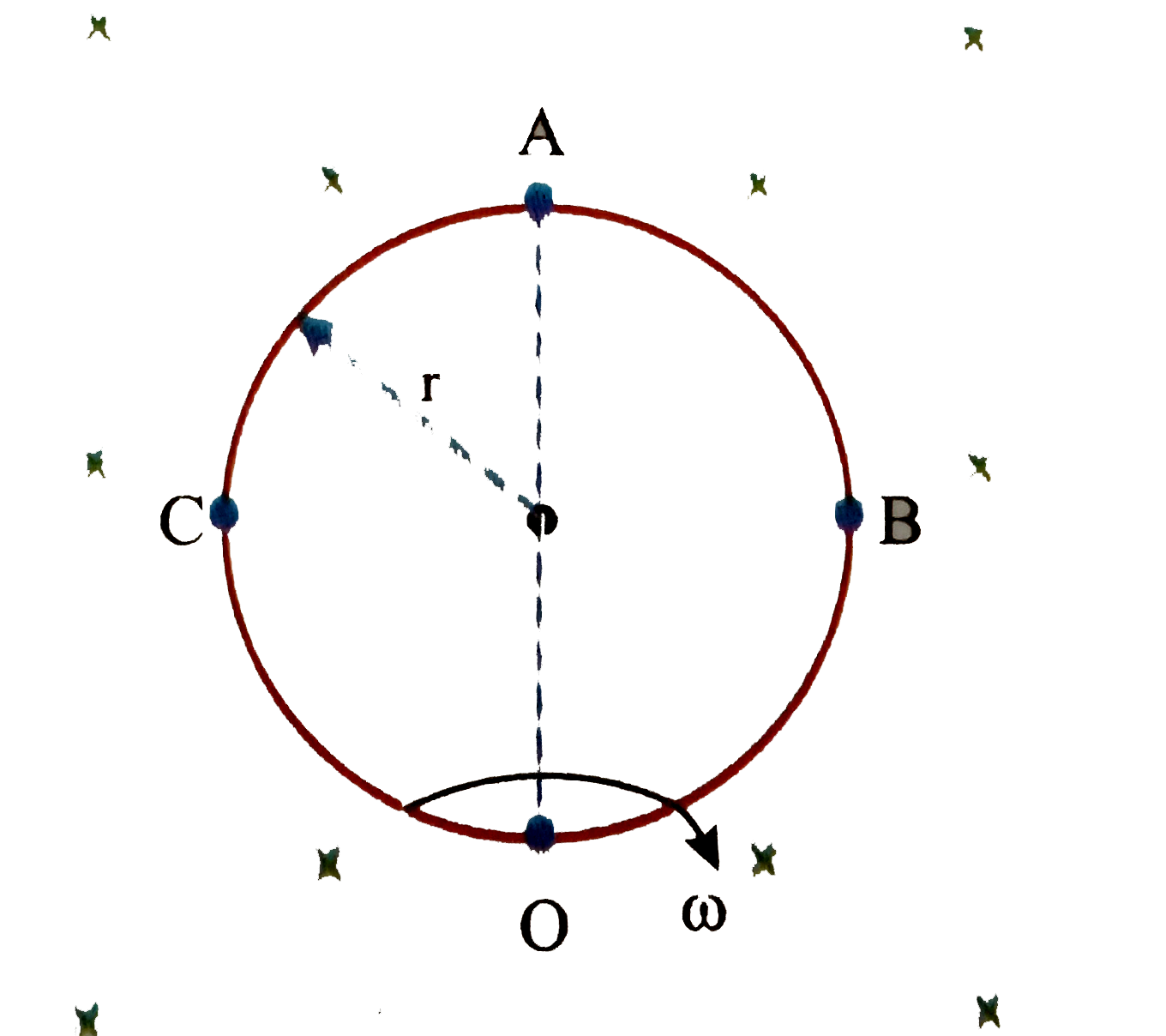
View SolutionIn figure, there is conducting ring having resistance R placed in the plane of paper in a uniform magnetic field B0. If the rings is rotating in the plane of paper about an axis passing through point O and perpendicular to the plane of paper with constant angular speed ω in clockwise direction, then
View SolutionA hollow non conducting sphere of radius R has a positive charge q uniformly distributed on its surface. The sphere starts rotating with a constant angular velocity 'ω' about an axis passing through center of sphere, as shown in the figure. Then the net magnetic field at center of the sphere is

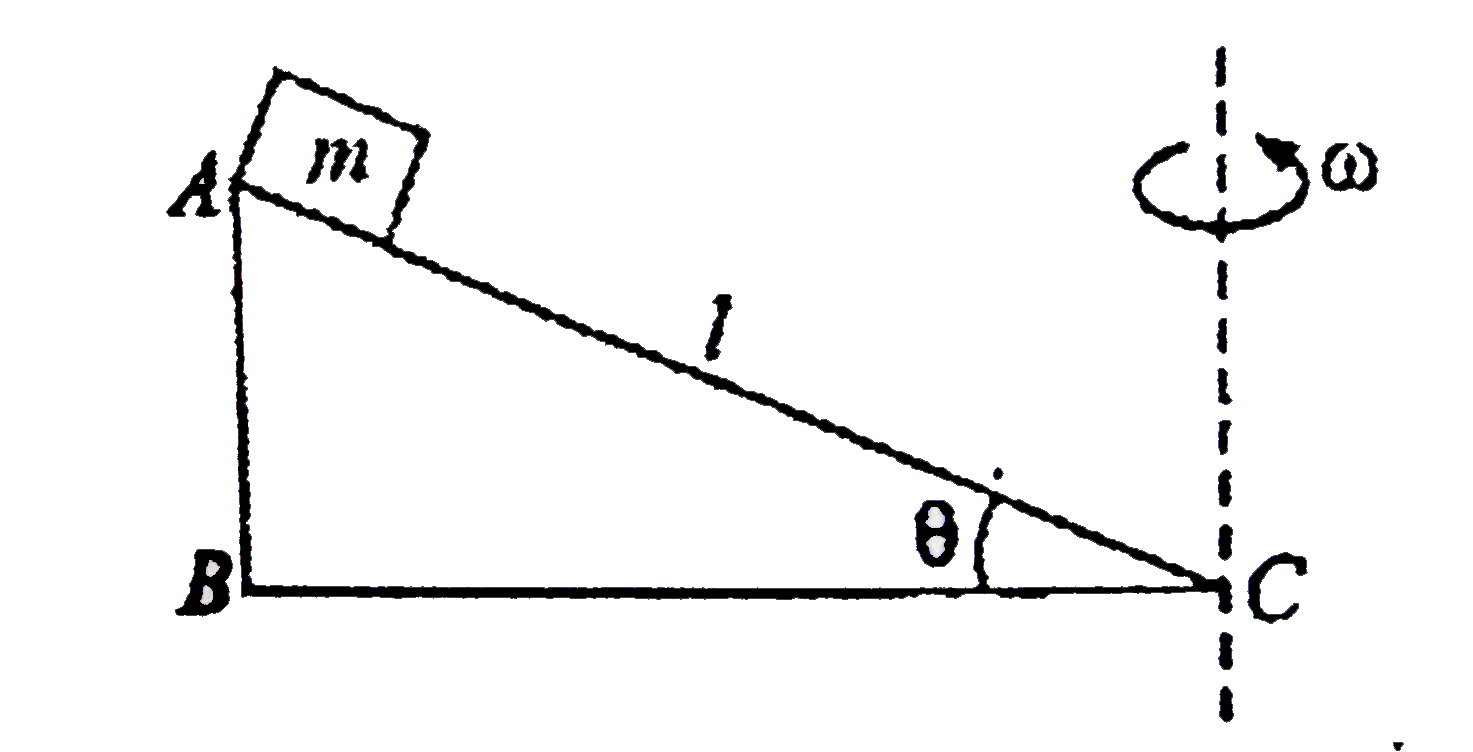
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View Solution
