All the pulleys are ideal, string is massless then rate of work done by gravity at the given instant is (−x×102)W then calculate x :
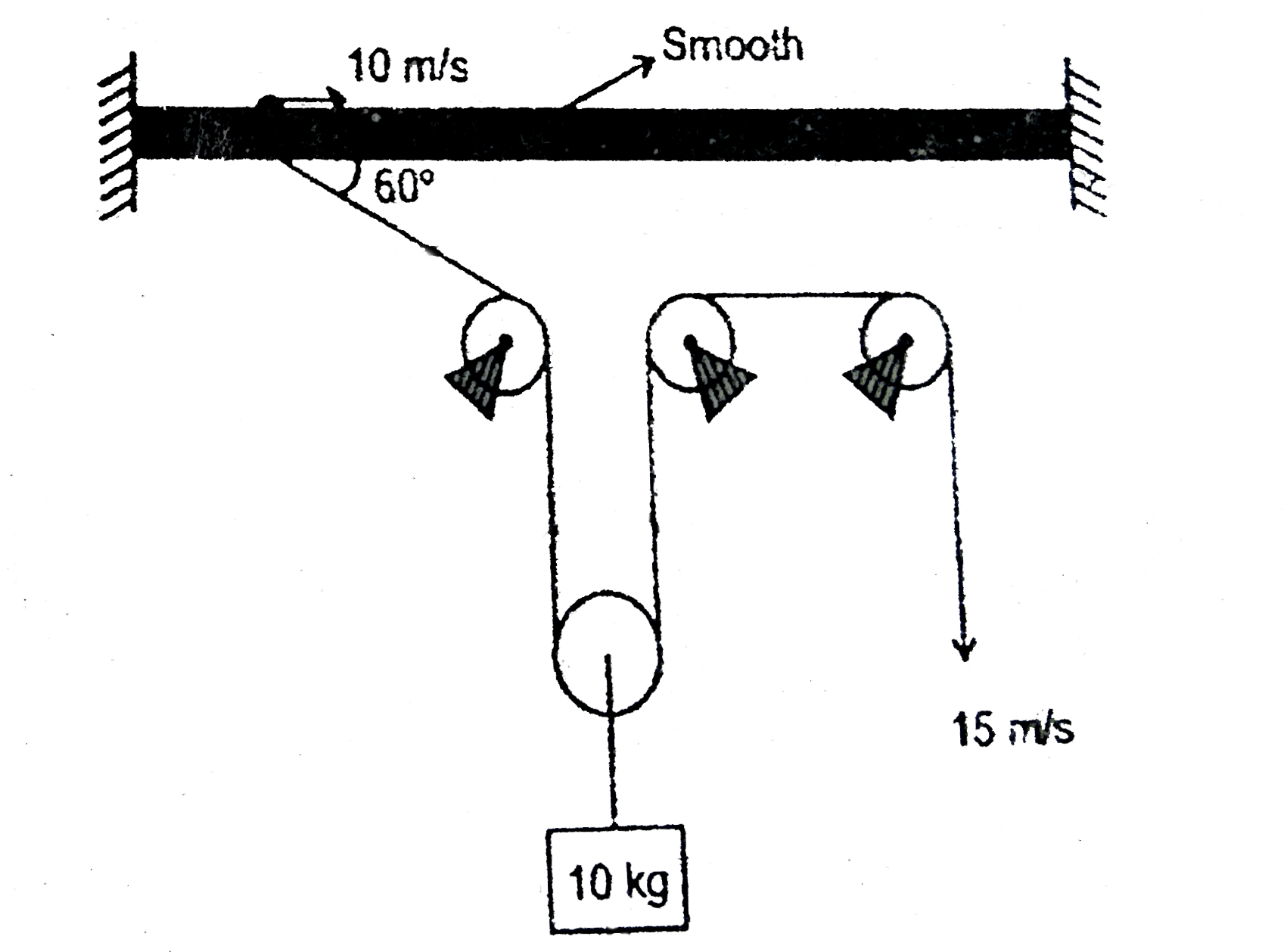
The correct Answer is:5
vp=−5+152=5m/s
P=→F.→V=−mgV
=−100×5=−500W
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS SEC - 2
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
If pulley is ideal and string is massless then reading of weighing machine is 5x3kg then calculate x.:(g=10m/s2)

View SolutionA diatomic ideal gas is expanded at constant pressure. If work done by the system is 10 J then calculated heat absorbed.
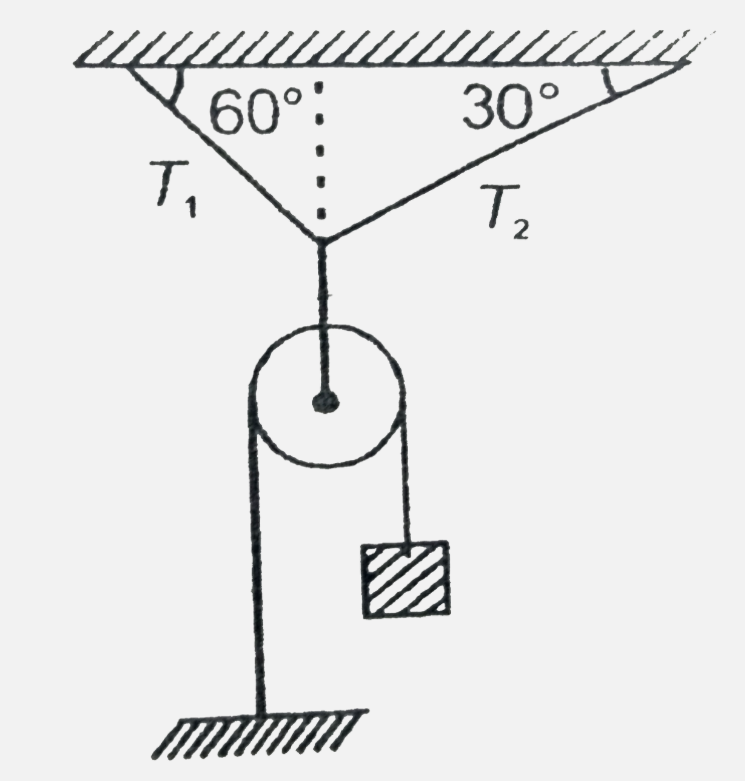
View SolutionIf pulley and all strings as shown are massless, then tension T2=100N . Calculate weight of the block ( g = 10m/s2)
View SolutionTwo blocks of masses 10 kg and 9 kg are connected with light string which is passing over an ideal pulley as shown in figure. If system is released from rest then the acceleration of 9 kg block at the given instant is about (Assume all the surfaces are smooth and g=10ms2)
View SolutionFor the reaction x+2y→3z the rate at a given instant of time can be represented as:
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 is
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 is
View SolutionTwo moles of an ideal gas undergoes the following process. Given that (∂P∂T)Vis x×10+y, then calculate the value of (x + Y)
View SolutionA sample of mono-atomic ideal gas is taken through a cyclic process ABCDA. A graph is plotted in which heat exchanged by the gas upto an instant is shown on x-axis and work done by the gas upto that instant is shown on y-axis.
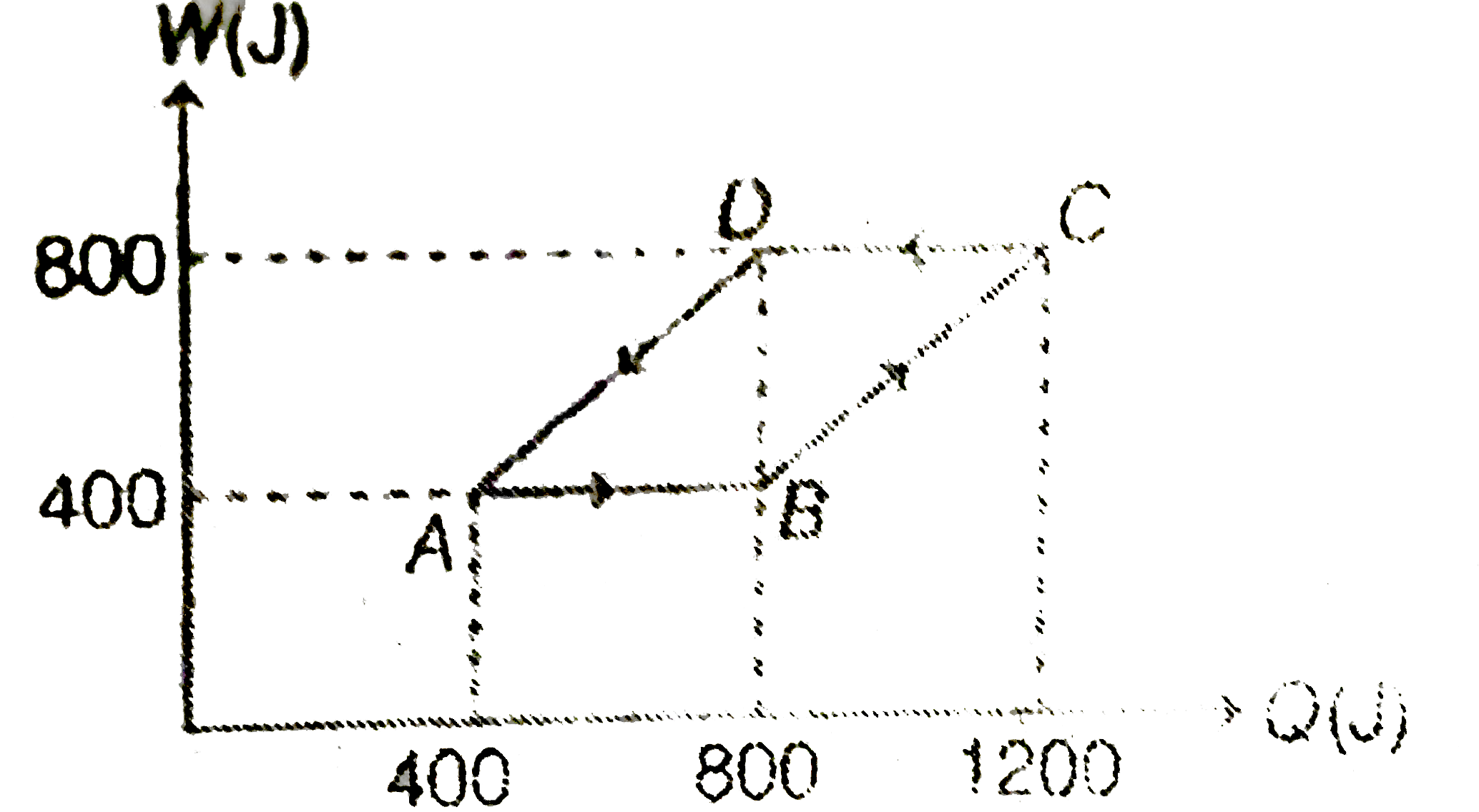
The given cyclic process can be represented on a pressure-volume graph as:
View SolutionIn the arrangement shown in Fig. 7.100 , mass can be hung from a string with a linear mass density of 2×10−3kg/m that passes over a light pulley . The string is connected to a vibrator of frequency 700Hz and the length of the string between the vibrator and the pulley is 1m.

The string is set into vibrations and represented by the equation y=6sin(πx10)cmcos(14×103πt) where x ane y are in cm , and t in s, the maximum displacement at x=5m from the vibrator is
View Solution
