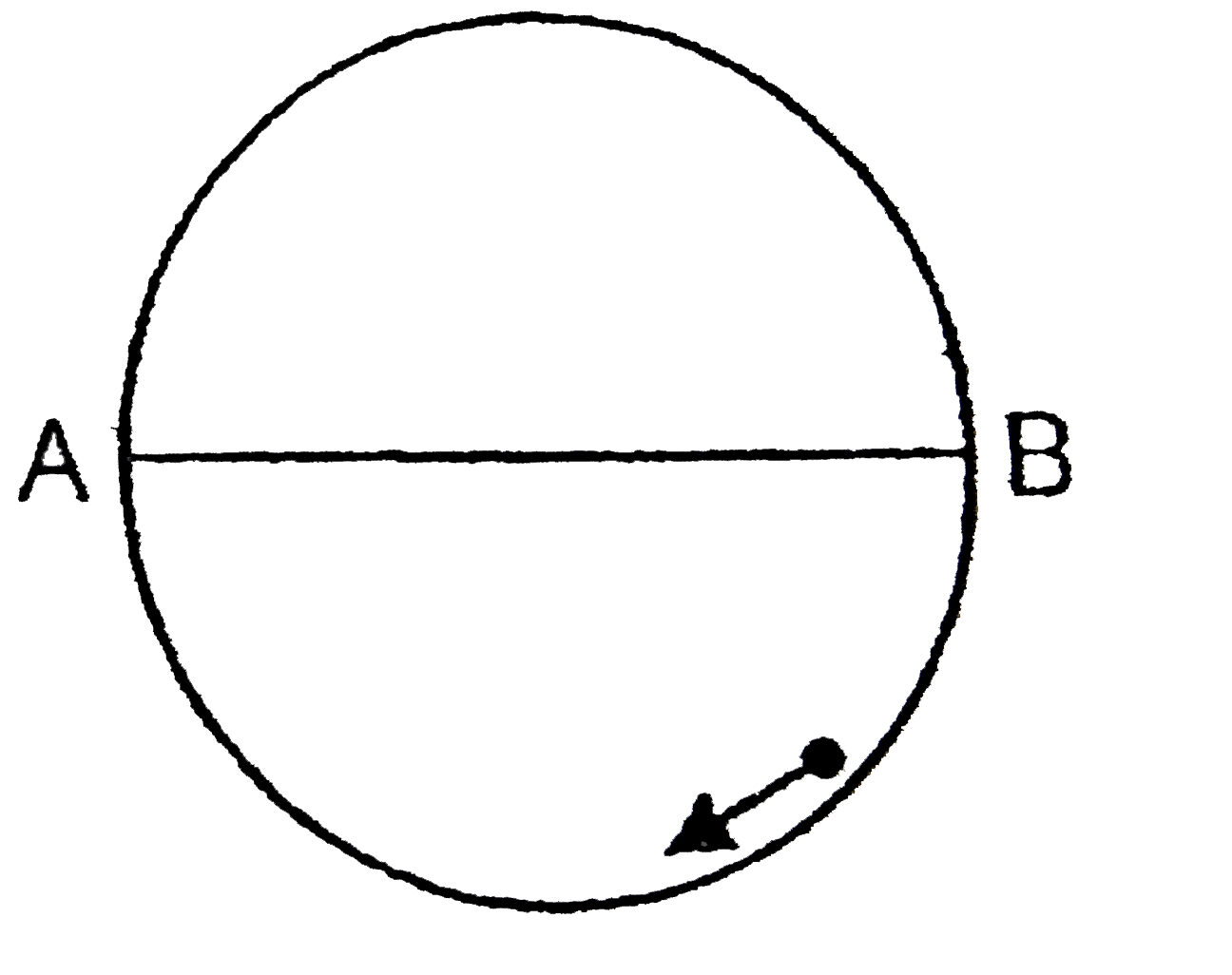
A particle of mass m oscillates inside the smooth surface a fixed pipe of radius R. The axis of the pipe is horizontal and the particle moves from B to A and back. At an instant the kinetic energy of the particle is K (say at position of the particle shown in figure ). Then choose the correct value of force applied by particle on the pipe at this instant.
KR
5KR
3KR
2KR
The correct Answer is:C
Let velocity of particle at point P be v.
From conservation of mechanical energy
12.mv2=K=mgh
Let N be the normal reaction between the particle and the pipe at this instant.
Then N−mgsinθ=mv2R
But, mv2R=2KR and sinθ=hR
Hence, N=mg(hR)+2KR=KR+2KR
('∴K=mgh)
Hence, N=3KR= force on the pipe.

Topper's Solved these Questions
Similar Questions
A particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B. At given instant the kinetic energy of the particle is K. Then the force applied by particle on the shell at this instant is :−
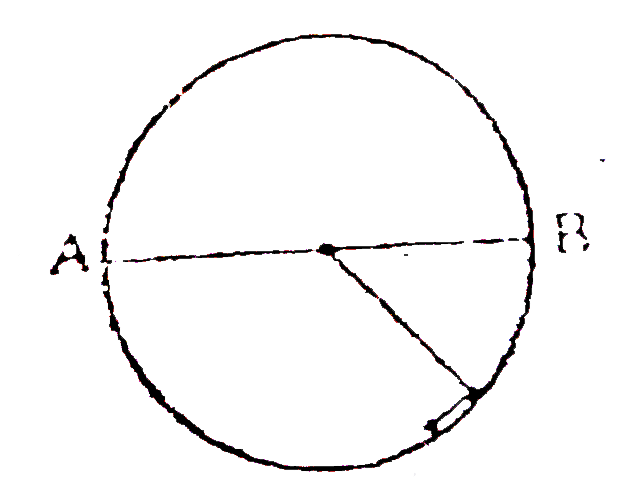 View Solution
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure

The magnitude of force acting on particle at x = 9 misView SolutionA particle of mass m is moved from A to B as show in figure. Then potential energy of the the particle
 View Solution
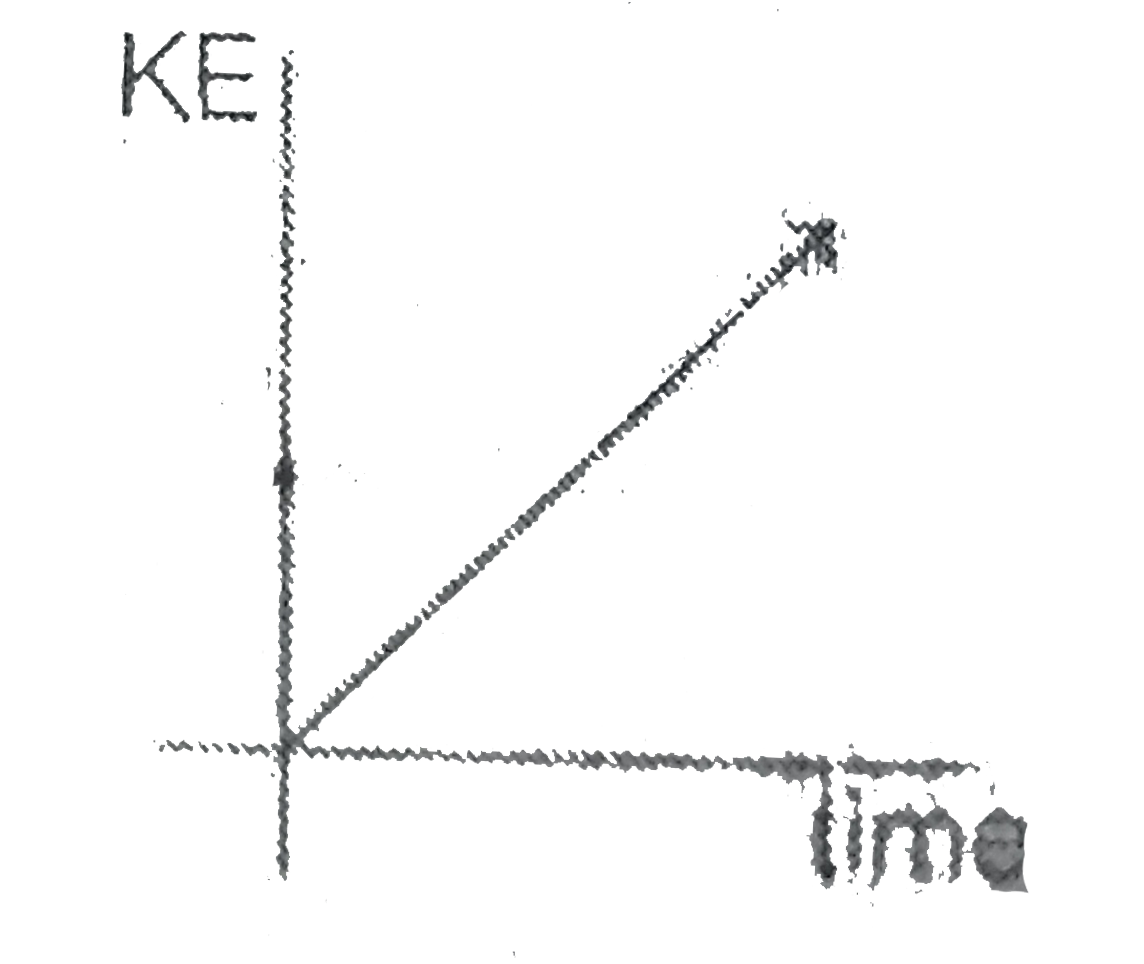
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
 View Solution
View SolutionThe variation of force (F) acting on a particle of mass 800 g with position (x) is as shown in figure. The time period of oscillation of the particles is
View SolutionA particle initially at rest is displaced from x=−10 m to x=+10m, under a force F as shown in the figure.
Now the kinetic energy vs position graph of the particle is
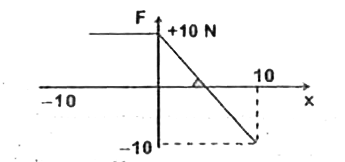 View Solution
View SolutionIn the figure shown the potential energy U of a particle is plotted its position 'x' from origin. Then which of the following statement is correct A particle at :
 View Solution
View SolutionA particle of mass m is kept on a fixed, smooth sphere of radius R at a position, where the radius through the particle makes an angle of 30 ∘ with the vertical. The particle is released from this position. (a) What is the force exerted by the sphere on the particle just after the release? (b) Find the distance traveled by the particle before it leaves contact with the sphere.
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionA particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is
 View Solution
View Solution

