A moving perticle of mass m is acted upon by five forces →F1,→F2,→F3,→F4 and →F5. Forces →F2 and →F3 are conservative and their potential energy funcations are U and W respectively. Speed of the particle changes from Va to Vb when it moves from position a to b. Choose the correct option :
Sum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−Wa
Sum of work done by →F1,→F4 and →F5=Ub−Ua+Wb−Wa+12m(V2b−V2a)
Sum of work done by all five forces =12m(V2b+V2a)
Sum of work done by →F2 and →F3=(Ub+Wb)−(Ua+Wa)
The correct Answer is:B
To solve the problem, we will apply the work-energy theorem and analyze the forces acting on the particle. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Work-Energy Theorem
The work-energy theorem states that the total work done on an object is equal to the change in its kinetic energy. Mathematically, this can be expressed as:
Wtotal=ΔKE=KEf−KEi
where KEf is the final kinetic energy and KEi is the initial kinetic energy.
Step 2: Write the Expression for Total Work Done
Given that the particle is acted upon by five forces →F1,→F2,→F3,→F4,→F5, the total work done by these forces can be expressed as:
Wtotal=W1+W2+W3+W4+W5
Step 3: Calculate the Change in Kinetic Energy
The kinetic energy of the particle at position a is given by:
KEi=12mV2a
The kinetic energy at position b is:
KEf=12mV2b
Therefore, the change in kinetic energy is:
ΔKE=12mV2b−12mV2a
Step 4: Relate Work Done to Change in Kinetic Energy
By substituting the expression for change in kinetic energy into the work-energy theorem, we have:
Wtotal=12mV2b−12mV2a
Step 5: Analyze the Work Done by Conservative Forces
For the conservative forces →F2 and →F3, the work done can be expressed in terms of potential energy:
W2=−ΔU=−(Ub−Ua)=Ua−Ub
W3=−ΔW=−(Wb−Wa)=Wa−Wb
Thus, the total work done by the conservative forces is:
W2+W3=(Ua−Ub)+(Wa−Wb)
Step 6: Calculate Work Done by Non-Conservative Forces
The work done by the non-conservative forces →F1,→F4,→F5 can be expressed as:
W1+W4+W5=Wtotal−(W2+W3)
Step 7: Substitute and Rearrange
Substituting the expressions for Wtotal and W2+W3:
W1+W4+W5=(12mV2b−12mV2a)−((Ua−Ub)+(Wa−Wb))
This simplifies to:
W1+W4+W5=12mV2b−12mV2a+Ub−Ua+Wb−Wa
Conclusion
Thus, we have derived the expressions for the work done by the forces acting on the particle and can choose the correct options based on the analysis.
The work-energy theorem states that the total work done on an object is equal to the change in its kinetic energy. Mathematically, this can be expressed as:
Wtotal=ΔKE=KEf−KEi
where KEf is the final kinetic energy and KEi is the initial kinetic energy.
Given that the particle is acted upon by five forces →F1,→F2,→F3,→F4,→F5, the total work done by these forces can be expressed as:
Wtotal=W1+W2+W3+W4+W5
The kinetic energy of the particle at position a is given by:
KEi=12mV2a
The kinetic energy at position b is:
KEf=12mV2b
Therefore, the change in kinetic energy is:
ΔKE=12mV2b−12mV2a
By substituting the expression for change in kinetic energy into the work-energy theorem, we have:
Wtotal=12mV2b−12mV2a
For the conservative forces →F2 and →F3, the work done can be expressed in terms of potential energy:
W2=−ΔU=−(Ub−Ua)=Ua−Ub
W3=−ΔW=−(Wb−Wa)=Wa−Wb
Thus, the total work done by the conservative forces is:
W2+W3=(Ua−Ub)+(Wa−Wb)
The work done by the non-conservative forces →F1,→F4,→F5 can be expressed as:
W1+W4+W5=Wtotal−(W2+W3)
Substituting the expressions for Wtotal and W2+W3:
W1+W4+W5=(12mV2b−12mV2a)−((Ua−Ub)+(Wa−Wb))
This simplifies to:
W1+W4+W5=12mV2b−12mV2a+Ub−Ua+Wb−Wa
Thus, we have derived the expressions for the work done by the forces acting on the particle and can choose the correct options based on the analysis.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
Arrange nucleophilicity of given species in decreasing order:
(1) CH3−өCH2
(2) CH3−өO
(3) өNH2
(4) өF
View SolutionA body placed in free space, is simultaneously acted upon by three forces −→F1,−→F2 and −→F3. The body is in equilibrium and the forces −→F1 and −→F2 are known ot be 36 N due north and 27 N due east respectively. Which of the following best describes the force −→F3?
View SolutionXe+F21:20−−→XH2O−−→YH2O−−→ZH2O−−→XeO3
Select correct option(s) for X, Y, Z and given chemical change:
View SolutionXe+F21:20−−→XH2O−−→YH2O−−→ZH2O−−→XeO3
Select correct option(s) for X, Y, Z and given chemical change:
View SolutionIf →F is force vector, →v is velocity , →a is acceleration vector and →r vector is displacement vector w.r.t. mean position than which of the following quantities are always non-negative in a simple harmonic motion along a straight line ?
View SolutionABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

View SolutionThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
View SolutionIdentify A to F :
ALiAlH4−−−→C2H5OHPBr3−−→BKCN−−→CD−−→C3H7NH2HNO2−−−→E[O]−−−−−−−−−−→K2Cr2O7/H+F
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
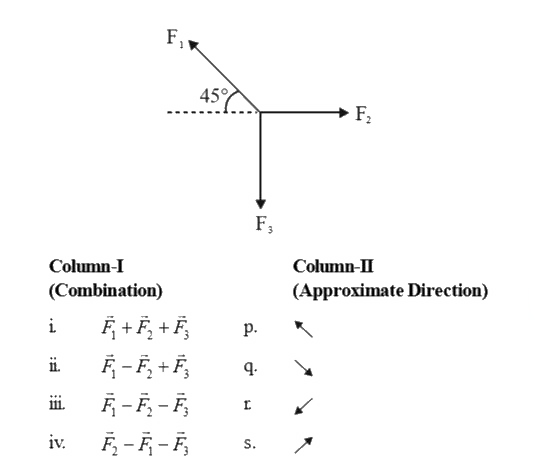
Now match the given columns and select the correct option from the codes given below.
View Solution(a). CuSO4.5H2O100∘−−→(A)230∘−−→(B)800∘−−→(C)+(D)
(b). AgNO3redhot−−−→(E)+(F)+O2
View Solution