Question

A uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is $\frac{3mg}{K}$, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).

Options

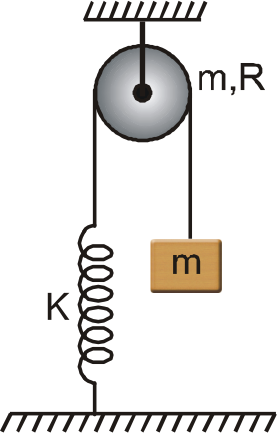
A. Acceleration of block just after is released is `(4g)/(3)`
B. Tension in the string continuosly increases till extension in the spring reaches maximum value
C. maximum extension in the spring is `(2mg)/(K)`
D. Maximum extension in the spring is `(mg)/(K)`

Answer

A::B::C

Explanation

For disc, from torque equation
`3 mg R - TR = (mR^(2))/(2) alpha` ….(i)
By application of Newtion's second law on block we get,

`T - mg = mg` ….(ii)
where `a = R alpha` …..(iii)
solving `a = (4g)/(3)`