For given spring mass system, if the time period of small oscillations of block about its mean position is π√nmK, then find n. Assume idela conditions. The system is in vertical plane and take K1=2K,K2=K.
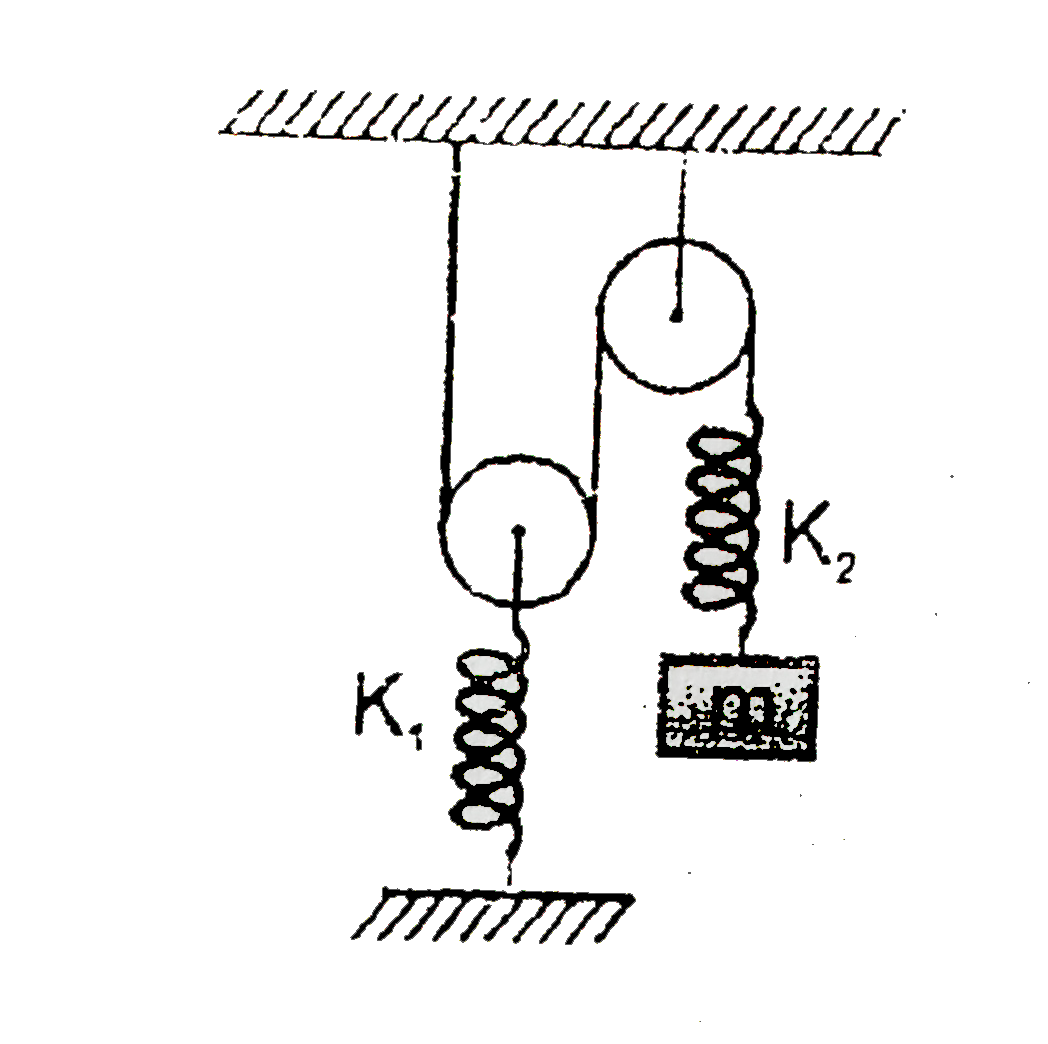
The correct Answer is:12
Step by step video & image solution for For given spring mass system, if the time period of small oscillations of block about its mean position is pisqrt((nm)/(K)), then find n. Assume idela conditions. The system is in vertical plane and take K_(1) = 2K, K_(2) = K. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - III
Explore 12 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - II
Explore 36 Videos
- SEMICONDUCTORSBook:RESONANCE ENGLISHChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
Similar Questions
Spring mass system is shown in figure. find the time period of vertical oscillations. The system is in vertical plane.

View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.

View SolutionIf the angular frequency of small oscillations of a thin uniform vertical rod of mass m and length l hinged at the point O (Fig.) is √nl, then find n. The force constant for each spring is K/2 and take K=2mgl. The springs are of negiligible mass. (g=10m/s2)
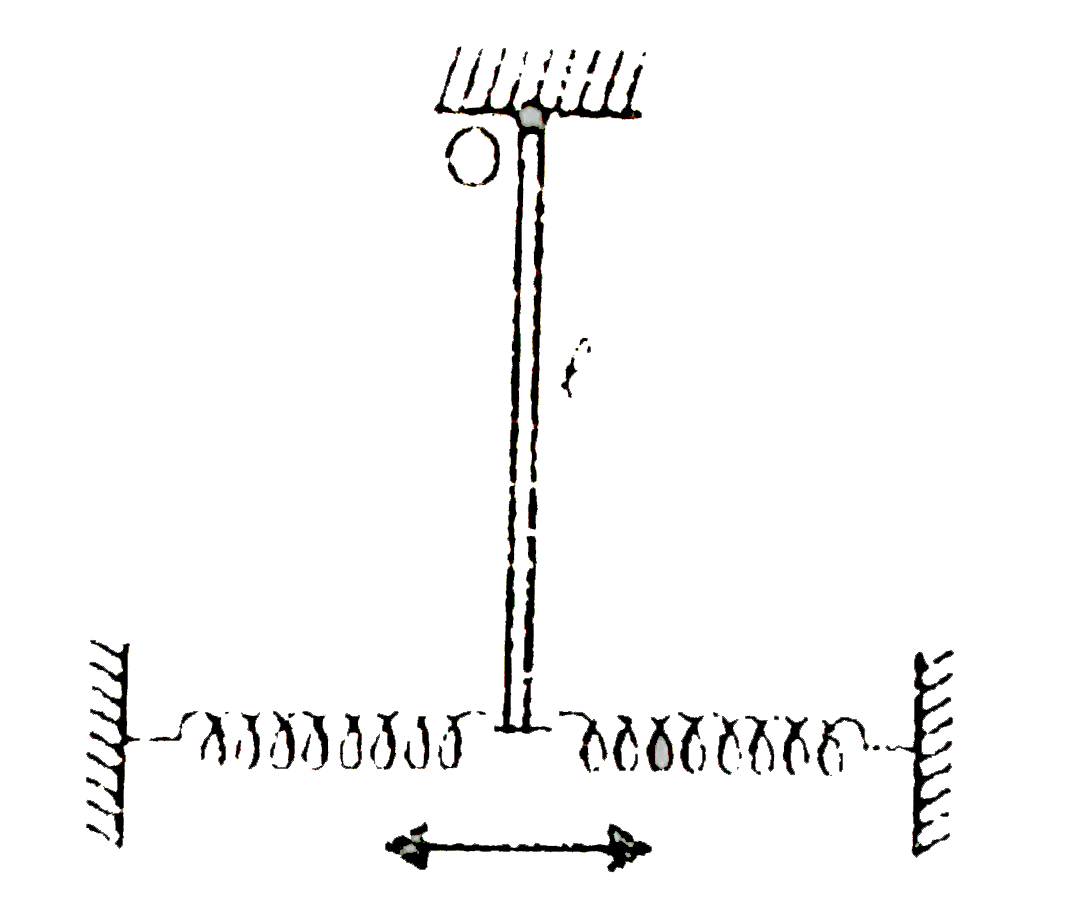
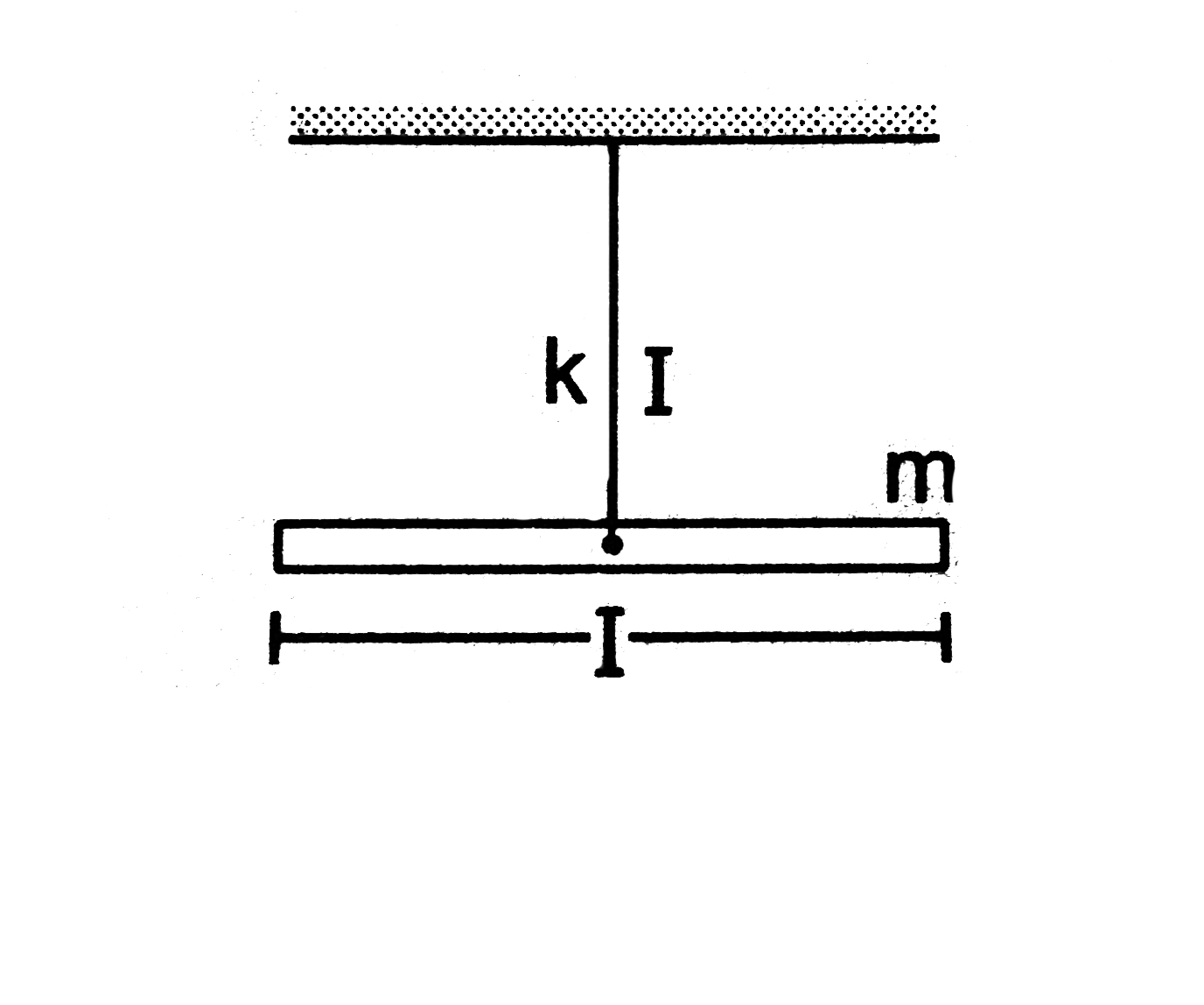
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
View SolutionA particle of mass m in suspended at the lower end of a thin negligible mass. The upper end of the rod is free to rotate in the plane of the page about a horizontal axis passing through the point O. The spring is underformed when the rod is vertical as shown in fig. If the period of oscillation of the system is π√Ln, when it is slightly displaced from its mean position then find n. Take k=9mgLl2 and g=10m/s2.

View Solution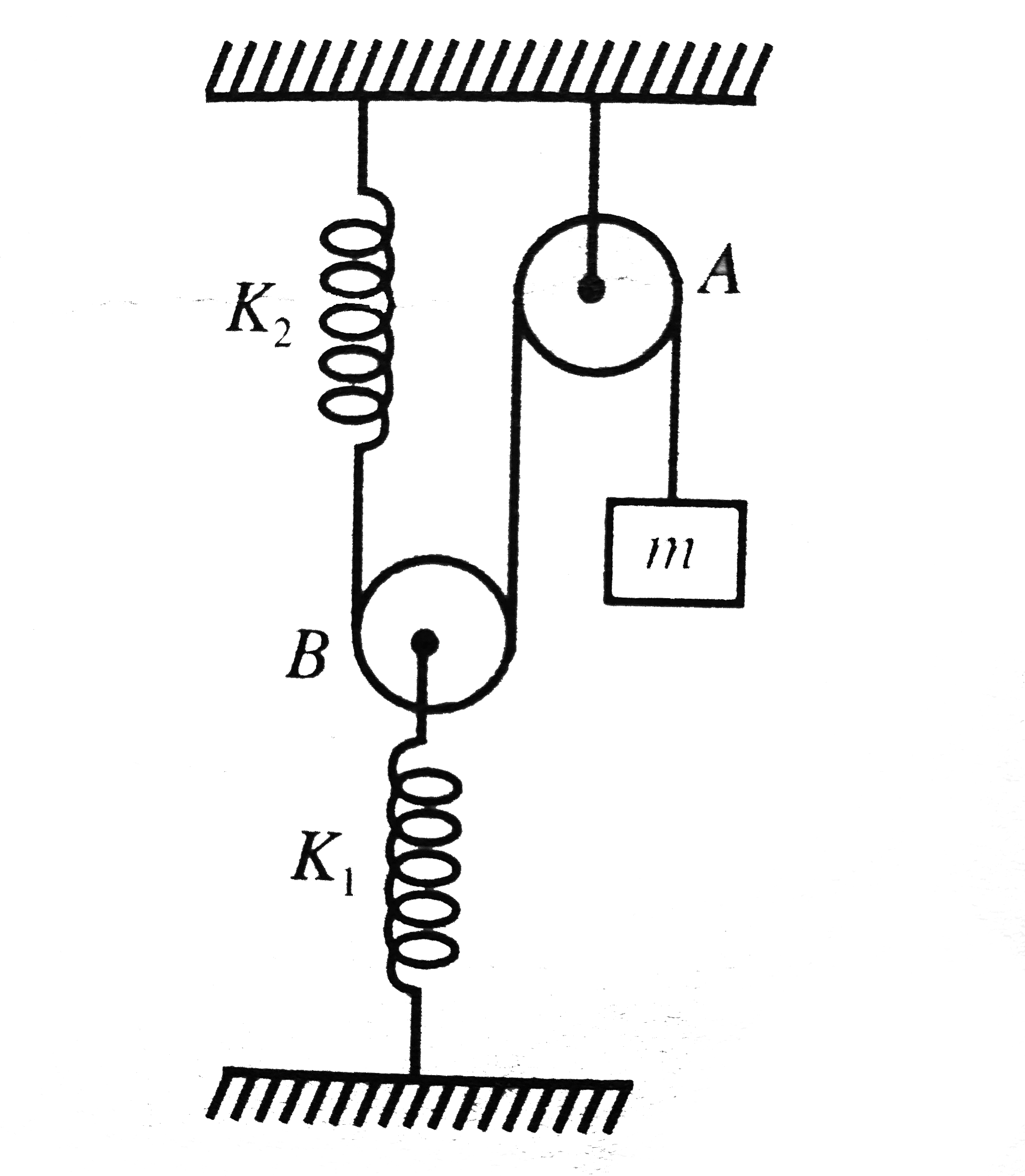
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View SolutionA: If a spring block system, oscillating in a vertical plane is made to oscillate on a horizontal surface, the time period will remain same.
R: The time period of spring block system does not depend on g.
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionDerive an experession for the period of oscillation of a mass attached to a spring executing simple harmonic motion. Given that the period of oscillation depends on the mass m and the force constant k, where k is the force required to stretch the spring by unit length?
View Solution