Question

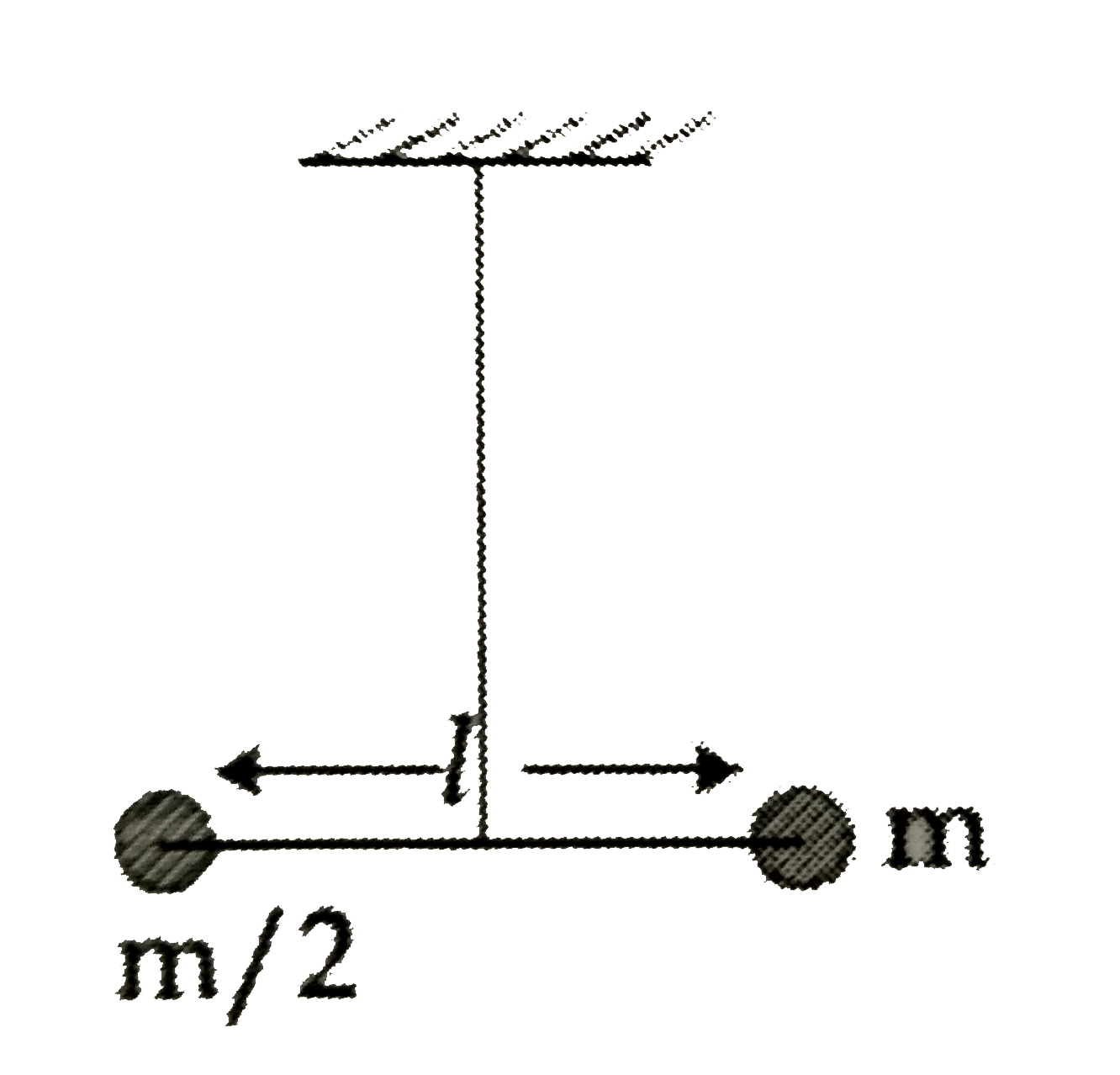
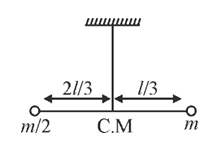
Two masses m and ${\displaystyle \frac{m}{2}}$ are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is ${\displaystyle \tau =k\theta }$ for angular displacement ${\displaystyle \theta }$. If the rod is rotated by ${\displaystyle {\theta }_0}$ and released, the tension in it when it passes through its mean position will be :

Options

A. `3ktheta_(0)^(2)/1`
B. `ktheta_(0)^(2)/21`
C. `2ktheta_(0)^(2)/1`
D. `ktheta_(0)^(2)/1`

Answer

D

Explanation

Iprop=-k^(theta)
`[m/2(21/3)^(2)+m(1/3)^(2)]prop=-ktheta`
`(mI^(2))/(3)prop=-ktheta therefore omega^(2)=(3k)/(mI^(2))`
Angular velocity at mean `omega_(0)=theta_(0)omega=theta_(0)sqrt((3k)/mI^(2))`
`T=momega_(0)^(2)(l)/(3)=m" "theta_(0)^(2)(3k)/(ml^(2))(l)/(3)=(ktheta_(0)^(2))/(l)`