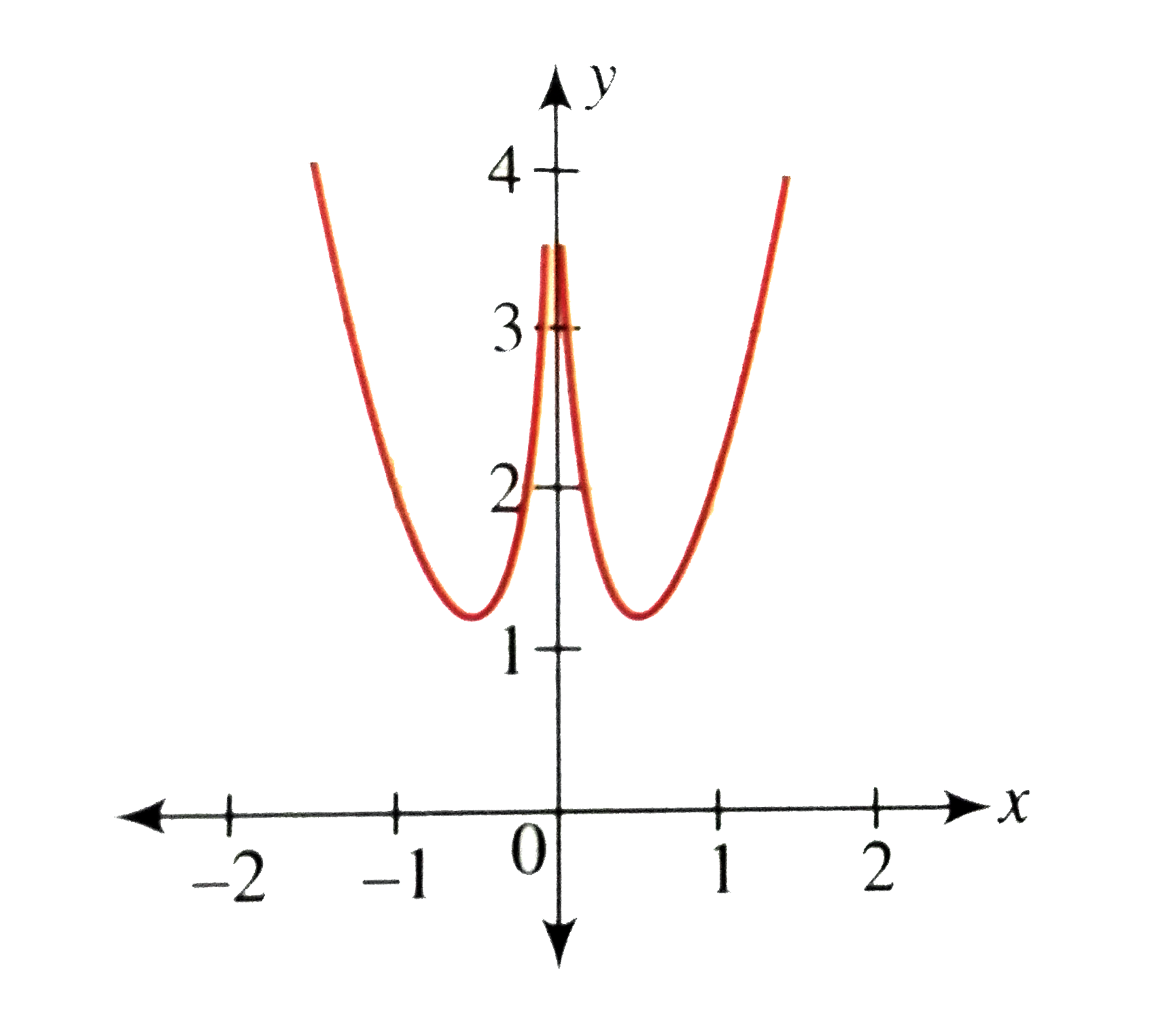
Draw the graph of the function f(x)=2x2−loge|x|Solution in Tamil
We have f(x)=2x2−loge|x|,x≠0
Clearly, f(x) is an even function, hence its graph is symmetrical about the y-axis.
limx→0+(2x2−loge|x|)=∞ and limx→±∞(2x2−loge|x|)=∞ (as difference between the value of 2x2 and ln|x| is infinite, loge|x| increases very slowly, but 2x2 increases faster)
Also f′(x)=4x−1x=4x2−1x
f′(x)=0⇒x=±12
From the limiting values of the function at x=0 and at inifinity, we can conclude that x=±12 are points of minima.
From the above discussion, the graph of the function is as shown in the following figure.
Topper's Solved these Questions
Similar Questions
Draw the graph of y=sin2x−cosx
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionSolve: (x+2)3=2x(x2−1)
View SolutionDraw the graph of the function f(x)=2x-|x|
View SolutionDraw the graph of f(x)=[logex],e−2<x<10, where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
View SolutionDraw the graph of the function f(x)=2x2−loge|x|
View SolutionDraw the graph of y=(logex)2
View SolutionDraw the graph of the function, f(x) = 2x - 5.
View SolutionDraw the graph of the function, f(x)=ex.
View SolutionDraw the graph of the function, f(x)=logex(x>0).
View SolutionDraw the graph of f(x)=[logex],e−2<x<10, where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=loge(−x),−logex,y=|logex|,y=loge|x| and y=|loge|x|| transforming the graph of y=logex.
View SolutionDraw the graph of the function f(x)=2x2−loge|x|
View SolutionDraw the graph of y=(logex)2
View Solution
