State whether the statements are true (T) or (F) false.
If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
To determine whether the statement "If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon" is true or false, we will go through the necessary calculations step by step.
1. Understand the formulas for the sum of interior and exterior angles:
- The sum of the interior angles of a polygon with n sides is given by the formula:
Sum of interior angles=(n−2)×180∘
- The sum of the exterior angles of any polygon is always:
Sum of exterior angles=360∘
2. Set up the equation based on the statement:
- According to the statement, if the sum of the interior angles is double the sum of the exterior angles, we can express this as:
Sum of interior angles=2×Sum of exterior angles
- Substituting the formulas, we have:
(n−2)×180∘=2×360∘
3. Simplify the equation:
- Simplifying the right side:
(n−2)×180∘=720∘
- Now, divide both sides by 180∘:
n−2=720180
- This simplifies to:
n−2=4
4. Solve for n:
- Adding 2 to both sides gives:
n=4+2=6
5. Conclusion:
- Since n=6, this means the polygon is a hexagon. Therefore, the statement is true.
Final Answer:
The statement is True (T).
- The sum of the interior angles of a polygon with n sides is given by the formula:
Sum of interior angles=(n−2)×180∘
- The sum of the exterior angles of any polygon is always:
Sum of exterior angles=360∘
- According to the statement, if the sum of the interior angles is double the sum of the exterior angles, we can express this as:
Sum of interior angles=2×Sum of exterior angles
- Substituting the formulas, we have:
(n−2)×180∘=2×360∘
- Simplifying the right side:
(n−2)×180∘=720∘
- Now, divide both sides by 180∘:
n−2=720180
- This simplifies to:
n−2=4
- Adding 2 to both sides gives:
n=4+2=6
- Since n=6, this means the polygon is a hexagon. Therefore, the statement is true.
The statement is True (T).
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
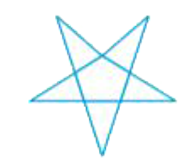 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
The sum of interior angles and the sum of exterior angles taken in an order are equal in case of quadrilaterals only.
View SolutionState whether the statements are true (T) or (F) false.
Triangle is a polygon whose sum of exterior angles is double the sum of interior angles.
View SolutionState whether the statements are true (T) or (F) false.
Sum of all the angles of a quadrilateral is 180°.
View SolutionSum of interior angles of polygon
View SolutionState whether the statements are true (T) or (F) false.
All angles of a trapezium are equal.
View SolutionState whether the statements are True or False.
Sum of two supplementary angles is 180∘.
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true (T) or (F) false.
A quadrilateral can have all four angles as obtuse.
View SolutionState whether the statements are True or False.
Sum of two complementary angles is 180∘.
View Solution
