A particle moves in xy plane such that and where is in m/s and y is in m. It is also known that when . Determine (i) Acceleration of particle (ii) Velocity of particle when .Solution in Gujrati
The correct Answer is:(i) (ii)
Step by step video & image solution for A particle moves in xy plane such that v_(x)=50-16 t and y=100-4t^(2) where v_(x) is in m/s and y is in m. It is also known that x=0 when t=0. Determine (i) Acceleration of particle (ii) Velocity of particle when y=0. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-1)
40 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionA particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View SolutionA particle of mass m moves in pane xy due to the force varying with velocity as F=a(dot(y)-dot(x)j) , where a is a positve constant, i and j are the unit vectors of the x and y axes. At the initial moment t=0 the particle was located at the point x=y=0 and possessed a velocity v_(0) directed along the unit vector j . Find the law of motino x(t), y(t) of the particle, and also the equation of its trajectory.
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View SolutionA particle starts from the origin at t=0s with a velocity of 10.0ˆjm/s and moves in the xy-plane with a constant acceleration of (8ˆi+2ˆj)m/s−2. Then y-coordinate of the particle in 2sec is
View SolutionA particle is moving in the xy plane on a sinusoidal course determined by y = A sin kx, where k and A are constants. The X component of the velocity of the particle is constant and is equal to v_(0) and the particle was at origin at time t = 0 . Find the magnitude of the acceleration of the particle when it is at point having x co ordinate x = (pi)/(2k) .
View SolutionThe instantaneous velocity of a particle moving in xy-plane is →V=(ay)ˆi+(V0)ˆj where y is the instantaneous y co-ordinat of the particle and V0 is the particle starts from origin then its trajectory is
View SolutionA particle moves in x-y plane according to the equations x=4t2+5t+16andy=5t where x, y are in metre and t is in second. The acceleration of the particle is
View SolutionA particle moves along the curve y^(2) = 2x where x = (t^(2))/(2) & y gt 0 . What is the acceleration of the particle at t = 2s ?
View Solutionm द्रव्यमान का एक छोटा कण Xअक्ष से θ कोण पर प्रारम्भिक वेग v0 से x-y तल में चित्रानुसार प्रक्षेपित किया गया है। समय t<v0sinθg पर कण का कोणीय संवेग है:
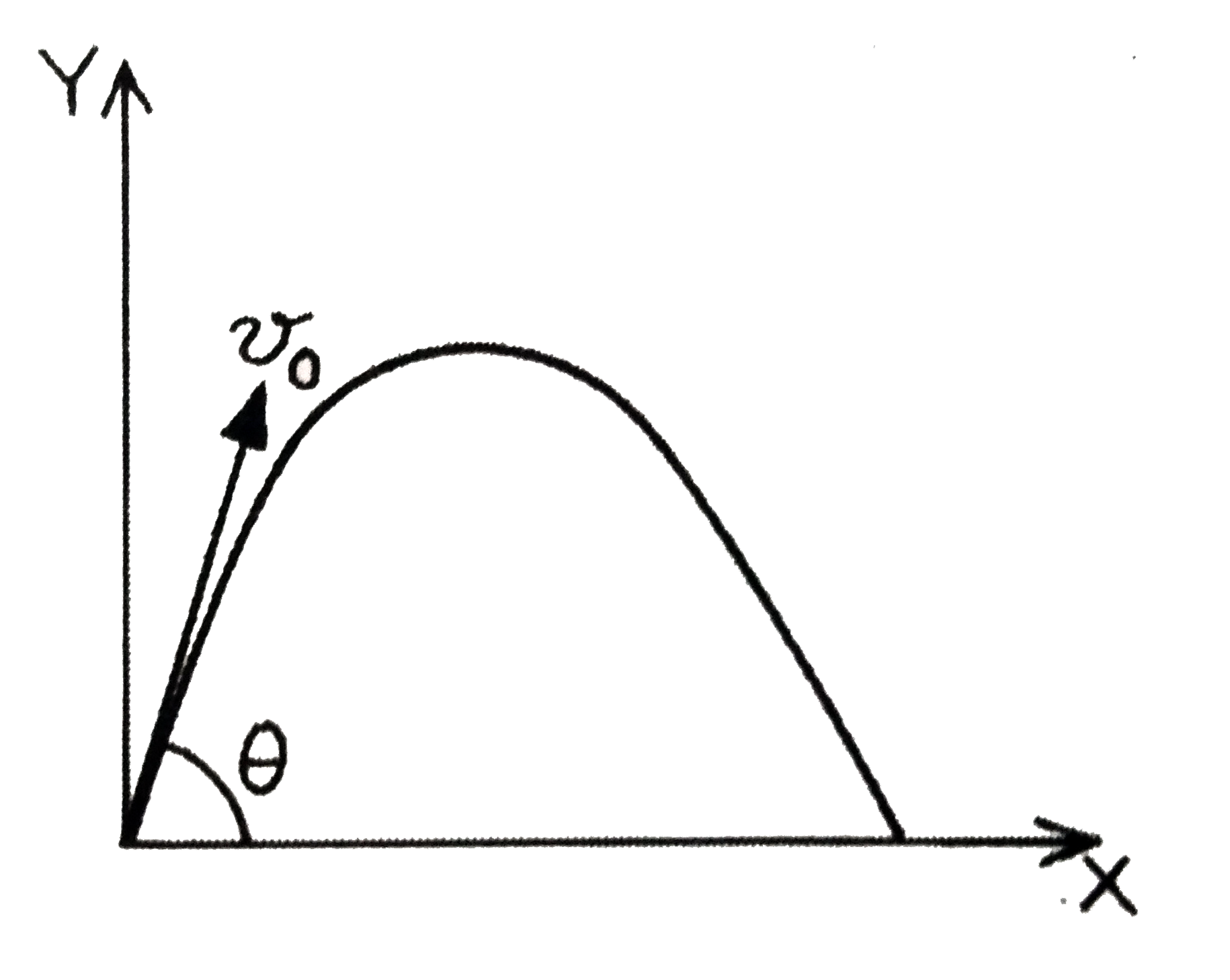
जहां ˆi,ˆj,ˆk,x−,y− तथा z- अक्ष के अनुदिश एकांक सदिश है।
View Solutionसमतल में एकसमान वेग से गतिशील वस्तु के लिए सिद्ध कीजिये की -
x=x0+vxt तथा y=y0+vyt
View Solutionएक कण के वेग के घटक निम्न प्रकार है
vx=(5t) मी./से. vy=(7t) मी./से. कण के त्वरण का मान है
View Solution
