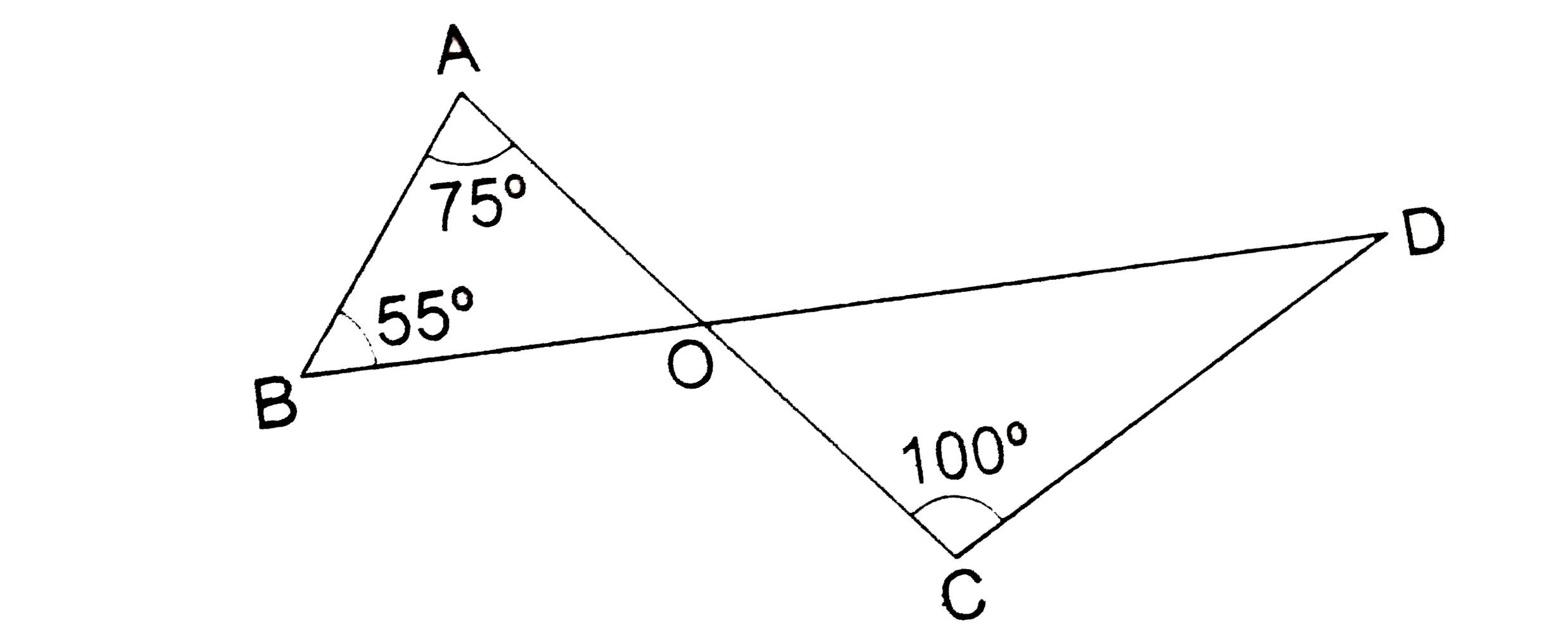
∠ABC=30∘,∠BCO=20∘,∠OCD=20∘,∠ODC=?∘
A
80∘
B
60∘
C
100∘
D
70∘
Video Solution
|
Answer
Step by step video & image solution for angleABC=30^(@),angleBCO=20^(@),angleOCD=20^(@),angleODC=?^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure ∠BAC=30∘,∠ABC=50∘ and ∠CDE=25∘, then ∠AED is equal to
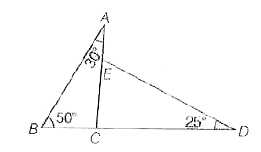 A105∘B115∘C95∘D75∘
A105∘B115∘C95∘D75∘
In the above figure, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DE and ACE is a straight line . I f ∠ABC=30∘ and ∠CDE=20∘, then find ∠BCD.A40∘B50∘C60∘D70∘In the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘ , then ∠AOC is equal to:
 A60∘B80∘C40∘D160∘
A60∘B80∘C40∘D160∘
O is the centre of the circle passing through the points A, B and C such that ∠BAO=30∘,∠BCO=40∘and∠AOC=x∘ . What is the value of x ?
View SolutionIn the given figure, AB∣∣CD. If ∠AOC=30∘ and ∠OAB=100∘ then ∠OCD=?

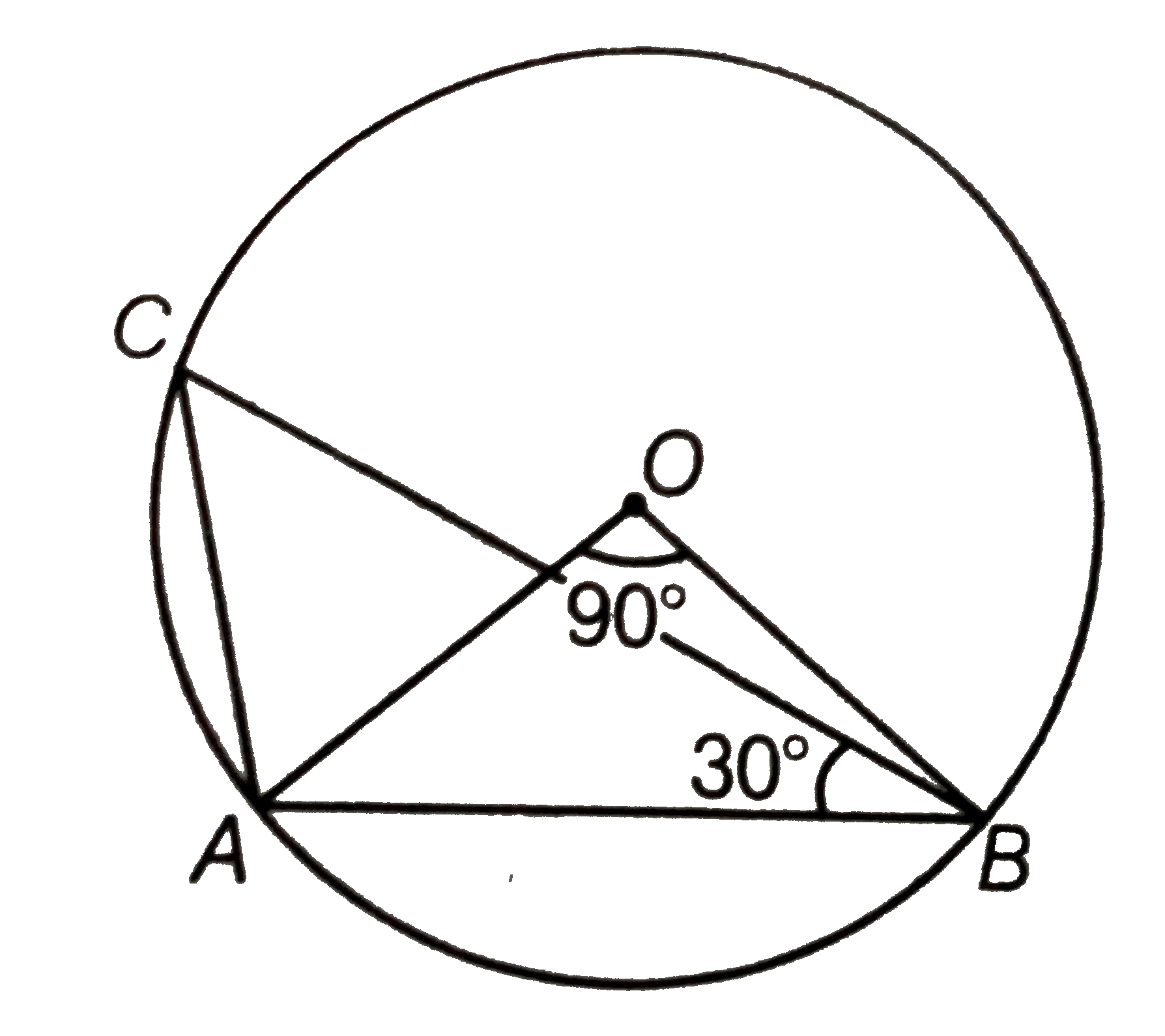
View SolutionIn figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
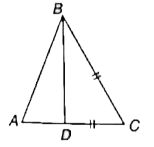
View SolutionIn the triangle ABC,BC=CDand(∠ABC−∠BAC)=30∘. The measure of ∠ABD is :
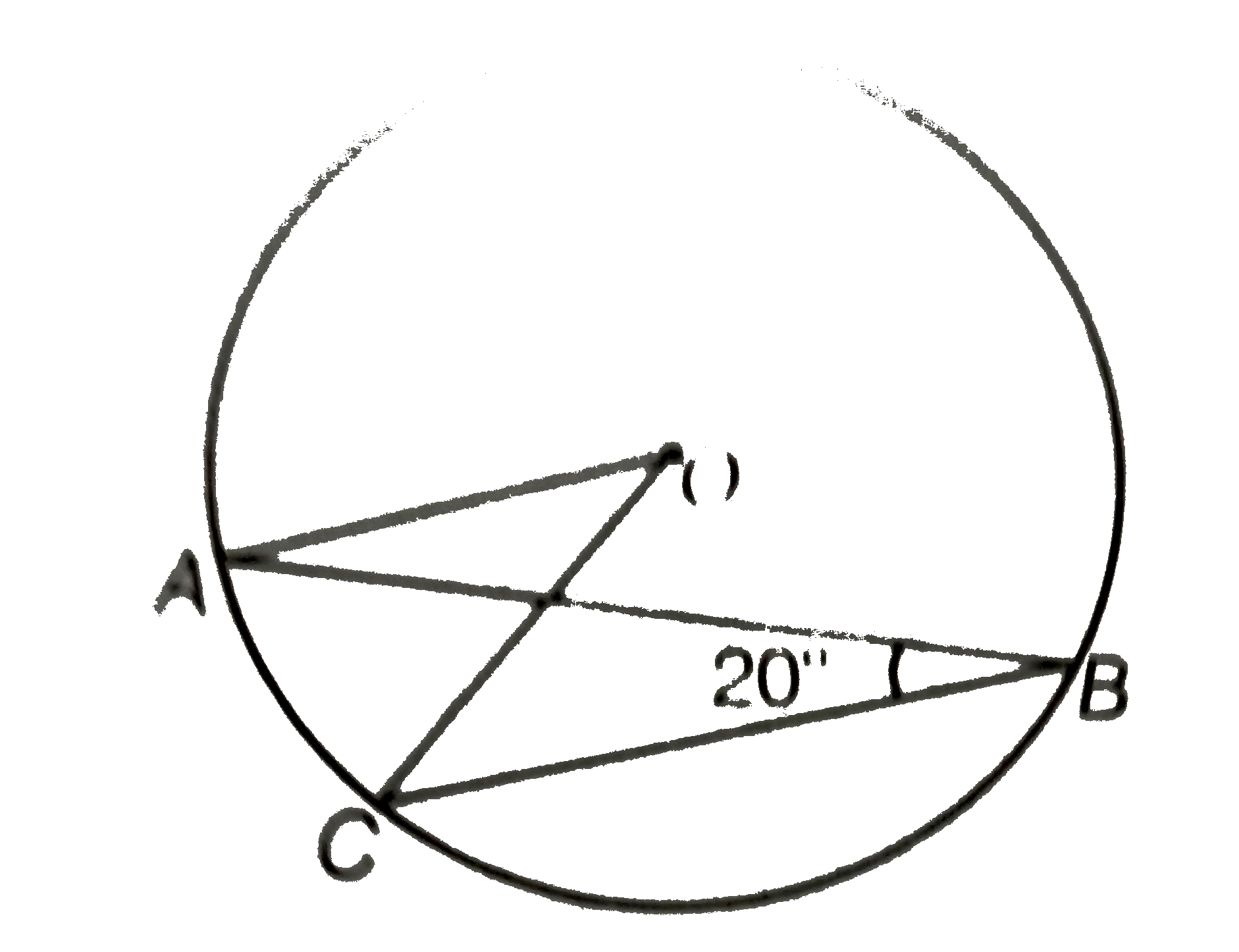
View SolutionIf figure, if∠ABC=20∘,then∠AOC is equal to
View Solution