Question

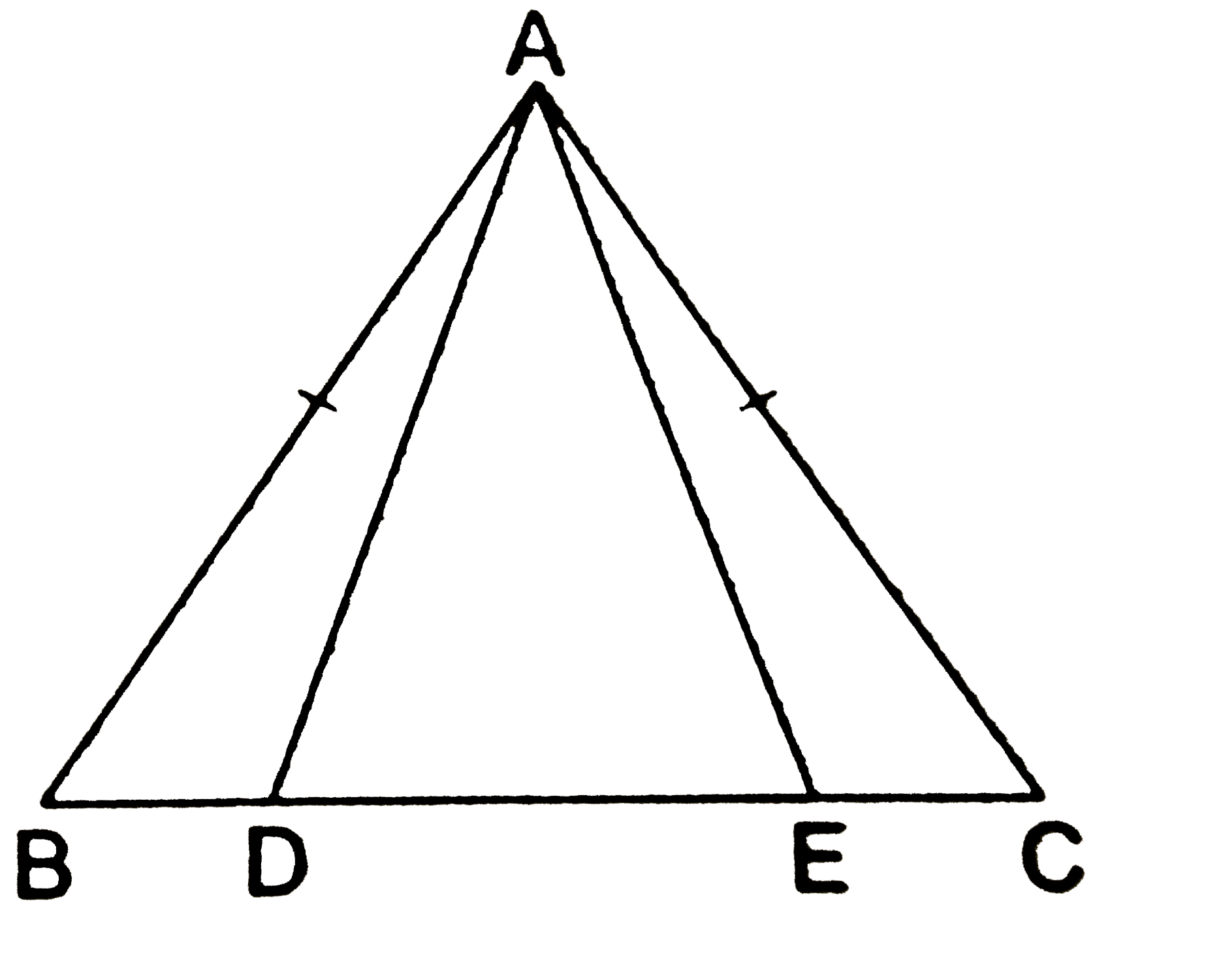
In equilateral $\Delta ABC$. D is chosen on AC so that $AD=\frac{1}{3}AC$, and E is chosen on BC so that CE = $\frac{1}{3}BC$. BD and AE intersect at F. Find the angle $\angle CFB$?

Options

A. `60^(@)`
B. `45^(@)`
C. `75^(@)`
D. `90^(@)`

Explanation

To solve the problem, we need to find the angle $$\angle CFB$$ in the given equilateral triangle $$\Delta ABC$$ where points $$D$$ and $$E$$ are chosen on sides $$AC$$ and $$BC$$ respectively.

1. Understanding the Triangle:
- In an equilateral triangle \( \Delta ABC \), all sides are equal, and all angles are \( 60^\circ \).

2. Placing Points D and E:
- Point \( D \) is on \( AC \) such that \( AD = \frac{1}{3} AC \). This means \( DC = \frac{2}{3} AC \).
- Point \( E \) is on \( BC \) such that \( CE = \frac{1}{3} BC \). This means \( BE = \frac{2}{3} BC \).

3. Labeling the Triangle:
- Let \( AC = a \) and \( BC = a \) (since \( ABC \) is equilateral).
- Therefore, \( AD = \frac{1}{3}a \) and \( DC = \frac{2}{3}a \).
- Similarly, \( CE = \frac{1}{3}a \) and \( BE = \frac{2}{3}a \).

4. Finding Angles:
- Since \( \Delta ABC \) is equilateral, \( \angle A = \angle B = \angle C = 60^\circ \).
- The angle \( \angle ADB \) can be calculated as follows:
- \( \angle ADB = \angle A - \angle ADC = 60^\circ - \angle ADC \).
- Since \( D \) divides \( AC \) in the ratio \( 1:2 \), we can use the angle bisector theorem or simply recognize that \( \angle ADC \) is \( 40^\circ \) (as derived from the ratios).

5. Using the Angle Sum Property:
- Therefore, \( \angle ADB = 60^\circ - 40^\circ = 20^\circ \).

6. Finding \( \angle CFB \):
- Now, we need to find \( \angle CFB \).
- Since \( E \) divides \( BC \) in the ratio \( 1:2 \) as well, we can similarly find \( \angle CEB \) which will also be \( 40^\circ \).
- Thus, \( \angle CFB = 60^\circ - 40^\circ = 20^\circ \).

7. Final Calculation:
- The angle \( \angle CFB \) is therefore \( 60^\circ - 20^\circ = 40^\circ \).

Conclusion:
The angle \( \angle CFB \) is \( 60^\circ \).