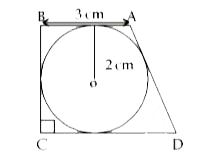
ABCD is a trapezium. An inner circle touches its all sides. Radius of circle is 2 cm and AB = 3 cm. BCD is right angle and AB||CD. Find the area of trapezium.
24 cm
48√2cm
32√2cm
18 cm
Step by step video & image solution for ABCD is a trapezium. An inner circle touches its all sides. Radius of circle is 2 cm and AB = 3 cm. BCD is right angle and AB||CD. Find the area of trapezium. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The parallel sides of a trapezium are 24 cm and 20 cm. The distance between them is 7 cm. Find the radius of a circle whose are is equal to the area of the trapezium.
A9 cmB7 cmC14 cmD28 cmIn a trapezium ABCD, O is the point of intesection of AC and BD, AB||CD and AB=2×CD. If the area of △AOB=84cm2 . Find the area of △COD.
A42cm2B21cm2C25cm2D40cm2In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of these
If circle touches all the sides of a quadrilateral ABCD, if AB = 7 cm, CD = 3 cm, BC = 8.5 cm. Find the length of AD.
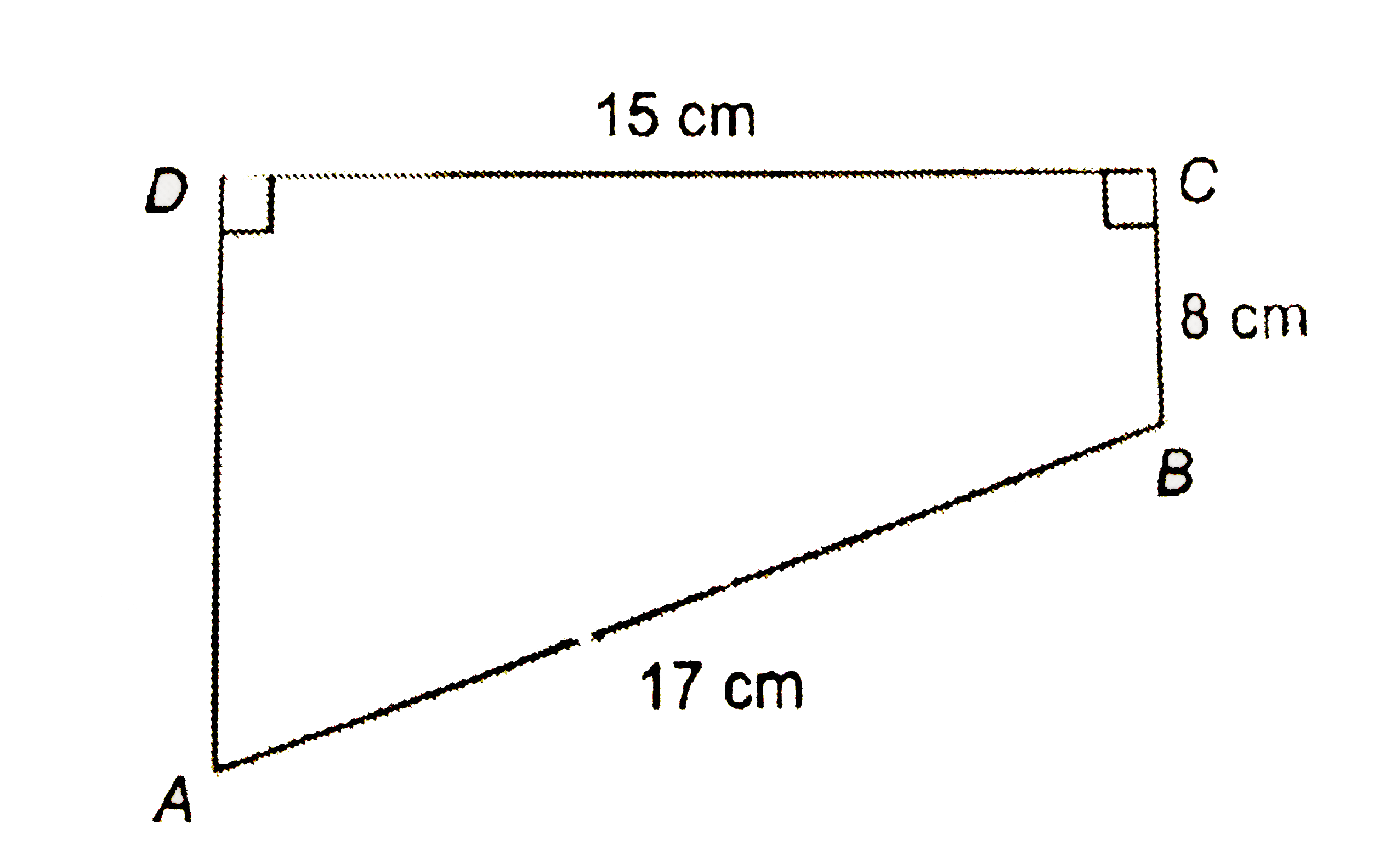
View SolutionIn a trapezium ABCD, AB and DC are parallel sides and ∠ADC=90∘,if AB = 15 cm, CD = 40 cm and diagonal AC = 41 cm. Then the area of the trapezium ABCD is
एक समलंब में AB और DC समांतर किनारे है और ∠ADC=90∘ है । यदि AB = 15 से.मी., CD = 40 से.मी. और विकर्ण AC = 41 से.मी. है, तो उस समलंब ABCD का क्षेत्रफल बताइए ।
View SolutionIn a trapezium ABCD, AB and DC are parallel sides and ∠ADC=90∘ . If AB = 15 cm, CD = 40 cm and diagonal AC = 41 cm. Then the area of the trape- zium ABCD is:
View SolutionIn Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of side AD.
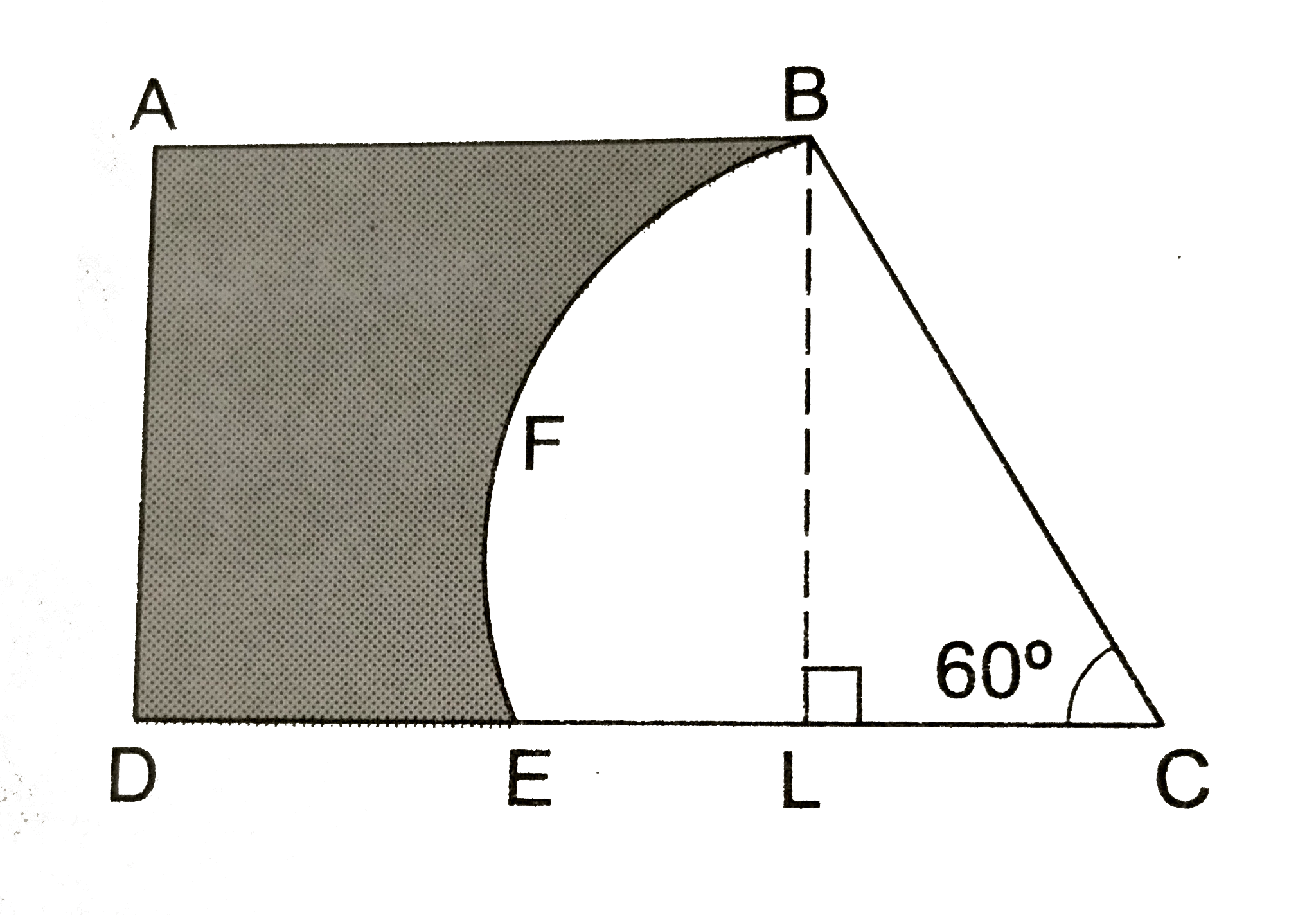
View SolutionIn the given figure, ABCD is a trapezium with AB∣∣CD nad ∠BCD=60∘.If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4cm, then find the area of the shaded region. [Use π=22/7 and √3=1.73]
View Solution