Two particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
The correct Answer is:0.2 sec
To solve the problem, we need to analyze the motion of the two particles under the influence of gravity and determine when their velocity vectors become mutually perpendicular. Here’s a step-by-step solution:
Step 1: Define the initial velocities
Let’s denote the velocities of the two particles:
- Particle 1 has an initial velocity →v1=−1^i m/s (moving in the negative x-direction).
- Particle 2 has an initial velocity →v2=4^i m/s (moving in the positive x-direction).
Step 2: Determine the effect of gravity on the velocities
Since both particles are moving in a uniform gravitational field, the vertical component of their velocities will change over time due to gravity. The vertical component of velocity for both particles after time t will be:
- For Particle 1: v1y=−gt
- For Particle 2: v2y=−gt
Thus, the velocity vectors after time t become:
- →v1(t)=−1^i−gt^j
- →v2(t)=4^i−gt^j
Step 3: Set up the condition for perpendicularity
For the two velocity vectors to be mutually perpendicular, their dot product must be zero:
→v1(t)⋅→v2(t)=0
Calculating the dot product:
(−1^i−gt^j)⋅(4^i−gt^j)=(−1)(4)+(−gt)(−gt)=−4+g2t2
Setting the dot product equal to zero:
−4+g2t2=0
Step 4: Solve for time t
Rearranging the equation gives:
g2t2=4
t2=4g2
t=2g
Step 5: Substitute the value of g
Assuming g=10m/s2:
t=210=0.2s
Conclusion
The time interval after which the velocity vectors of the two particles become mutually perpendicular is t=0.2s.
---
Let’s denote the velocities of the two particles:
- Particle 1 has an initial velocity →v1=−1^i m/s (moving in the negative x-direction).
- Particle 2 has an initial velocity →v2=4^i m/s (moving in the positive x-direction).
Since both particles are moving in a uniform gravitational field, the vertical component of their velocities will change over time due to gravity. The vertical component of velocity for both particles after time t will be:
- For Particle 1: v1y=−gt
- For Particle 2: v2y=−gt
- →v1(t)=−1^i−gt^j
- →v2(t)=4^i−gt^j
For the two velocity vectors to be mutually perpendicular, their dot product must be zero:
→v1(t)⋅→v2(t)=0
(−1^i−gt^j)⋅(4^i−gt^j)=(−1)(4)+(−gt)(−gt)=−4+g2t2
−4+g2t2=0
Rearranging the equation gives:
g2t2=4
t2=4g2
t=2g
Assuming g=10m/s2:
t=210=0.2s
The time interval after which the velocity vectors of the two particles become mutually perpendicular is t=0.2s.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (NEWTONS LAWS OF MOTION)
46 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (FRICTION)
14 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Units, Dimensions & Measurements)
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v1=3m/sandv2=4m/s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
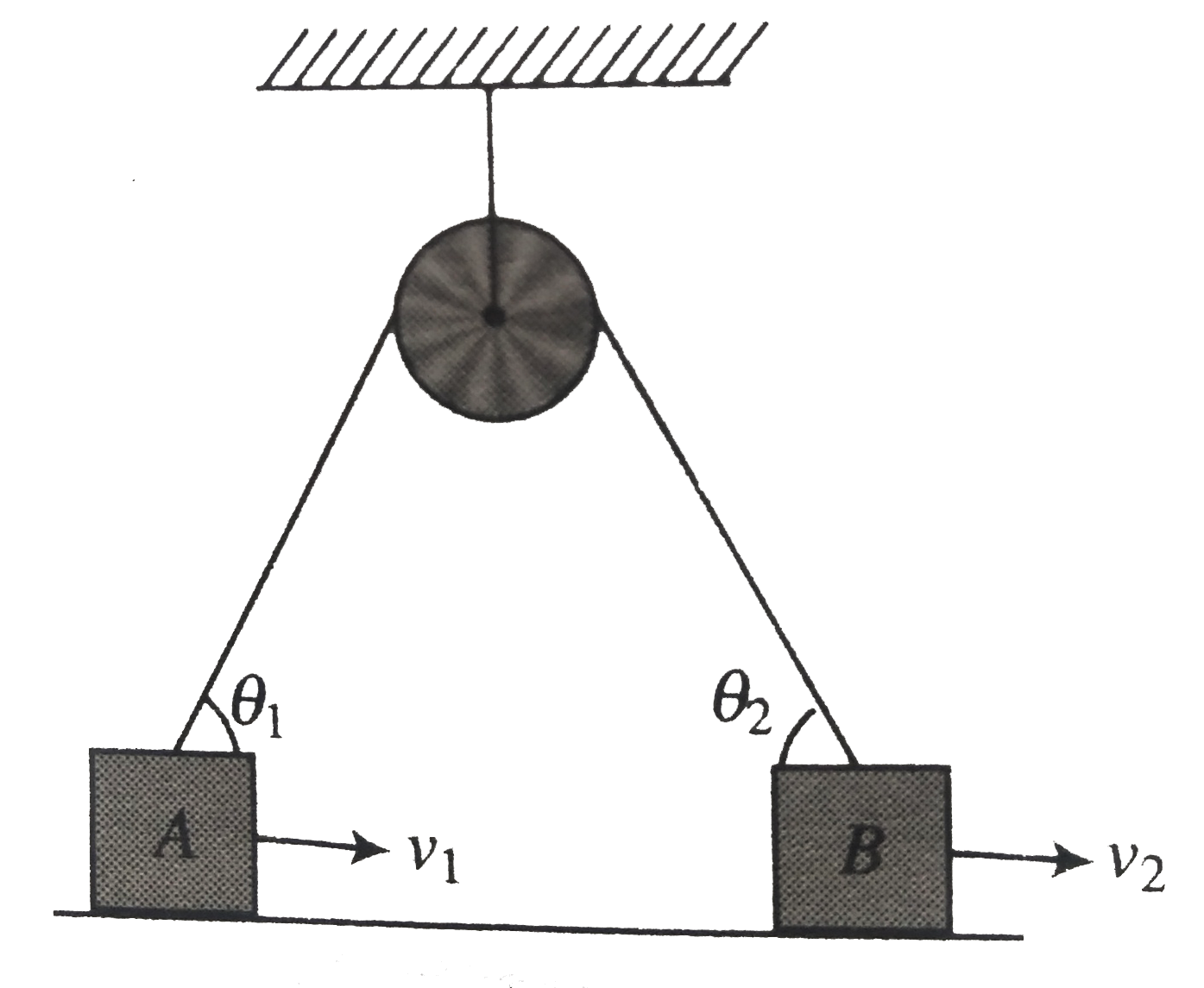
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionTwo particles are projected with speeds u1 and u2 in mutually opposite directions from top of a tower horizontally. Find the time after which their velocity becomes perpendicular to each other.
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionTwo particles are thrown horizontally in opposite directions from the same point from a height h with velocities 4ms−1and3ms−1 . What is the separation between them when their velocities are perpendicular to each other?
View SolutionA train is moving with uniform acceleration. The two ends of the train pass through a point on the track with velocity v1 and v2. With what velocity the middle point of the train would pass through the same point ?
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionTwo particles of masses 3kg and 2kg move due north and due east respectively with the velocities2ms−1and3ms−1. The magnitude and direction of the velocity of centre of mass is
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View Solution
