Calculate energy stored in a capacitor of 5μF when it is charged to a potential of 250 volt.
To calculate the energy stored in a capacitor, we can use the formula:
E=12CV2
where:
- E is the energy stored in the capacitor (in joules),
- C is the capacitance (in farads),
- V is the voltage (in volts).
Step 1: Identify the values given in the problem.
- Capacitance C=5μF=5×10−6F
- Voltage V=250V
Step 2: Substitute the values into the energy formula.
Using the formula E=12CV2:
E=12×(5×10−6F)×(250V)2
Step 3: Calculate V2.
V2=(250)2=62500V2
Step 4: Substitute V2 back into the energy formula.
E=12×(5×10−6)×62500
Step 5: Calculate the energy E.
E=12×(5×10−6)×62500=5×625002×10−6
E=3125002×10−6=156250×10−6=0.15625J
Step 6: Convert the energy into microjoules.
Since 1J=106μJ:
E=0.15625J=156250μJ≈0.156μJ
Final Answer:
The energy stored in the capacitor is approximately 0.156μJ.
---
- E is the energy stored in the capacitor (in joules),
- C is the capacitance (in farads),
- V is the voltage (in volts).
- Capacitance C=5μF=5×10−6F
- Voltage V=250V
Using the formula E=12CV2:
V2=(250)2=62500V2
E=12×(5×10−6)×62500
E=12×(5×10−6)×62500=5×625002×10−6
E=3125002×10−6=156250×10−6=0.15625J
Since 1J=106μJ:
E=0.15625J=156250μJ≈0.156μJ
The energy stored in the capacitor is approximately 0.156μJ.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionMatch the columns

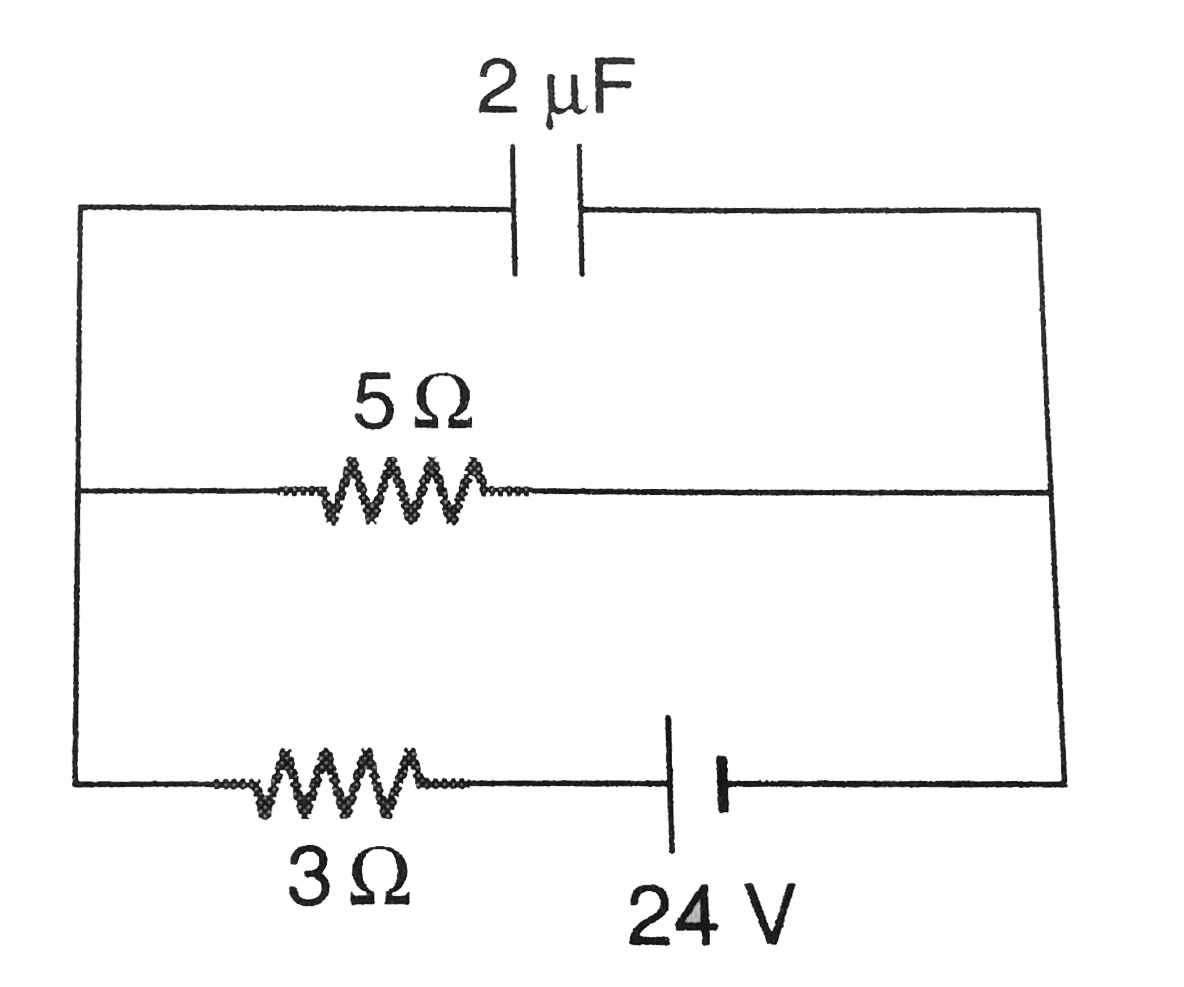
View SolutionFind the charge stored in the capacitor.
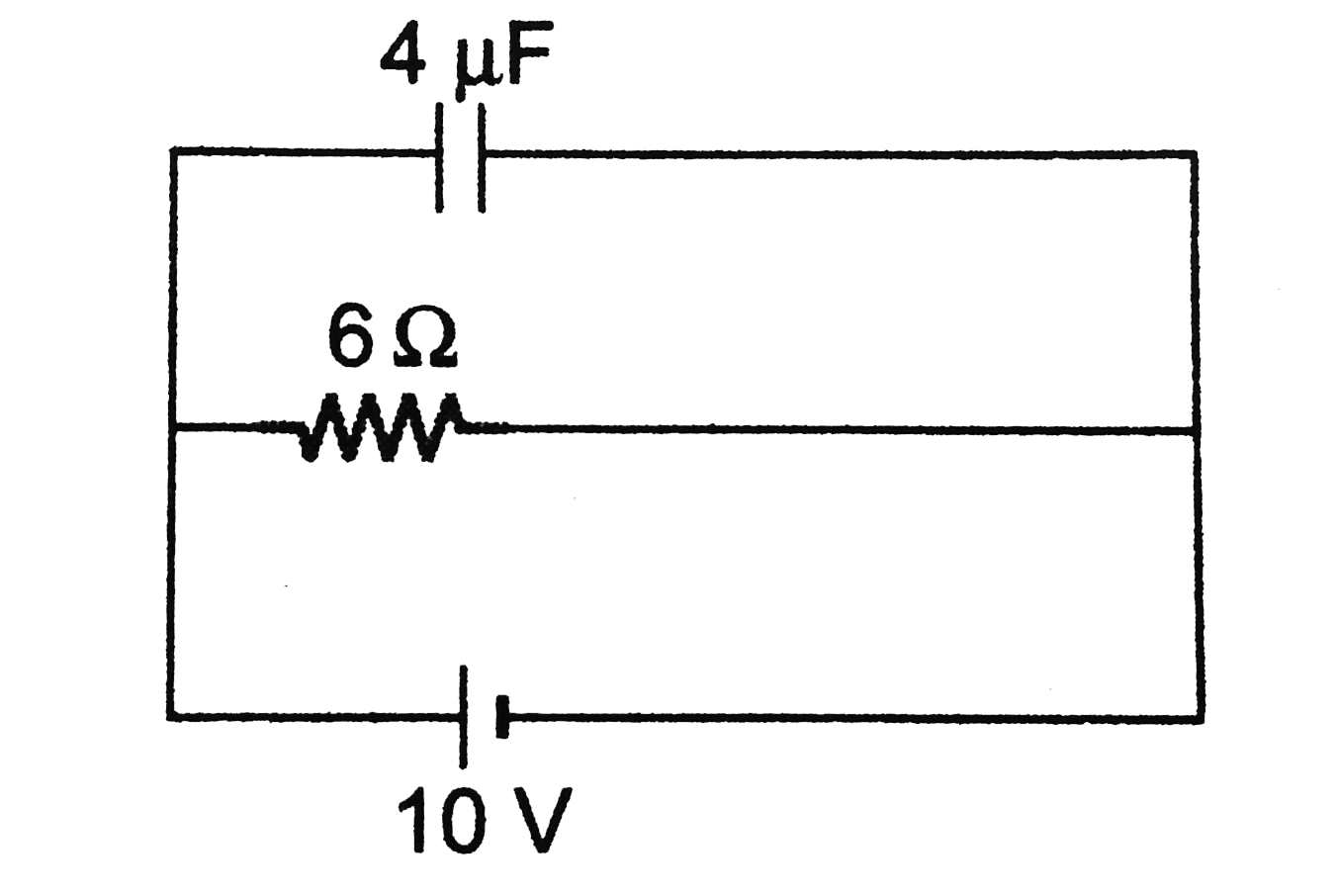
View SolutionFind the charge stored in the capacitor.
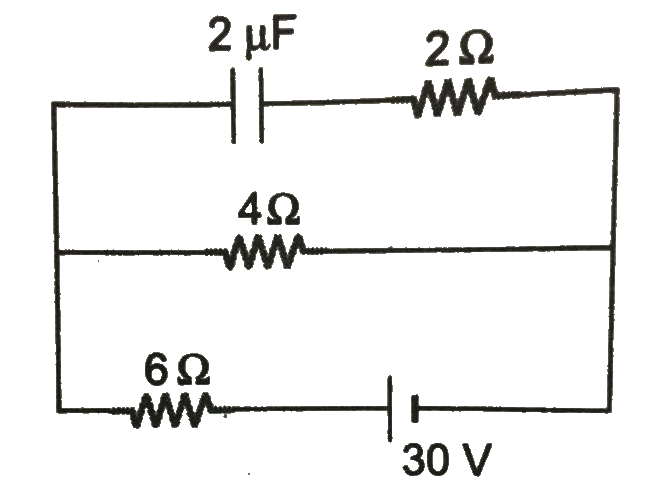
View SolutionFind the charge stored in the capacitor.
View SolutionThe energy stored in a capacitor of capacity C and potential V is given by
View SolutionA capacitor having a capacitance of 100μf is changed to a potential difference of 50V.(a) What is the magnitude of the charge on each plate? (b)The charging battery is disconnected and a dielectric of dielectric constant 2.5 is inserted . Calculate the new potential difference between the plate .
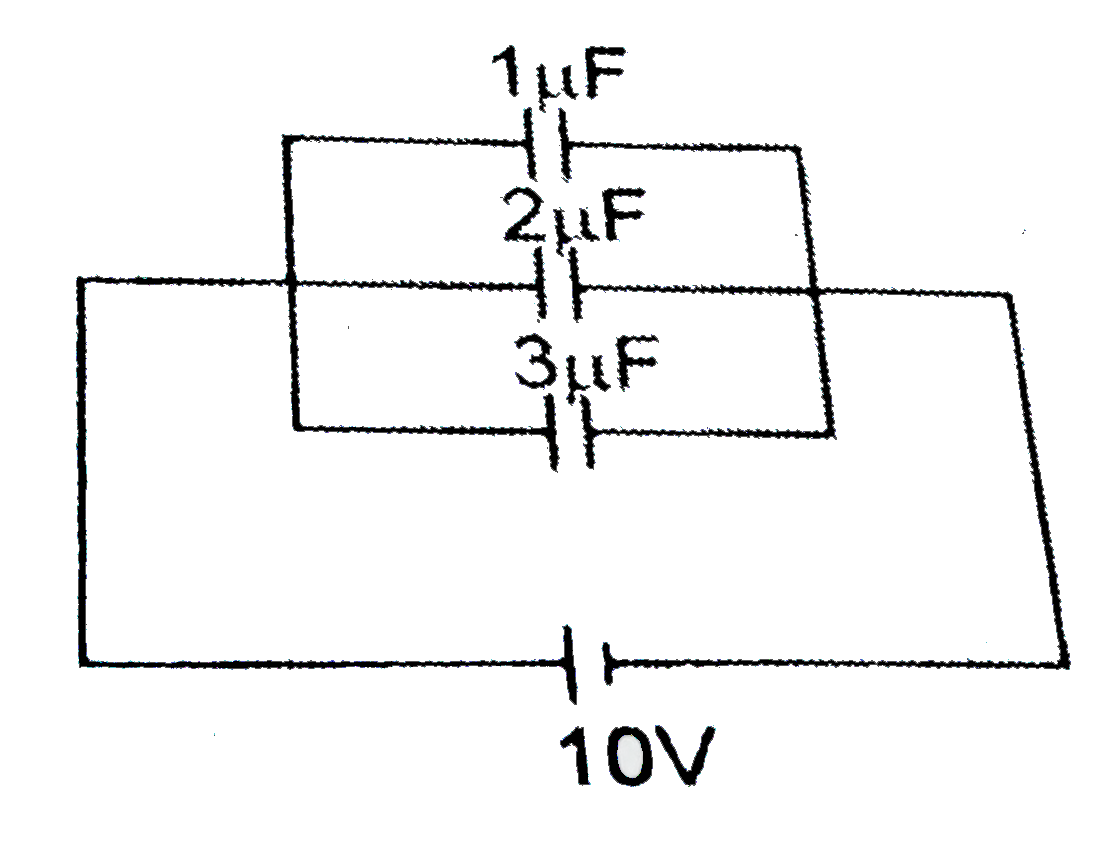
View SolutionThree initially uncharged capacitors are connected to a battery of 10V is parallel combination find out following
(i) charge flow from the battery
(ii) total energy stored in the capacitors
(iii) heat produced in the circuit
(iv) potential energy in the 3μF capacitor.
View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View SolutionA parallel plate capacitor is charged to a potential difference of 50 volts. It is then discharged through a resistance for 2 seconds and its potential drops by 10 volts. Calculate the fraction of energy stored in the capacitance.
View Solution
