Consider a string whose one end is attached to a wall. Then compute the following in both situations given in figure (assume waves crosses the distance in one second)
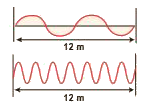
(a) Wavelength, (b) Frequency and (c) Velocity
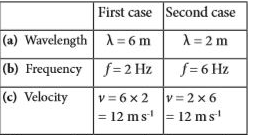
This means that the speed of the wave along a string is a constant. Higher the frequency, shorter the wavelength and vice versa, and their product is velocity which remains the same.
Topper's Solved these Questions
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(I. MULTIPLE CHOICE QUESTIONS)
15 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
- UNITS AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE (ADDITIONAL EXERCISE)
9 Videos
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE - IV. NUMERICAL PROBLEMS
5 Videos
Similar Questions
For a string clamped at both its ends, which of the following wave equation is lare valid for a stationary wave set up in It? (Origin is at one end of string)
View SolutionThe adjacent figure shows a displacement vs distance graph of a wave. If the velocity of the wave is 14ms−1, calculate its
(a) wavelength , (b) frequency and (c) amplitude of the wave
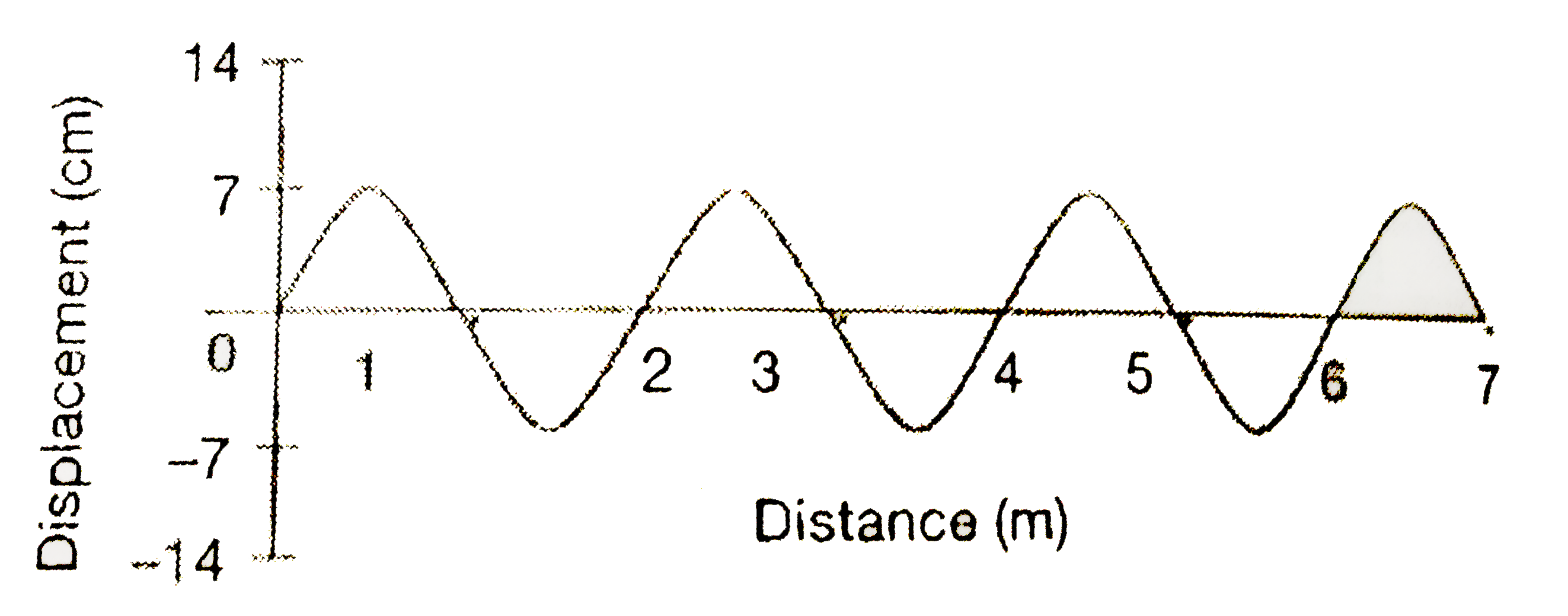
View Solution
Knowledge Check
For a string clamped at both its ends, which of the following wave equation is lare valid for a stationary wave set up in It? (Origin is at one end of string)
Ay=Asinkx.sinωtBy=AcoskxsinωtCy=Asinkx.cosωtDy=AcoskxcosωtThe tension in a stretched string fixed at both ends is changed by 2%, the fundamental frequency is found to get changed by 15Hz.
(a) wavelength of the string of fundamental frequency does not change
(b) velocity of propagation of wave changes by 2%
(c) velocity of propagation of wave changes by 1%
(d) original frequency is 1500HzAc only correctBc and d are correctCa,c and d are correctDb and d are correct
Ivan shakes one end of a rope attached to a wall. This produces a wave motion in the rope. He observes that the first peak of the wave reaches the wall in 5 seconds, and a total of 15 peaks are produced in the vibrating rope in 5 seconds. The length of the rope is 3 meters. What is the wavelength of the wave produced in the rope?
View SolutionA violin string 15.0 cm long and fixed at both ends oscillates in its N = 1 mode. The speed of waves on the string is 280 m/s, and the speed of sound in air is 318 m/s. What are the (a) frequency and (b) wavelength of the emitted sound wave?
View SolutionA series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View SolutionA series of pulses, each of amplitude 0.150m, are sent on a string that is attached to a wall at one end. The pulses are reflected at the wall and travel back along the string without loss of amplitude. When two waves are present on the same string. The net displacement of a given point is the sum of the displacement of the individuals waves at the point. What is the net displacement at point on the spring where two pulses am crossing, (a) if the string is rigidly attached to the post? (b) if the end at which reflection occurs is free is slide up and down ?
View SolutionAn observer rides with a sound source of frequency f and moving with velocity v towards a large vertical wall. Considering the velocity of sound waves as c, find :
(i) The number of waves striking the surface of wall per second
(ii) The wavelength of the reflected wave
(iii) The frequency of reflected wave as observed by observer.
(iv) Beat frequency heard by the observer.
View SolutionAn observer rides with a sound source of frequency f and moving with velocity v towards a large vertical wall. Considering the velocity of sound waves as c, find :
(i) The number of waves striking the surface of wall per second
(ii) The wavelength of the reflected wave
(iii) The frequency of reflected wave as observed by observer.
(iv) Beat frequency heard by the observer.
View Solution
