A heavy particle of mass 0.50 kg is hanging from a string fixed with the roof. Find the force exerted by the string on the particle. Takeg=9.8ms2
 .
.
T is 9.9 N acting vertically upward
T is 4.9 N acting vertically upward
T is 4.9 N acting vertically downward
T is 14.9 N acting vertically upward
The correct Answer is:B
The forces acting on the particle are a. pull of the earth 0.50kg×9.8ms2=4.9N vertically downward
b. pull of the string . T vertically upward.
the particle is at rest with respect to the earth (which we assume to be an inertial frame). Hence, the sum of the forces should be zero. Therefore, T is 4.9 N acting vertically upward.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Worked Out Examples
11 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Short Answer
17 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
A heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block through another string. Find the tensions in the two strings. Take g=10ms2.
View Solution
Knowledge Check
An object of mass 0.75 kg is hanging from a string attached to roof.What will be the force applies by string on the object?
A8.45 NB7.35 NC6,.85 ND9.8 NA body of mass M is being pulled by a string of mass m with a force P applied at one end. The force exerted by the string on the body is
APm(M+m)BPM(M+m)CPm(M+m)DP(M−m)A heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
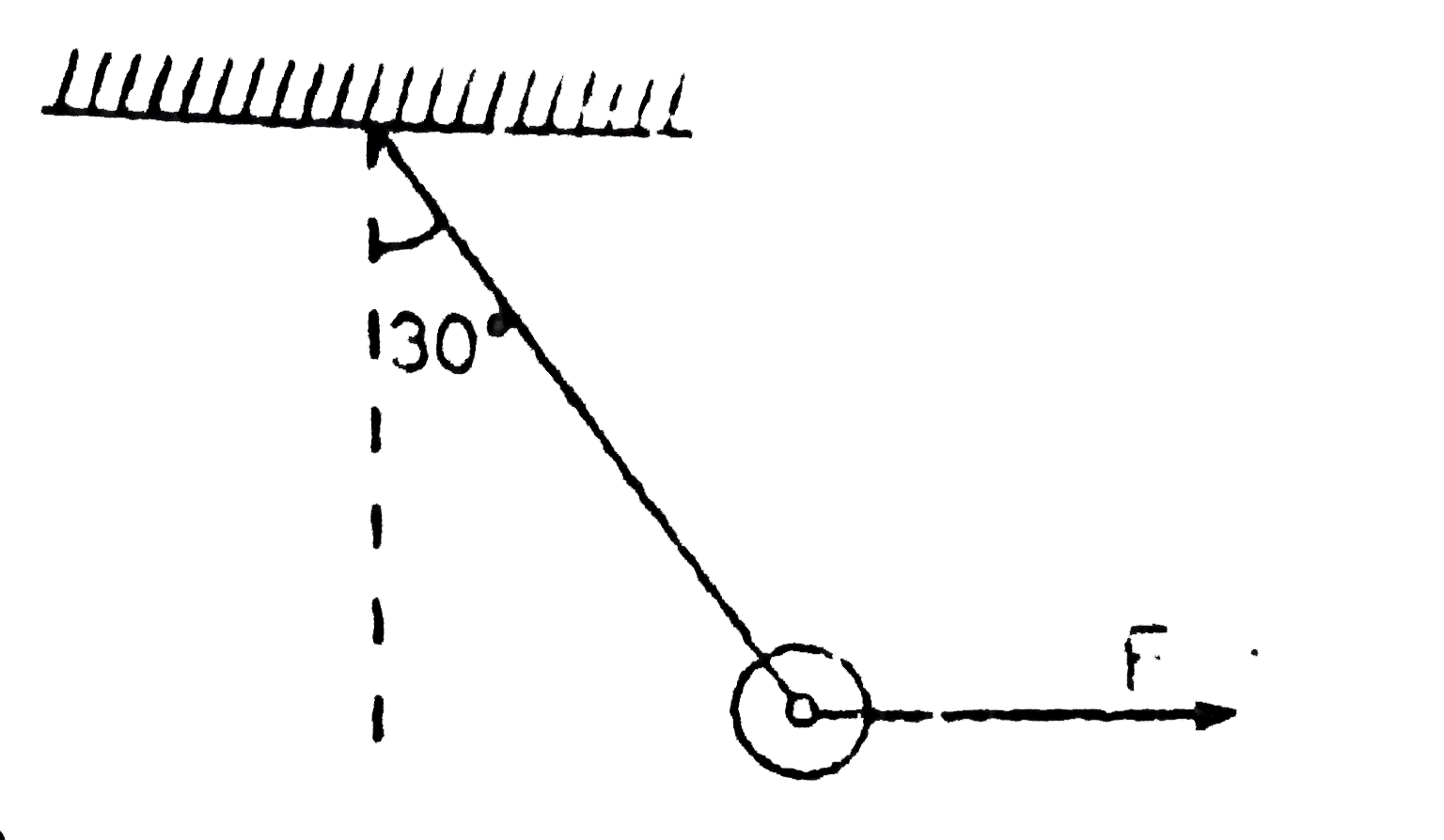 .A10NB10√3NC5ND10√3N
.A10NB10√3NC5ND10√3N
Find the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
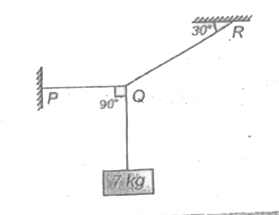
View SolutionA ladder is hanging from ceiling as shownin figure. Three men A, B and C of masses 40 kg, 60 kg, and 50 kg are climbing the ladder. Man A is going up with retardation 2m/s2, C is going up with an acceleration of 1m/s2 and man B is going up with a constantg speed of 0.5 m/s. Find the tension in the string supporting the ledder. [g=9.8m/s2]

View SolutionA 100 cm long wire of mass 40 g supports a mass of 1.6 kg as shown in figure . Find the fundamental frequency of the portion of the string between the wall and the pulley. Take g=10m/s2.

View SolutionA particle of mass m is suspended from a string of length l fixed to the point O. What velocity should be imparted to the particle in its lowermost position so that the string is just able to reach the horizontal diameter of the circle?
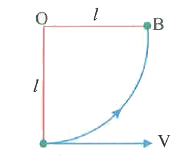
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View Solution
