The parabola $y^{2} = 2 x$ divides the circle $x^{2} + y^{2} = 8$ in two parts. Then, the ratio of the areas of these parts is

A

$\frac{3 π - 2}{10 π + 2}$

B

$\frac{3 π + 2}{9 π - 2}$

C

$\frac{6 π - 3}{11 π - 5}$

D

$\frac{2 π - 9}{9 π + 2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let the area of the smaller part of circle be $A_{1}$ and that of the bigger part be $A_{2}$ . We have to find $\frac{A_{1}}{A_{2}}$ .

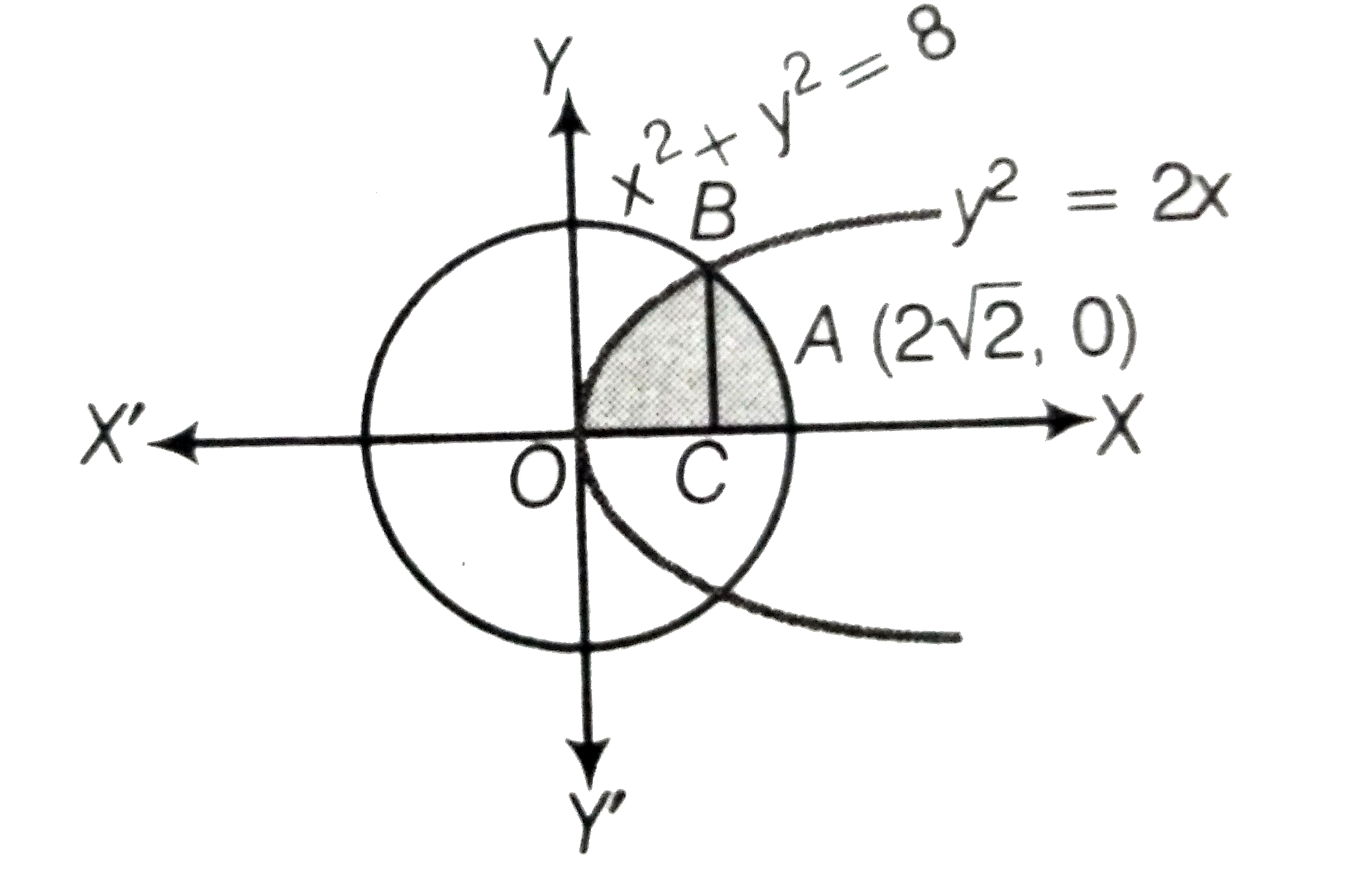
The point B is a point of intersection (lying in the first quadrant) of the given parabola and the circle, whose coordinates can be obtained by solving the two equations $y^{2} = 2 x and x^{2} + y^{2} = 8$ .
$\Rightarrow x^{2} + 2 x = 8$
$\Rightarrow (x - 2) (x + 4) = 0$
$\Rightarrow x = 2, 4$
x = - 4 is not possible as both the points of intersection have the same positive x-coordinate.
Thus, $C \equiv (2, 0)$
Now, $A_{1} = 2 [Area (OBCO) + Area (CBAC)]$
$= 2 [\int_{0}^{2} y_{1} d x + \int_{2}^{2 \sqrt{2}} y_{2} d x]$
where, $y_{1}$ and $y_{2}$ are respectively the values of y from the equations of the parabola and that of the circle.
or $A_{1} = 2 [\int_{0}^{2} \sqrt{2 x} d x + \int_{2}^{2 \sqrt{2}} \sqrt{8 - x^{2}} d x]$
$\Rightarrow A_{1} = 2 {[\sqrt{2} . \frac{2}{3} . x^{3 / 2}]}_{0}^{3 / 2} + 2 {[\frac{x}{2} \sqrt{8 - x^{2}} + \frac{8}{2} {sin}^{- 1} . \frac{x}{2 \sqrt{2}}]}_{2}^{2 \sqrt{2}}$
$= \frac{16}{3} + 2 [2 π + (2 + 4 \times \frac{π}{4})]$
$= (\frac{4}{3} + 2 π)$ sq units
Area of the circle $= π {(2 \sqrt{2})}^{2} = 8 π$ sq units
Hence, $A_{2} = 8 π - A_{1} = 6 π - \frac{4}{3}$
Then, the required ratio $\frac{A_{1}}{A_{2}} = \frac{\frac{4}{3} + 2 π}{6 π - \frac{4}{3}}$
$= \frac{2 + 3 π}{9 π - 2}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The parabola $y^{2} = 4 x + 1$ divides the disc $x^{2} + y^{2} \leq 1$ into two regions with areas $A_{1}$ and $A_{2}$ . Then $| A_{1} - A_{2} |$ equal
A $\frac{1}{3}$
B $\frac{2}{3}$
C $\frac{π}{4}$
D $\frac{π}{3}$
Question 2 - Select One
Let S be the focus of the parabola $y^{2} = 8 x$ and let PQ be the common chord of the circle $x^{2} + y^{2} - 2 x - 4 y = 0$ and the given parabola. The area of the triangle PQS is
A4
B5
C6
D8
Question 3 - Select One
Let S be the focus of the parabola $y^{2} = 8 x$ and let PQ be the common chord of the circle $x^{2} + y^{2} - 2 x - 4 y = 0$ and the given parabola. The area of the triangle PQS is
A4 sq units
B3 sq units
C2 sq units
D8 sq units

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -Exercise 2

Home
Ask Doubt
Profile