Question

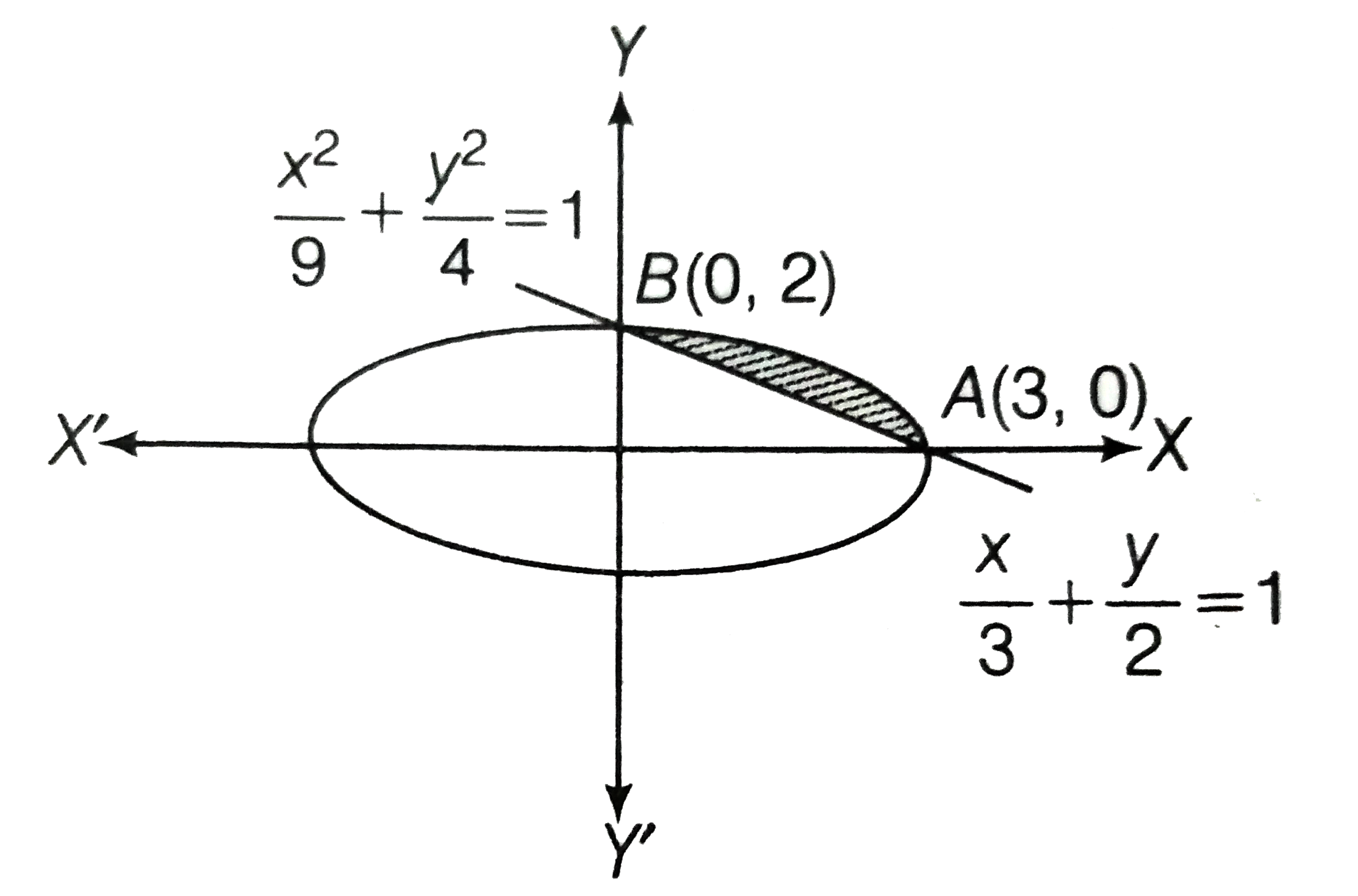
Find the area of the smaller region bounded by the ellipse $\frac{x^2}{9}+\frac{y^2}{4}=1$ and the line $\frac{x}{3}+\frac{y}{2}=1$

Options

A. `3((pi)/(4)-1)` sq unit
B. `3((pi)/(2)-1)` sq unit
C. `4((pi)/(3)-2)` sq unit
D. `3((pi)/(4)-2)` sq unit

Answer

B

Explanation

Given curve is `(x^(2))/(9)+(y^(2))/(4)=1" ... (i)"`
ellipse with centre (0, 0) and given equation of line is
`(x)/(3)+(y)/(2)=1" ... (ii)"`

For finding the points of intersection of ellipse and line, put the value of x from Eq. (ii) in Eq. (i), we get
`(1-(y)/(2))^(2)+(y^(2))/(4)=1rArr(y^(2))/(4)+1-y+(y^(2))/(4)=1`
`rArry^(2)-2y=0rArry=0,2`
When y = 0, then `(x)/(3)+(0)/(2)=1rArrx=3`
When y = 2, then `(x)/(3)+(2)/(2)=1rArrx=0`
So, the points of intersection are A(3, 0) and B(0, 2).
`therefore` Required area `=int_(0)^(3)` [y(ellipse) - y(line)] dx
`=int_(0)^(3)2sqrt(1-(x^(2))/(9))dx-(2)/(3)int_(0)^(3)2(1-(x)/(3))dx`
`=(2)/(3)int_(0)^(3)sqrt(3^(2)-x^(2))dx-(2)/(3)int_(0)^(3)(3-x)dx`
`=(2)/(3)[(x)/(2)sqrt(3^(2)-x^(2))+(9)/(2)sin^(-1).(x)/(3)]_(0)^(3)-(2)/(3)[3x-(x^(2))/(2)]_(0)^(3)" "[because intsqrt(a^(2)-x^(2))dx=(x)/(2)sqrt(a^(2)-x^(2))+(a^(2))/(2)sin^(-1).(x)/(a)]`
`=(2)/(3)[0+(9)/(2)sin^(-1)(1)-0]-(2)/(3)[9-(9)/(2)-0]`
`=3((pi)/(2))-(3)=3((pi)/(2)-1)` sq units