Doubtnut Promotions Sticky

The area bounded by the curves y2=4a(x+a) and y2=4b(b−x), where a,b>0 units

A

83(a+b)√ab sq unit

B

23(a+b)√ab sq unit

C

23(a+b)2√ab sq unit

D

None of the above

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

The two curves are y2=4a(x+a) ... (i)
and y2=−4b(x−b) ... (ii)
Clearly, these two curves represents two parabolas having their vertices at (-a, 0) and (b, 0) respectively as shown in figure.
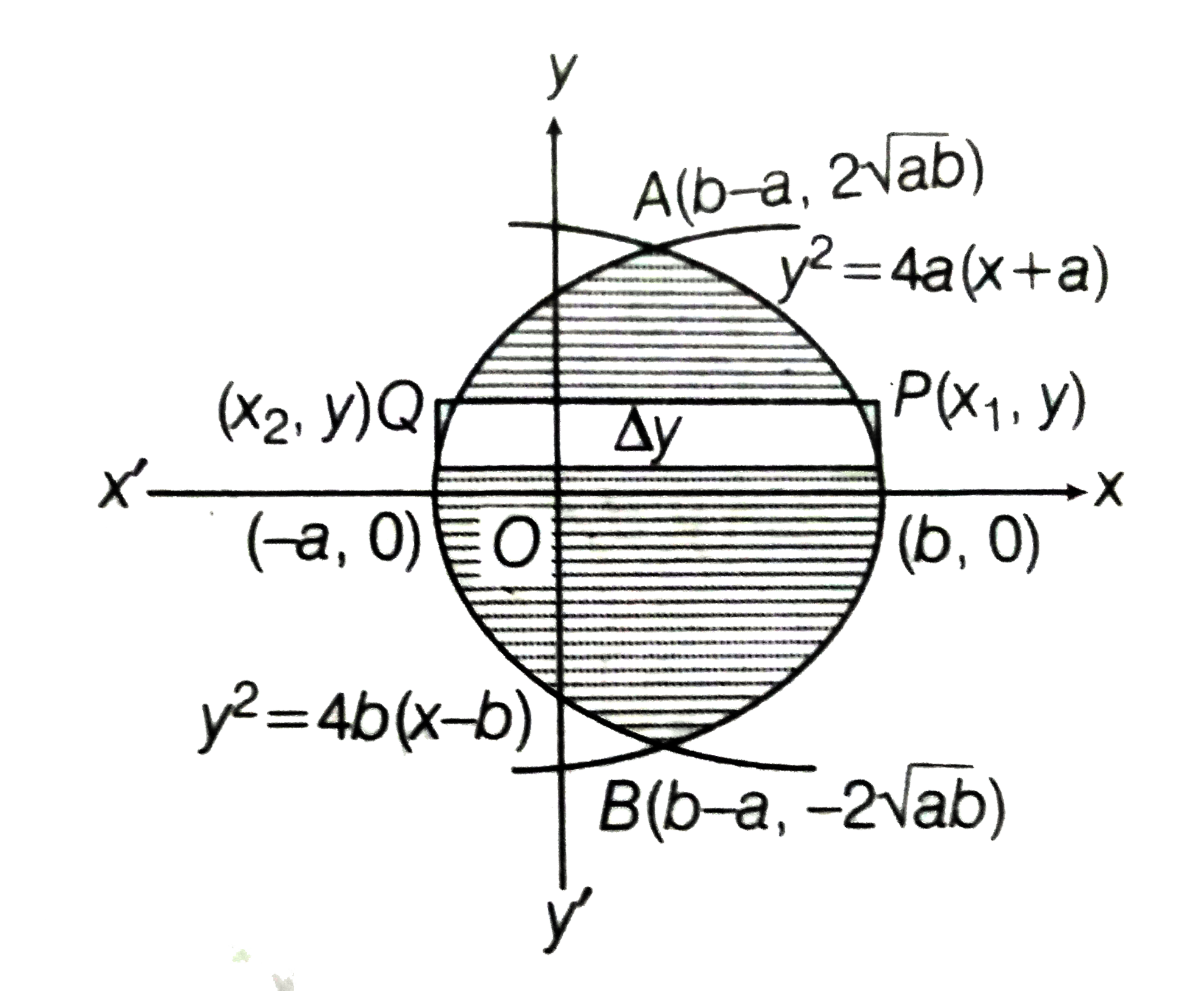
ocr_image
To find teh coordinates of their points of intersection, we solve Eqs. (i) and (ii) together. Solving these equations, we find that the two curves intersect at A(b−a,2√ab) and B(b−a,−2√ab)
∴ Required area =∫2√ab−2√ab(x1−x2)dy
=∫2√ab−2√ab{(b−y24b)−(y24a−a)}dy
⎡⎢⎣∵P(x1,y)andQ(x2,y) lie on (ii) and (i) respectively.∴y2=−4b(x1−b)andy2=4a(x2+a)⎤⎥⎦
=∫2√ab−2√ab{a+b−(a+b4ab)y2}dy
=2∫2√ab0{a+b−(a+b4ab)y2}dy
=2[(a+b)y−(a+b4ab)y33]2√ab0
=2[(a+b)2√ab−(a+b4ab)8ab√ab3]
=2[(a+b)2√ab−23(a+b)√ab]
=83(a+b)√ab sq units

|