If |z−1|+|z+3|≤8, then the range of values of |z−4| is
A
(0,8)
B
[0,9]
C
[1,9]
D
[5,9]
Video Solution
Text Solution
The correct Answer is:C
We have,
|z−1|+|z+3|≤8
⇒|z−(1+0i)|+|z−(−3+0i)|≤8 …………….(i) ltbr> Thus, if P,S and S′ are three points in the Argand plane representing complex numbers, z,1+0i, and −3+0i, then from (i) we obtain.
PS+PS′≤8
⇒ P lies inside and on the ellipse whose two foci are at S(1,0) and S′(−3,0) and major axis =8.
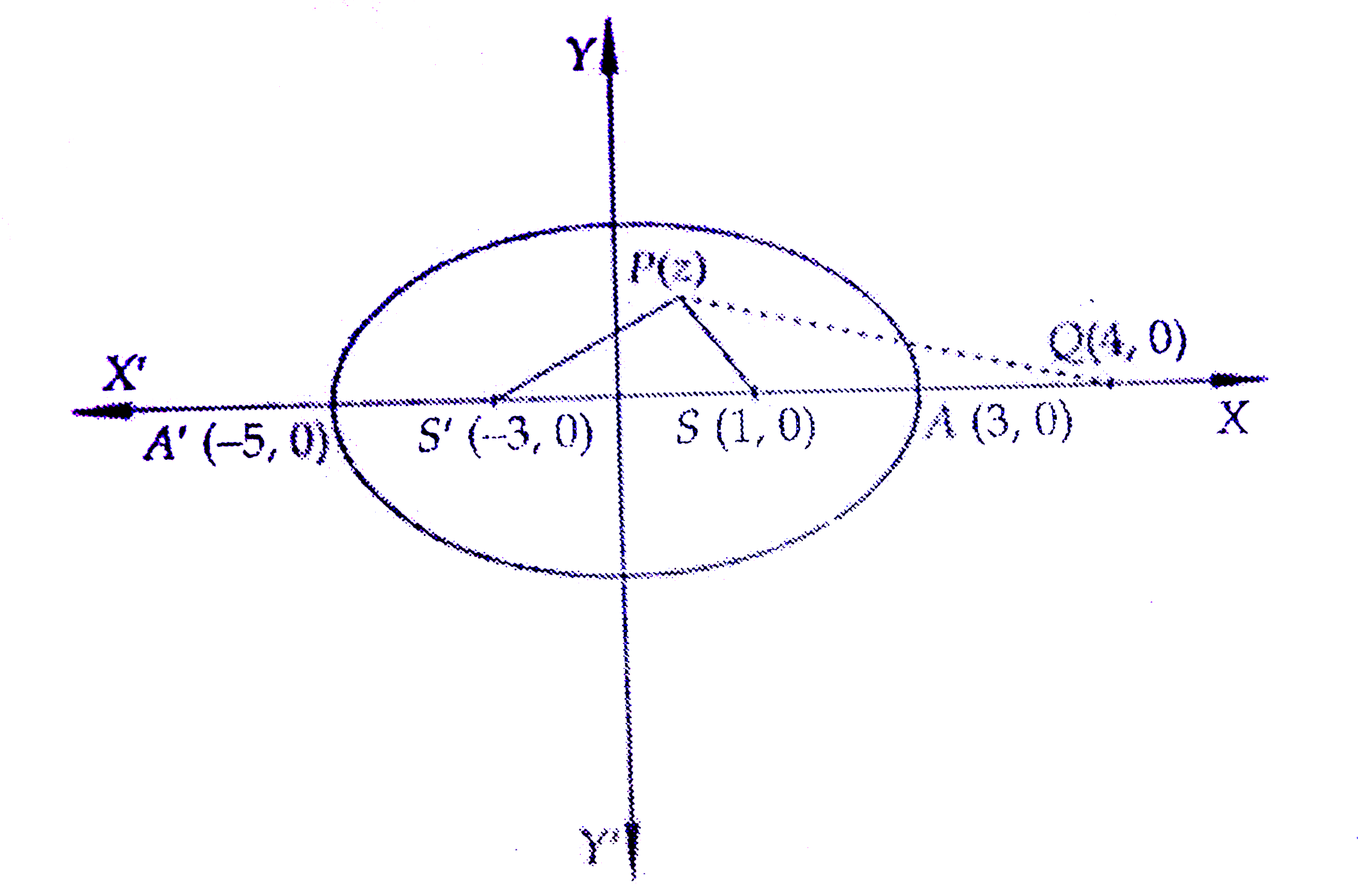
Clearly, PQ =|z−4|
Clearly,PQ is minimum or maximum according as P coincides with A(3,0) and A′(−5,0) respectively.
Thus, PQ=|z−4| varies between AQ=1 and A′Q=9.
Hence, |z−|∈|1,9|.
|
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
If |z1|=|z2|=|z3| and z1+z2+z3=0, then z1,z2,z3 are vertices of
Aa right angled triangleBan equilateral triangleCisosceles triangleDnone of theseIf |z1|=1,|z2|=2,|z3|=3and|9z1z2+4z1z3+z2z3|=12, then the value of |z1+z2+z3| is equal to
A2B3C4D6If |z−2|=min{|z−1|,|z−3|}, where z is a complex number, then
ARe (z)=3/2BRe (z) =5/2CRe (z)∈{32,52}DNone of these
If |z1|=1,|z2|=2,|z3|=3 and |9z1z2+4z1z3+z2z3|=36, then |z1+z2+z3| is equal to :
View SolutionIf z satisfies |z−1|<|z+3| then ω=2z+3−i, (where i=√−1) sqtisfies
View SolutionIf |z1|=1,|z2|=2,|z3|=3 ,then |z1+z2+z3|2+|−z1+z2+z3|2+|z1−z2+z3|2+|z1+z2−z3|2 is equal to
View SolutionThe complex number z satisfying |z−1|=|z−3|=|z−i| is
View SolutionIf |z1|=|z2|=|z3| and z1+z2+z3=0, then z1,z2,z3 are vertices of
View Solution