If A(z1),B(z2)andC(z3) are three points in the argand plane where |z1+z2|=||z1−z2|and|(1−i)z1+iz3|=|z1|+|z3|−z1|, where i=√−1 then
A,B and C lie on a circle with center z2+z32
A,B and C are collinear points.
A,B,C from an equilateral triangle.
A,B,C form an obtuse angle triangle.
The correct Answer is:A
We have,
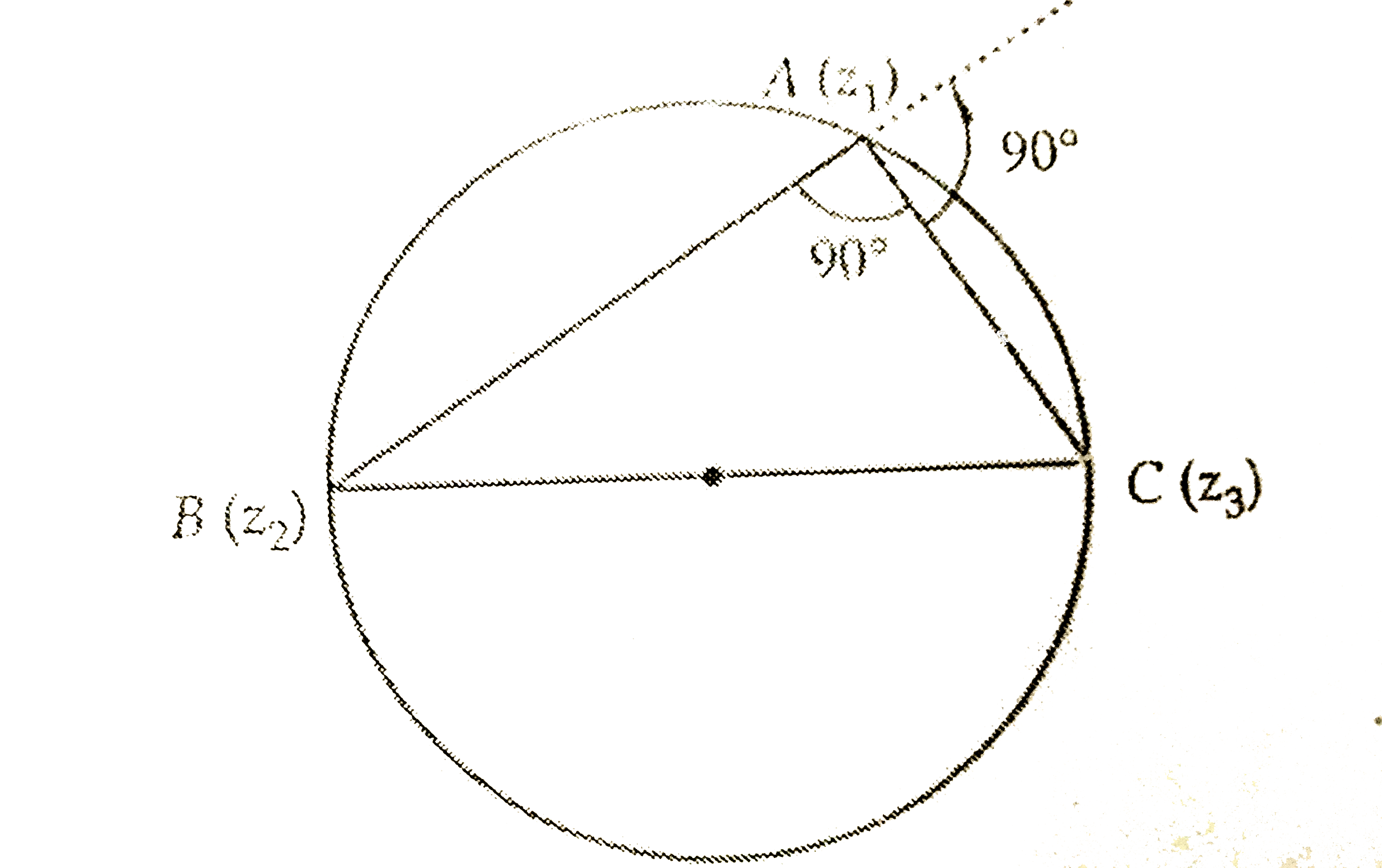
|z1+z2|=||z1|−|z2∣∣<⇒Arg(z1z2)=±π
and |(1−i)z1+iz3|=|z1|+|z3−z1|
<⇒|z1+i(z3−z1)|=|z1|+|z3−z1|
⇒arg(z1z3−z1=π2[∴|z1+iz2|=|z1|+|z2|<⇒arg(z1z2)=π2]
Thus, A lies on the circle with BC as diameter i.e., z2+z32 as center. Hence, option (a) is correct.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Section II - Assertion Reason Type
15 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Exercise
131 Videos
- COMPLEX NUMBERS BOOK - OBJECTIVE RD SHARMACHAPTER - COMPLEX NUMBERS EXERCISE - Chapter Test
59 Videos
- CIRCLESBOOK - OBJECTIVE RD SHARMACHAPTER - CIRCLESEXERCISE - Chapter Test
55 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
Similar Questions
Knowledge Check
If A(z1) and B(z2) are two fixed points in the Argand plane the locus of point P(z) satisfying |z−z1|+|z−z2|=|z1−z2|, is
Aline passing through A and BBline segment joining A and BCan ellipseDa circleIf z1,z2andz3 are the vertices of a triangle in the argand plane such that |z1−z2|=|z1−z3|, then ∣∣∣arg(2z1−z2−z3z3−z2)∣∣∣ is
Aπ3B0Cπ2Dπ6On the Argand plane ,let z1=−2+3z,z2=−2−3z and |z|=1. Then
Az1 moves on circle with centre at (−2,0) and radius 3Bz1 and z2 describle the same locusCz1 and z2 move on differenet circlesDz1−z2 moves on a circle concetric with |z|=1
If P(z) is a variable point and A(z1)andB(z2) are the two fixed points in the argand plane |z−z1|+|z−z2|=|z1−z2|, then find locus of z?
View SolutionLet A(z1),B(z2)andC(z3) be the vertices of an equilateral triangle in the Argand plane such that |z1|=|z2|=|z3|. Then (A) z2+z32z1−z2−z3is purely real (B) z2−z32z1−z2−z3 is purely imaginary (C) ∣∣∣arg(z1z2)∣∣∣=2arg(z3−z2z1−z2)∣∣∣ (D) none of these
View SolutionIf P(z) is a variable point and A(z1)andB(z2) are the two fixed points in the argand plane |z−z1|−|z−z2|=|z1−z2|, then find locus of z?
View SolutionThe points A(z1),B(z2)andC(z3) form an isosceles triangle in the Argand plane right angled at B, then z1−z2z3−z2 can be (A) 1 (B) -1 (C) −i (D) none of these
View SolutionIf P(z) is a variable point and A(z1)andB(z2) are the two fixed points in the argand plane |z−z1|2+|z−z2|2=|z1−z2|2, then find locus of z.
View Solution
