A ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.
The correct Answer is:For r<R,E=kqr2=ρ0r3ε0[1−3r4R],
For r>R, E=(kq)/(r^(2))=(rho_(0)R^(3))/(12 epsilon_(0)r^(2))
To solve the problem step-by-step, we will break it down into two parts as outlined in the question: (a) finding the electric field strength both inside and outside the ball, and (b) finding the maximum intensity and the corresponding distance.
Part (a): Electric Field Strength Inside and Outside the Ball
1. Understanding Charge Density:
The volume charge density is given by:
ρ(r)=ρ0(1−rR)
where ρ0 is a constant, r is the distance from the center, and R is the radius of the ball.
2. Electric Field Outside the Ball:
For points outside the ball (i.e., r>R), we can use Gauss's Law:
ΦE=Qinsideϵ0
Here, ΦE=E⋅A where A=4πr2 is the surface area of the Gaussian surface.
To find Qinside, we integrate the charge density over the volume of the ball:
Qinside=∫R0ρ(r)dV=∫R0ρ0(1−rR)4πr2dr
Evaluating this integral:
Qinside=4πρ0∫R0(r2−r3R)dr=4πρ0(r33−r44R)R0
=4πρ0(R33−R44R)=4πρ0(R33−R34)=4πρ0(4R3−3R312)=πρ0R33
Now substituting Qinside into Gauss's Law:
E⋅4πr2=πρ0R33ϵ0
E=ρ0R312ϵ0r2for r>R
3. Electric Field Inside the Ball:
For points inside the ball (i.e., r<R), we again use Gauss's Law:
Qinside=∫r0ρ(r)dV=∫r0ρ0(1−r′R)4π(r′)2dr′
Evaluating this integral:
Qinside=4πρ0∫r0((r′)2−(r′)3R)dr′=4πρ0((r′)33−(r′)44R)r0
=4πρ0(r33−r44R)
Now substituting Qinside into Gauss's Law:
E⋅4πr2=4πρ0(r33−r44R)ϵ0
E=ρ03ϵ0r(1−3r4R)for r<R
Part (b): Finding Maximum Intensity Emax and Corresponding Distance rm
1. Finding Maximum Electric Field:
To find the maximum electric field, we differentiate the expression for E inside the ball with respect to r and set it to zero:
dEdr=0
From the expression:
E=ρ03ϵ0r(1−3r4R)
Differentiate:
dEdr=ρ03ϵ0(1−3r4R)+ρ03ϵ0r(−34R)=0
Setting the derivative to zero gives:
1−3r4R−3r4R=0⟹1−6r4R=0⟹rm=2R3
2. Calculating Maximum Electric Field:
Substitute rm back into the expression for E:
Emax=ρ03ϵ0(2R3)⎛⎝1−3⋅2R34R⎞⎠
Simplifying:
=ρ03ϵ0(2R3)(1−1.54)=ρ03ϵ0(2R3)(58)=5ρ0R72ϵ0
Summary of Results
- Electric Field Strength:
- Inside the ball (r<R):
E=ρ03ϵ0r(1−3r4R)
- Outside the ball (r>R):
E=ρ0R312ϵ0r2
- Maximum Electric Field Emax:
Emax=5ρ0R72ϵ0
- Corresponding distance rm:
rm=2R3
The volume charge density is given by:
ρ(r)=ρ0(1−rR)
where ρ0 is a constant, r is the distance from the center, and R is the radius of the ball.
For points outside the ball (i.e., r>R), we can use Gauss's Law:
ΦE=Qinsideϵ0
Here, ΦE=E⋅A where A=4πr2 is the surface area of the Gaussian surface.
Qinside=∫R0ρ(r)dV=∫R0ρ0(1−rR)4πr2dr
Evaluating this integral:
Qinside=4πρ0∫R0(r2−r3R)dr=4πρ0(r33−r44R)R0
=4πρ0(R33−R44R)=4πρ0(R33−R34)=4πρ0(4R3−3R312)=πρ0R33
E⋅4πr2=πρ0R33ϵ0
E=ρ0R312ϵ0r2for r>R
For points inside the ball (i.e., r<R), we again use Gauss's Law:
Qinside=∫r0ρ(r)dV=∫r0ρ0(1−r′R)4π(r′)2dr′
Evaluating this integral:
Qinside=4πρ0∫r0((r′)2−(r′)3R)dr′=4πρ0((r′)33−(r′)44R)r0
=4πρ0(r33−r44R)
E⋅4πr2=4πρ0(r33−r44R)ϵ0
E=ρ03ϵ0r(1−3r4R)for r<R
To find the maximum electric field, we differentiate the expression for E inside the ball with respect to r and set it to zero:
dEdr=0
From the expression:
E=ρ03ϵ0r(1−3r4R)
Differentiate:
dEdr=ρ03ϵ0(1−3r4R)+ρ03ϵ0r(−34R)=0
Setting the derivative to zero gives:
1−3r4R−3r4R=0⟹1−6r4R=0⟹rm=2R3
Substitute rm back into the expression for E:
Emax=ρ03ϵ0(2R3)⎛⎝1−3⋅2R34R⎞⎠
Simplifying:
=ρ03ϵ0(2R3)(1−1.54)=ρ03ϵ0(2R3)(58)=5ρ0R72ϵ0
- Electric Field Strength:
- Inside the ball (r<R):
E=ρ03ϵ0r(1−3r4R)
- Outside the ball (r>R):
E=ρ0R312ϵ0r2
Emax=5ρ0R72ϵ0
- Corresponding distance rm:
rm=2R3
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Single Correct
Explore 47 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct
Explore 8 Videos
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Subjective Type
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
Similar Questions
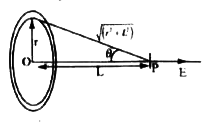
A thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L>>r Find maximum field strength and the corresponding distance L.
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
the maximum electric field intensity is
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
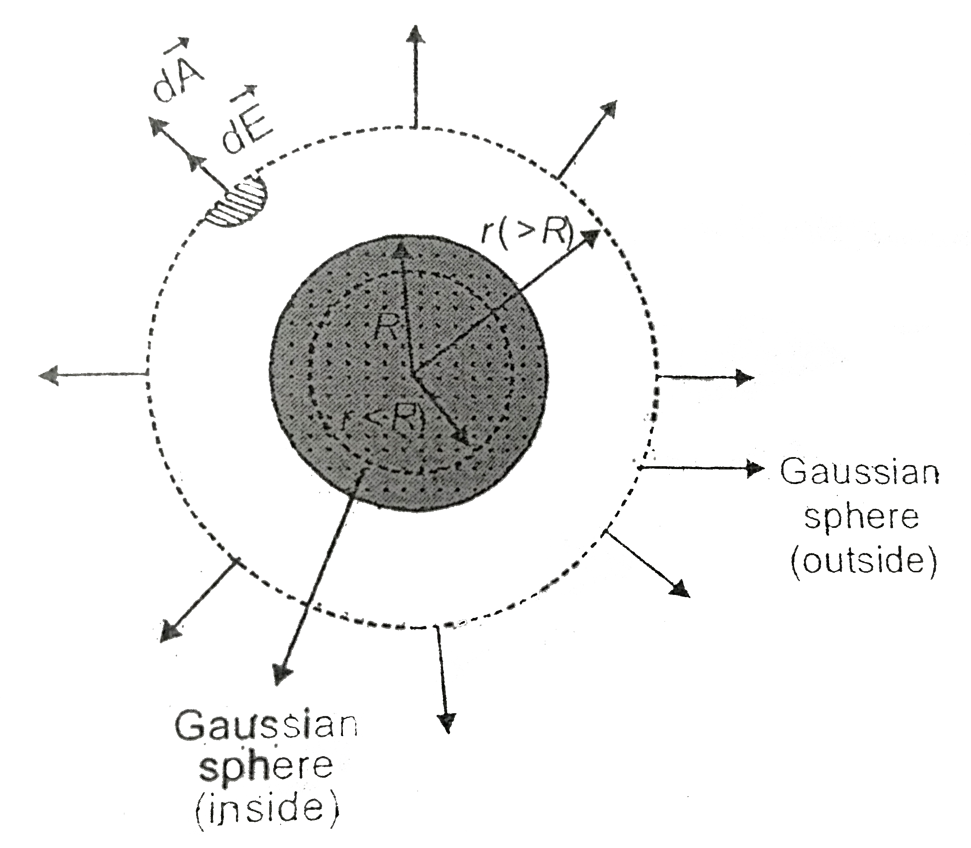
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]

View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of electric field as a function of the distance r inside the sphere is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume charge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), whereρ0 is constant. Assume epsilon as theh permittivity of space.
The magnitude of the electric field as a functiion of the distance r outside the balll is given by
View SolutionA sphere of charges of radius R carries a positive charge whose volume chasrge density depends only on the distance r from the ball's centre as ρ=ρ0(1−rR), where ρ0 is constant. Assume epsilon as theh permittivity of space.
The value of distance rm at which electric field intensity is maximum is given by
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View Solution
