A conducting frame abcd is kept in a vertical plane. A conducting rod of of mass m and length l can slide smoothly on it remaining always horizontal. The resistance of the loop is negligible and inductance is constant having value L. The rod is left from rest and allowed to fall under gravity and inductor has no initial current. A magnetic field of constant magnitude Bis present throughout the loop pointing inwards. Determine

(a) position of the rod as a function of time assuming initial position of the rod to be x=0 and vertically downward as the positive x-axis.
(b) the maximum current in the circuit.
(c) maximum velocity of the rod
The correct Answer is:B
a. Suppose v be the velocity of rod ef whenit has fallen a distane d. Then,
Vfe=Vcb or Bvl=(di/dt)
or (Bdx/dt)l=L(di/dt) or Bl(dx)=L(dt)
Integrating we get Li=Blx
or i=(BlL)x………….(i)
Now magnetic force opposite to displacement x will be
F=Fm=ilB=(B2l2L)x
A constant downward force is mg.

so, this is similar situation like spring clock system in vertical position. in wich a force F=kx acts upwards and a constant force mg acts downwards.
hence, the wire will execute SHM, where
k=B2l2L
Ampltude will be at Fm=mg
or (B2l2L)A=mg⇒A=mgLB2l2
At t=0, rod is in its extreme position.
Therefore if we write the equation from mean position we will write
X=−Acosωt
But x=X+A=A−Acosωt=A(1−cosωt)
where, ω=√km=√B2l2mL
b. From Eqn i
imax=(BlL)xmax
Here xmax=2A=2mgLB2l2
∴imax=(BlL)(2mgLB2l2)=2mgBl
c. Maximum velocity
v0=ωA=(√B2l2mL)(mgLB2l2)=g√mLB2l2=g√mLBl
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - SUBJECTIVE TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
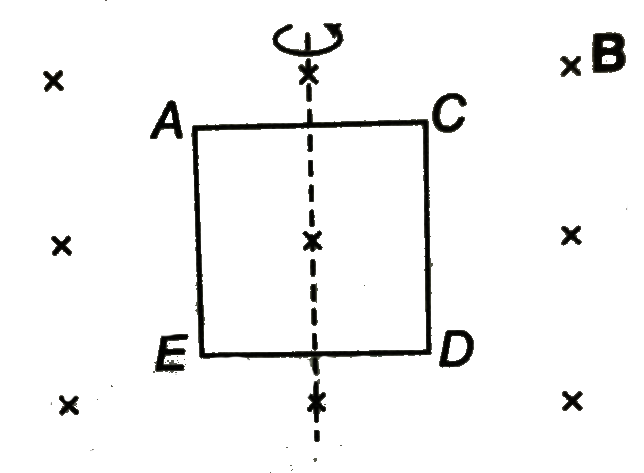
A square loop ACDE of area 20cm2 resistance 5Ω is rotate in as magnetic field B=2T through 180∘ (a) in 0.01s and (b) in 0.02s
Find the magnitudes of averasge values of e i and △q in both the cases.
View SolutionThe magnetic flux linked with a vector area →A in a uniform magnetic field →B is
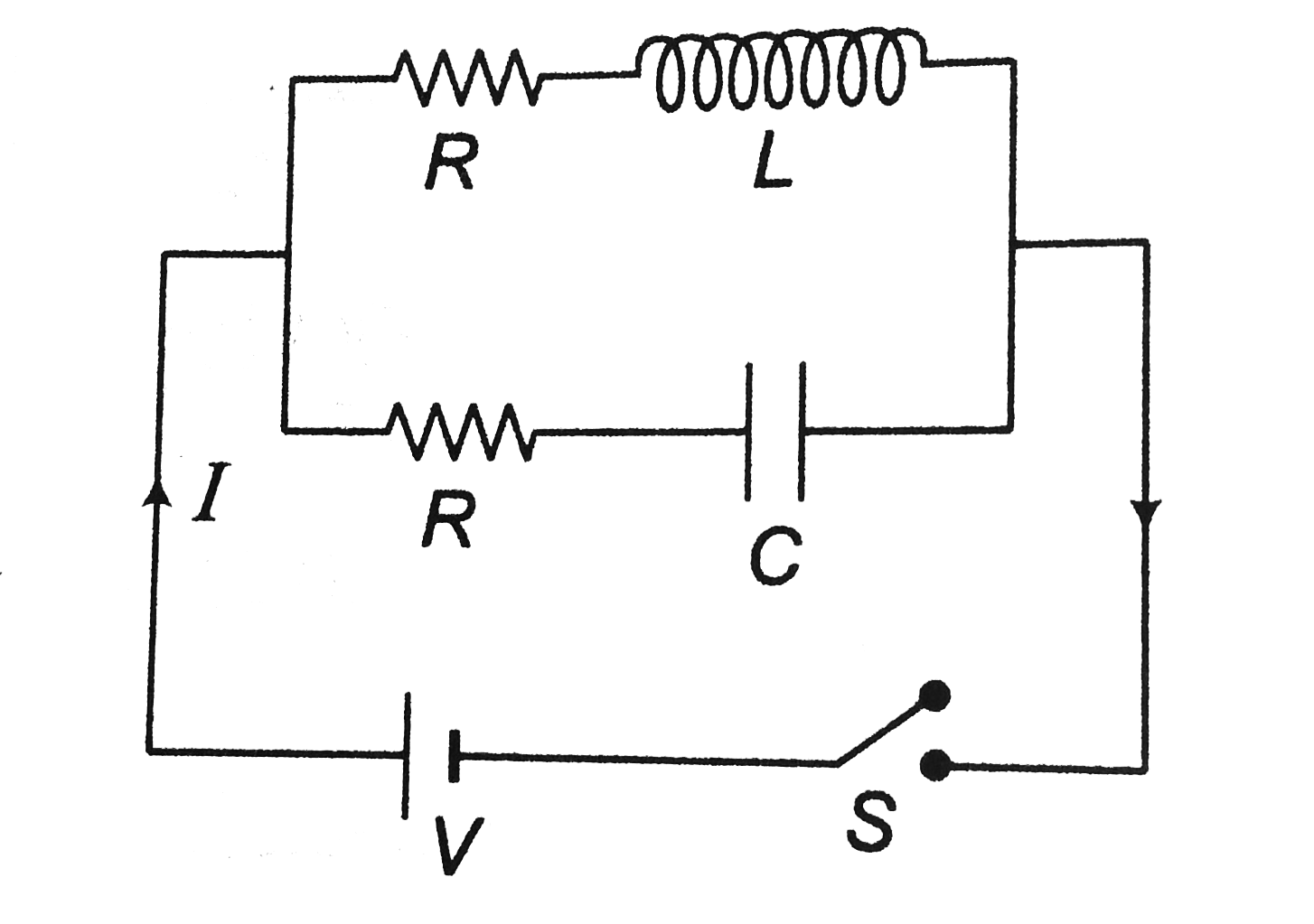
View SolutionIn the circuit diagram shown, initially there is no energy in the inductor and the capacitor, The switch is closed at t=0. Find the current I as a function of time if R=√L/C
View SolutionA potentiometer wire is 100cm long hand a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obatined at 50cm and 10cm from the positive end of the wire in the two cases. The ratio of emfs is:
View SolutionOut of the following options which one one can be used to produce a propaagating electromagnetic wave?
View SolutionA conducting frame abcd is kept in a vertical plane. A conducting rod of of mass m and length l can slide smoothly on it remaining always horizontal. The resistance of the loop is negligible and inductance is constant having value L . The rod is left from rest and allowed to fall under gravity and inductor has no initial current. A magnetic field of constant magnitude Bis present throughout the loop pointing inwards. Determine (a) position of the rod as a function of time assuming initial position of the rod to be x=0 and vertically downward as the positive x-axis. (b) the maximum current in the circuit. (c) maximum velocity of the rod
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v_0 , parallel to an infinite conducting wire carrying current i_0 . A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v_0/2 along the direction 2 of the current. At the instant t = 0 , the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop. (a) The current through the rod when it is at a distance of (a/2) from the point A of the loop. (b) Force required to maintain the velocity of the rod at that instant.
View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
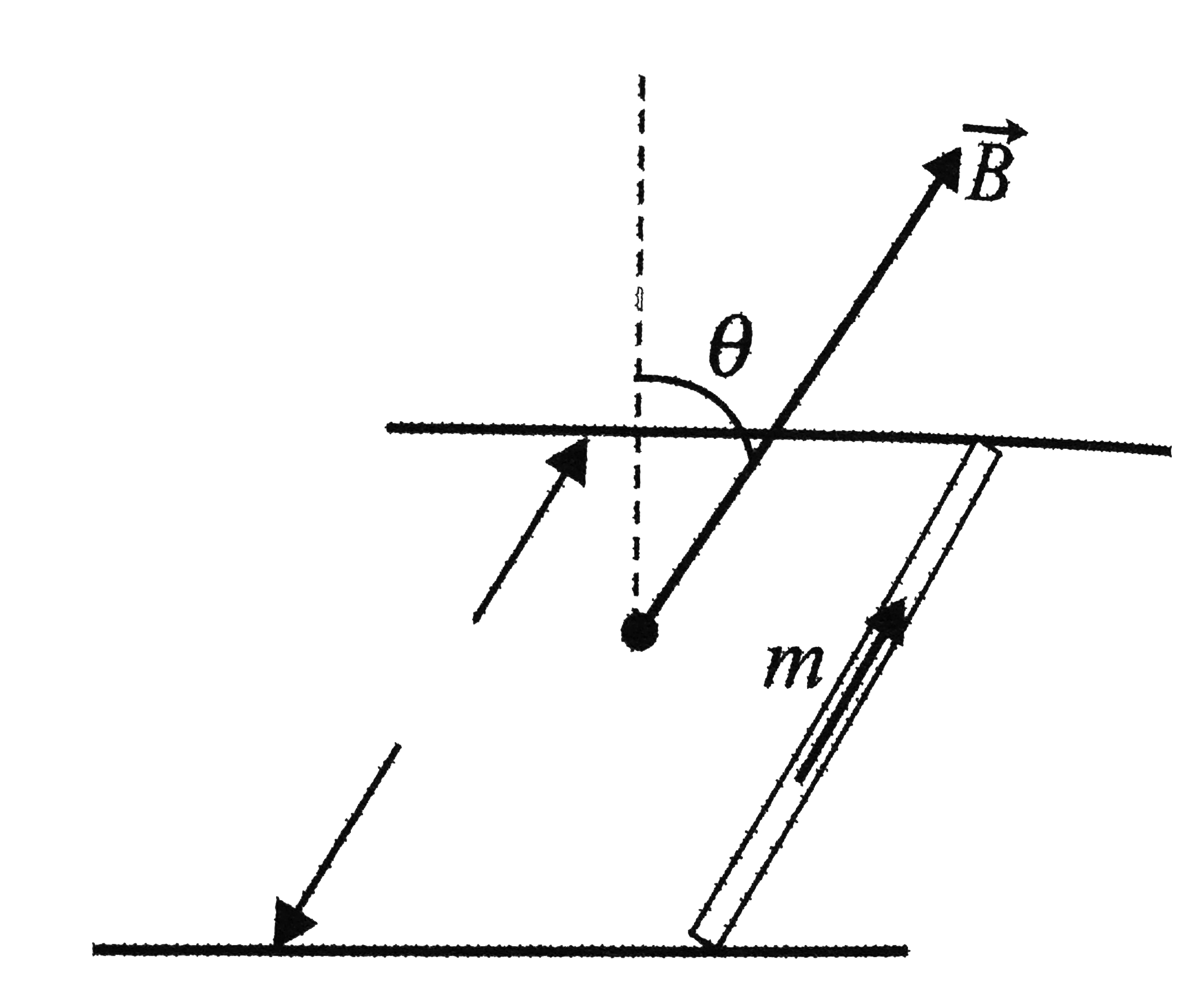
View SolutionA horizontal wire is free to slide on the verticle rails of a conducting frame as shown in figure. The wire has a mass m and length l and the resistance of the circuit is R . If a uniform magnetic field B is directed perpendicular to the frame, the terminal speed of the wire as it falls under the force of gravity is
View SolutionA loop (figure) is formed by two parallel conductores connected by a solenoid with inductance L and a conducting rod of mass m which can freely ( without friction) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B . The distance between the conductors is equal to l . At the moment t=0 the rod is imparted an initial velocity upsilon_(0) directed to the right. Find the law of its motion x(t) if the electric resistance of the loop is negligible.
View SolutionA loop is formed by two parallel conductors connected by a solenoid with inductance L=2H and a conducting rod of mass m=80g, which can freely (without fricition) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B=4T. The distance between the conductors is equal to l=4cm. At the moment t=0 the rod is imparted an initial velocity v_(0)=2 cm//s directed to the right. Find the amplitude (in cm) for the oscillations of conducting rod, if the electric resistance of the loop is negligible.
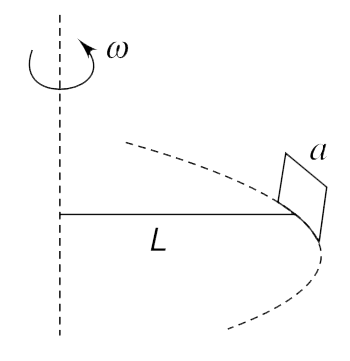
View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
View SolutionA pair of long conducting rails are held vertical at a separation l = 50 cm . The top ends are connected by a resistance of R = 0.5 Omega and a fuse (F) of negligible resistance. A conducting rod is free to slide along the rails under gravity. The whole system is in a uniform horizontal magnetic field B = 1.5 T as shown. Resistance of the rod and rails are negligible and the rod remains horizontal as it moves. The rod is released from rest. Find the minimum mass of the rod that will ensure that the fuse blows out. It is known that rating of the fuse is 4 A.
View SolutionA conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionIn the figure shown a conducting rod of length l, resistnace R and mass m is moved with a constant velocity v.The magnetic field B varies with time t as B=5t, where t is time in second.At t=0 the area of the loop containing capacitor and the rod is zero and the capacitor is uncharged.The rod started moving at t=0 on the fixed smooth conducting rails which have negligible resistance.Find (i)The current in the circuit as a function of time t.
(ii)If the above system is kept in vertical plane such that the rod can move vertically downward due of gravity and other parts are kept fixed and B=constant =B0.then find the maximum current in the circuit.
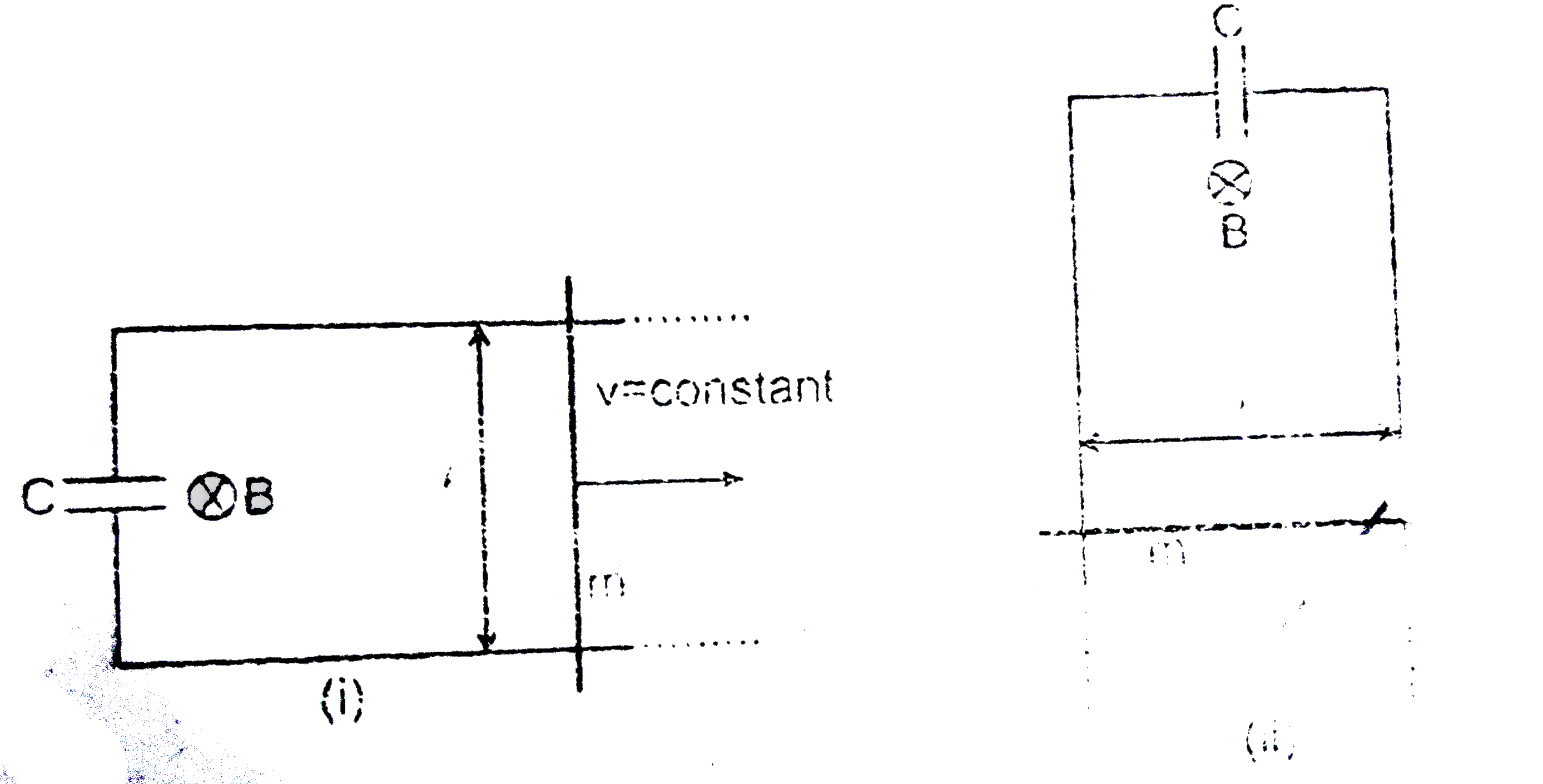
View Solution
