A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will be
−0.135Nm2C−1
−0.054Nm2C−1
0.081Nm2C−1
0.054Nm2C−1
The correct Answer is:A
To solve the problem of finding the electric flux through the surface S5 of the cube, we can follow these steps:
Step 1: Understand the Electric Field and Surface Area
The electric field is given by:
→E=−5N/C^i+3N/C^k
The cube has a side length L=0.300m. The surface S5 is one of the faces of the cube, specifically the face that is perpendicular to the x-axis.
Step 2: Determine the Area Vector
For surface S5, which is facing in the negative x-direction, the area vector →A can be expressed as:
→A=−A^i
where A is the area of the face. The area of one face of the cube is:
A=L2=(0.300m)2=0.09m2
Thus, the area vector becomes:
→A=−0.09^im2
Step 3: Calculate the Electric Flux
The electric flux Φ through the surface is given by the dot product of the electric field and the area vector:
Φ=→E⋅→A
Substituting the values:
Φ=(−5^i+3^k)⋅(−0.09^i)
Calculating the dot product:
Φ=−5⋅(−0.09)+3⋅0=0.45N m2/C
Step 4: Finalize the Result
The final electric flux through the surface S5 is:
Φ=0.45N m2/C
Summary
The electric flux passing through the surface S5 of the cube is 0.45N m2/C.
---
The electric field is given by:
→E=−5N/C^i+3N/C^k
The cube has a side length L=0.300m. The surface S5 is one of the faces of the cube, specifically the face that is perpendicular to the x-axis.
For surface S5, which is facing in the negative x-direction, the area vector →A can be expressed as:
→A=−A^i
where A is the area of the face. The area of one face of the cube is:
A=L2=(0.300m)2=0.09m2
Thus, the area vector becomes:
→A=−0.09^im2
The electric flux Φ through the surface is given by the dot product of the electric field and the area vector:
Φ=→E⋅→A
Substituting the values:
Φ=(−5^i+3^k)⋅(−0.09^i)
Calculating the dot product:
Φ=−5⋅(−0.09)+3⋅0=0.45N m2/C
The final electric flux through the surface S5 is:
Φ=0.45N m2/C
The electric flux passing through the surface S5 of the cube is 0.45N m2/C.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective type7videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total electric charge inside the cube isView SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube isView SolutionA cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
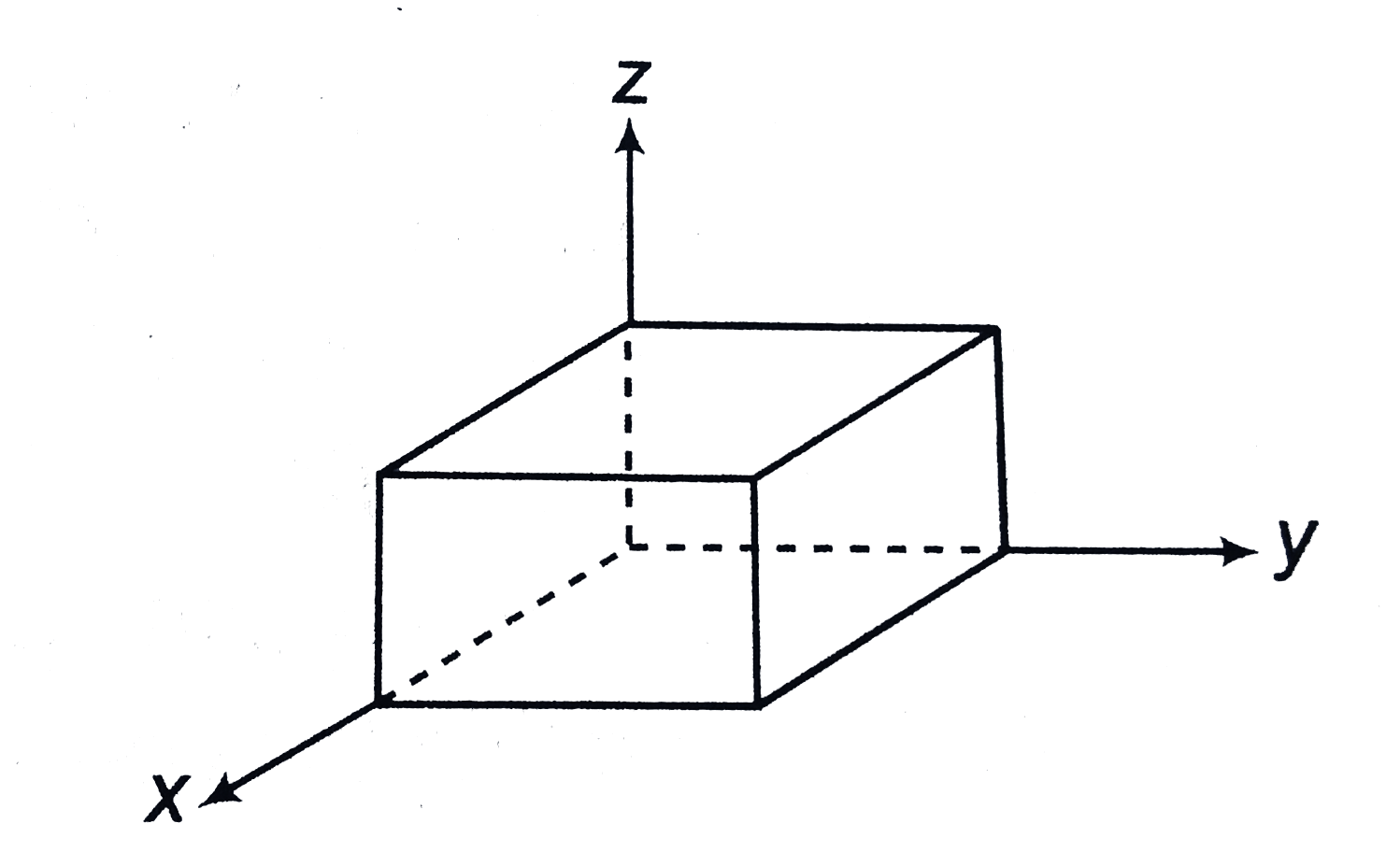 View Solution
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
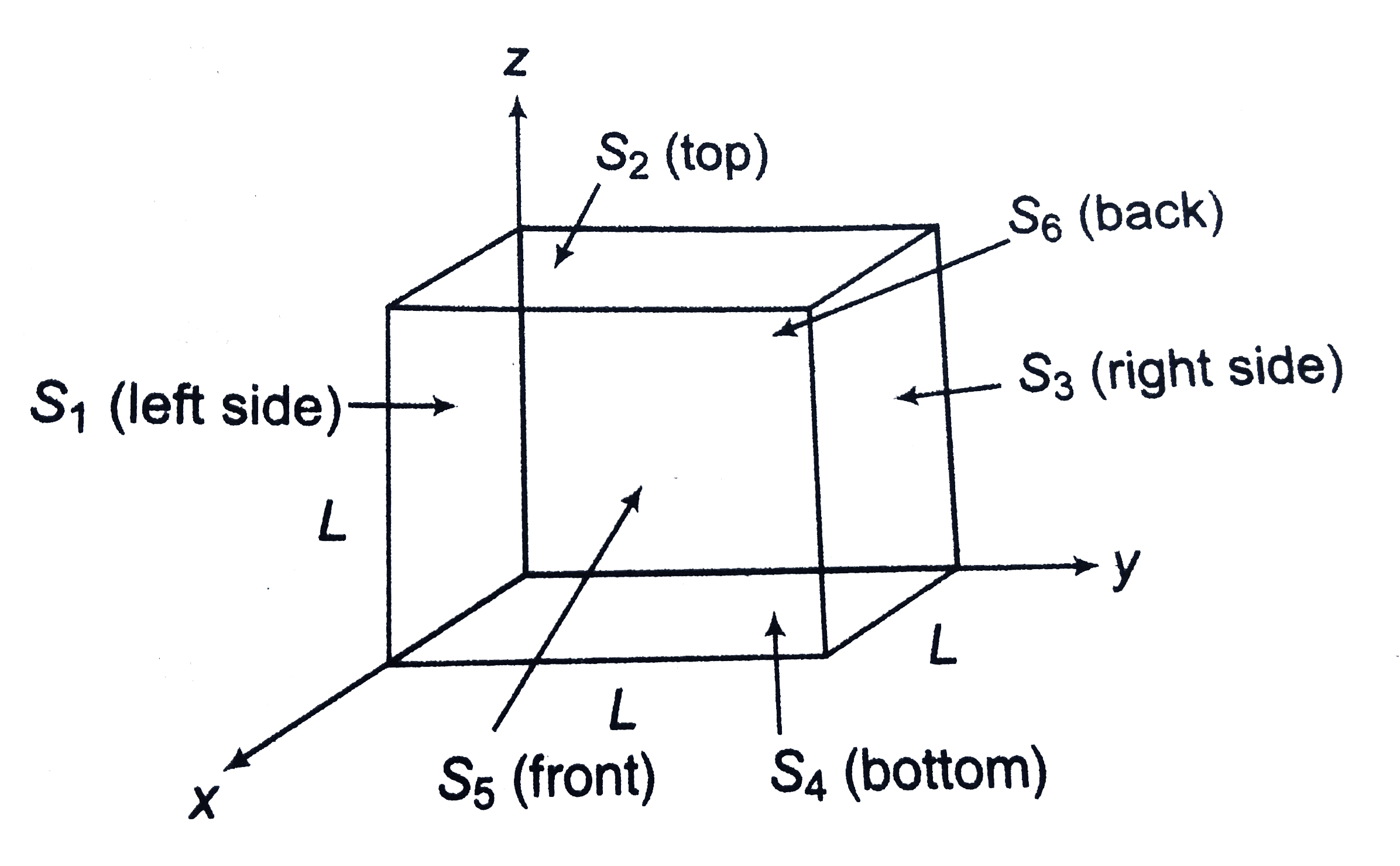
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionA bollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
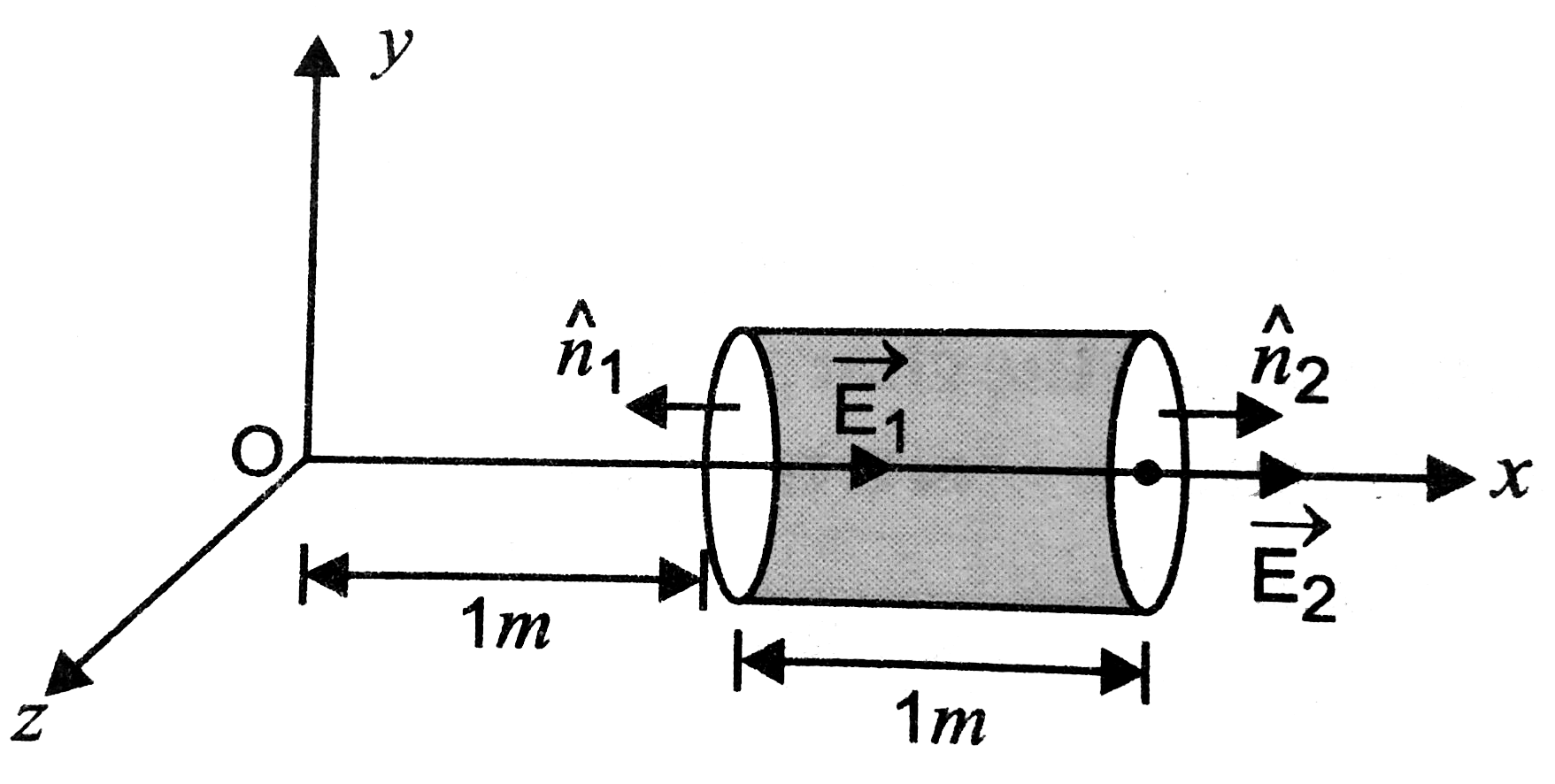 View Solution
View SolutionA hollow cylindrical box of length 0.5m and area of cross-section 20cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by →E=20xˆi, where E is NC−1 and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.View SolutionA cube of edge length l=2.50cm is positioned as shown in Fig. 3.20. A uniform magnetic field given by →B=(5.00ˆi+4.00ˆj+3.00ˆk)T exists throughout the region.
(a) Calculate the flux through the shaded face.
(b) What is the total flux through the six faces ?
 View Solution
View SolutionThe cube in figure has edge length √2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00ˆi,(b)−2.00ˆj,and(c)−3.00ˆj+4.00ˆk . (d) what is the total flux through the cube for each field ?
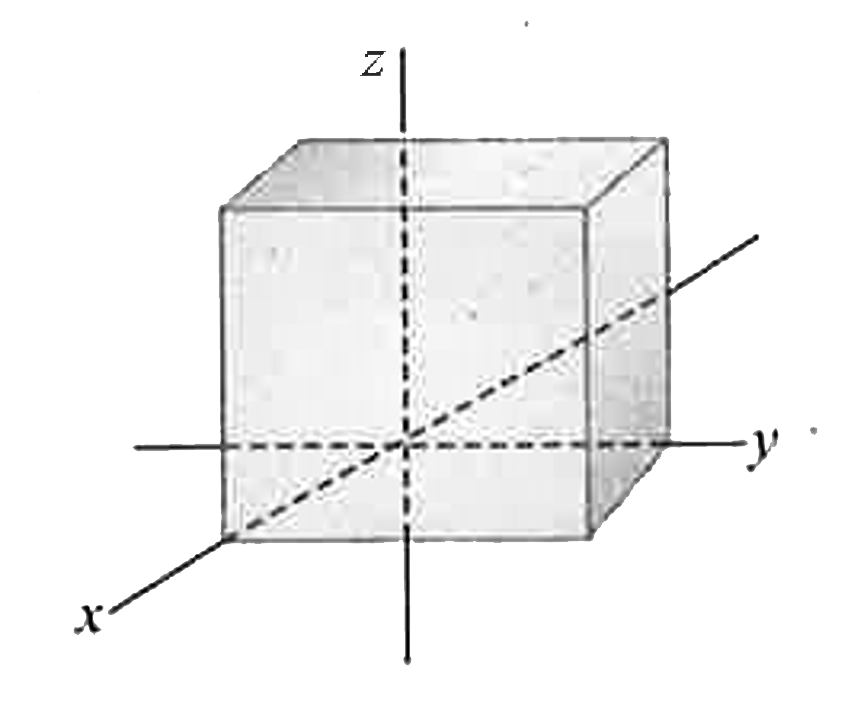 View Solution
View SolutionA surface element →ds=5ˆi is placed in an electric field →E=4ˆi+4ˆj+4ˆk. What is the electric flux emanting from the surface ?
View Solution

