A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
(a) Mg(√2+1)
(b) Mg√2
(c) Mg√2
(d) Mg(√2−1)
The correct Answer is:D
To solve the problem of finding the horizontal force required to displace a mass M kg suspended by a weightless string until the string makes an angle of 45∘ with the vertical, we can follow these steps:
Step 1: Understand the Forces Acting on the Mass
When the mass is at rest, the forces acting on it are:
- The gravitational force mg acting downward.
- The tension T in the string acting upward at an angle.
Step 2: Set Up the Equilibrium Conditions
At the angle of 45∘, the vertical and horizontal components of the forces must balance. The vertical component of the tension must equal the weight of the mass:
Tcos(45∘)=mg
Since cos(45∘)=1√2, we can rewrite this as:
T⋅1√2=mg⇒T=mg√2
Step 3: Analyze the Horizontal Forces
The horizontal component of the tension provides the necessary centripetal force to keep the mass in circular motion as it is displaced:
Tsin(45∘)=F
Again, using sin(45∘)=1√2:
F=T⋅1√2=mg√2⋅1√2=mg
Step 4: Calculate the Required Horizontal Force
From the above analysis, we see that the horizontal force F required to displace the mass such that the string makes an angle of 45∘ with the vertical is:
F=mg⋅(√2−1)
Final Answer
Thus, the horizontal force required is:
F=mg(√2−1)
When the mass is at rest, the forces acting on it are:
- The gravitational force mg acting downward.
- The tension T in the string acting upward at an angle.
At the angle of 45∘, the vertical and horizontal components of the forces must balance. The vertical component of the tension must equal the weight of the mass:
Tcos(45∘)=mg
Since cos(45∘)=1√2, we can rewrite this as:
T⋅1√2=mg⇒T=mg√2
The horizontal component of the tension provides the necessary centripetal force to keep the mass in circular motion as it is displaced:
Tsin(45∘)=F
Again, using sin(45∘)=1√2:
F=T⋅1√2=mg√2⋅1√2=mg
From the above analysis, we see that the horizontal force F required to displace the mass such that the string makes an angle of 45∘ with the vertical is:
F=mg⋅(√2−1)
Thus, the horizontal force required is:
F=mg(√2−1)
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced219videos
HEAT AND THERMODYNAMICS
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems1videos
MECHANICAL PROPERTIES OF MATTER AND FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle 45∘ with the initial vertical direction is
AMgBMg√2CMg(√2+1)D√2Mg - Question 2 - Select One
A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
AMg√2BMg(√2−1)CMg(√2+1)DMg√2 - Question 3 - Select One
A body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
A9.8N,9.8NB9.8N,19.6NC19.6N,19.6ND19.6N,9.8N
A stone of mass 1 kg is whirled in horizontal circle attached at the end of a 1 m long string. If the string makes an angle of 30∘ with vertical, calculate the centripetal force acting on the stone. (g=9.8 m/s2).
View SolutionA bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
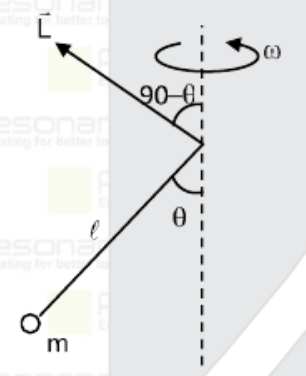 View Solution
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
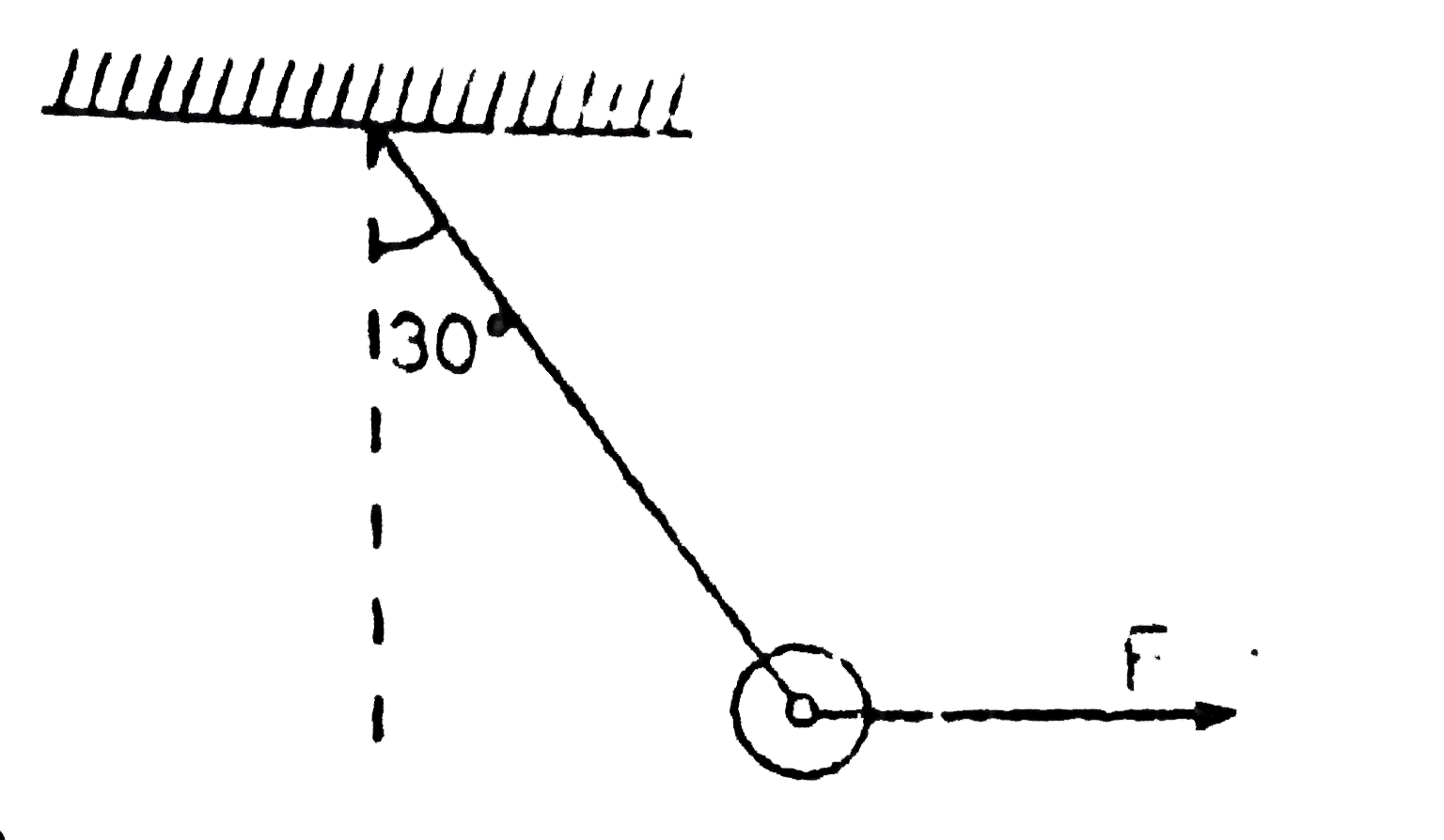 .View Solution
.View SolutionA mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
View Solution

