A non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
4qmRg
2qmRg
8qRmg
qR2mg
The correct Answer is:C
To solve the problem, we need to find the coefficient of friction (μ) between the non-conducting ring and the rough horizontal surface. The ring starts rotating after 2 seconds when a vertical time-varying magnetic field is applied.
1. Identify the given parameters:
- Charge on the ring, q
- Mass of the ring, m
- Radius of the ring, R
- Magnetic field, B(t)=4t2
- Time when the ring starts rotating, t=2s
2. Calculate the induced electric field (E):
- The magnetic flux Φ through the ring is given by:
Φ=B⋅A=B⋅πR2
- The induced electromotive force (emf) is given by Faraday's law:
emf=−dΦdt
- Since B(t)=4t2:
Φ=4t2⋅πR2
- Differentiate Φ with respect to time t:
dΦdt=ddt(4t2⋅πR2)=8t⋅πR2
- Therefore, the induced emf (which is equal to the electric field times the circumference of the ring) is:
emf=−8t⋅πR2
- The electric field E around the ring is:
E=emf2πR=−8t⋅πR22πR=−4tR
3. Calculate the electric field at t=2 seconds:
- Substitute t=2:
E=−4(2)R=−8R
- We can neglect the negative sign for magnitude:
E=8R
4. Calculate the torque due to the electric field:
- The force F acting on the ring due to the electric field is:
F=qE=q(8R)=8qR
- The torque τ1 due to this force is:
τ1=F⋅R=(8qR)⋅R=8qR2
5. Calculate the torque due to friction:
- The frictional force Ff is given by:
Ff=μmg
- The torque τ2 due to friction is:
τ2=Ff⋅R=(μmg)⋅R
6. Set the torques equal for equilibrium:
- At the point when the ring starts rotating, the torques are equal:
τ1=τ2
8qR2=μmgR
7. Solve for the coefficient of friction μ:
- Cancel R from both sides (assuming R≠0):
8qR=μmg
- Rearranging gives:
μ=8qRmg
Final Answer:
The coefficient of friction μ between the ring and the table is:
μ=8qRmg
- Charge on the ring, q
- Mass of the ring, m
- Radius of the ring, R
- Magnetic field, B(t)=4t2
- Time when the ring starts rotating, t=2s
- The magnetic flux Φ through the ring is given by:
Φ=B⋅A=B⋅πR2
- The induced electromotive force (emf) is given by Faraday's law:
emf=−dΦdt
- Since B(t)=4t2:
Φ=4t2⋅πR2
- Differentiate Φ with respect to time t:
dΦdt=ddt(4t2⋅πR2)=8t⋅πR2
- Therefore, the induced emf (which is equal to the electric field times the circumference of the ring) is:
emf=−8t⋅πR2
- The electric field E around the ring is:
E=emf2πR=−8t⋅πR22πR=−4tR
- Substitute t=2:
E=−4(2)R=−8R
- We can neglect the negative sign for magnitude:
E=8R
- The force F acting on the ring due to the electric field is:
F=qE=q(8R)=8qR
- The torque τ1 due to this force is:
τ1=F⋅R=(8qR)⋅R=8qR2
- The frictional force Ff is given by:
Ff=μmg
- The torque τ2 due to friction is:
τ2=Ff⋅R=(μmg)⋅R
- At the point when the ring starts rotating, the torques are equal:
τ1=τ2
8qR2=μmgR
- Cancel R from both sides (assuming R≠0):
8qR=μmg
- Rearranging gives:
μ=8qRmg
The coefficient of friction μ between the ring and the table is:
μ=8qRmg
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducting circular loop of radius a and resistance R is kept on a horizontal plane. A vertical time varying magnetic field B=2t is switched on at time t=0. Then
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View SolutionA non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .View Solution
.View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .View Solution
.View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
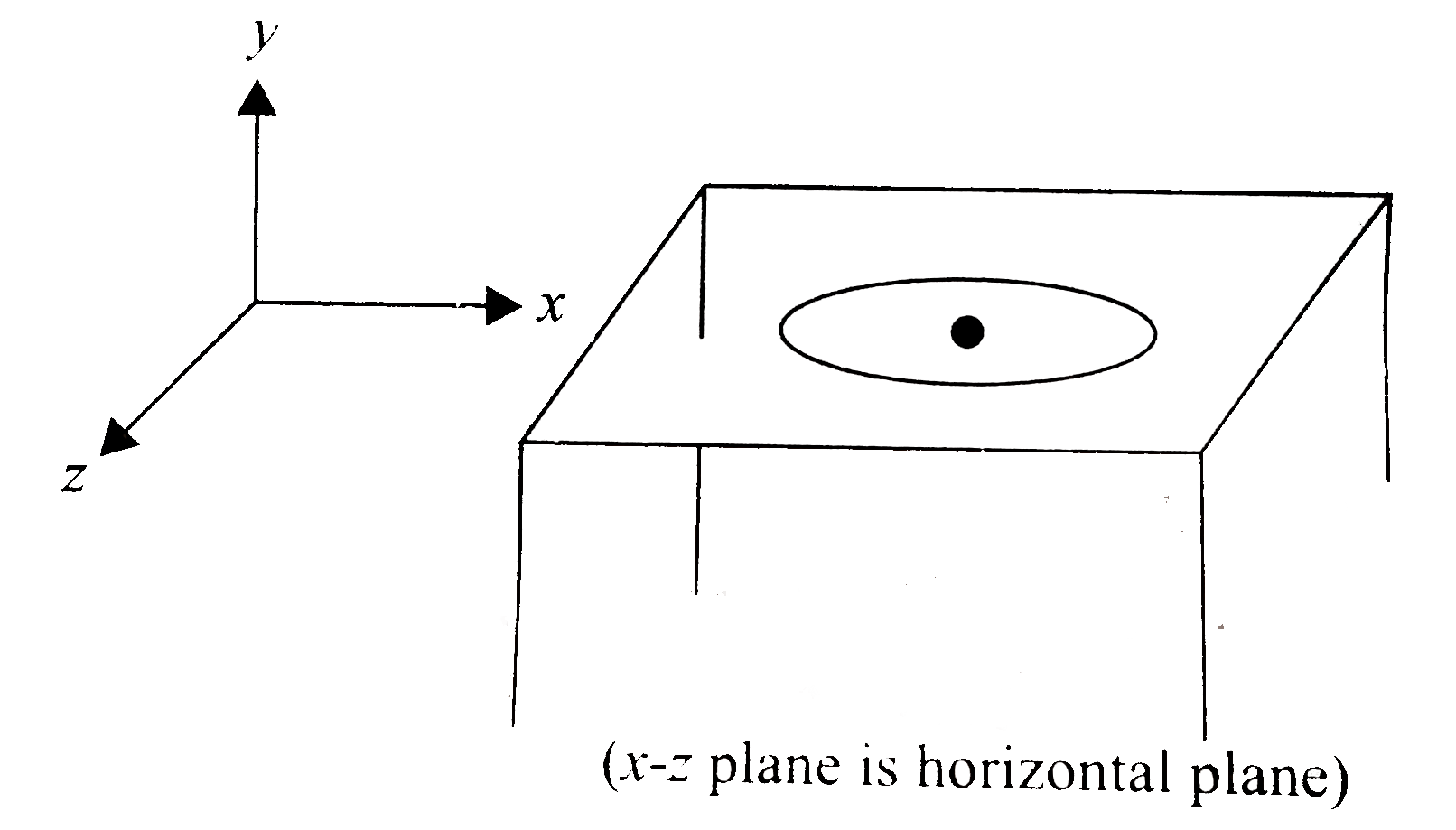
Heat generated (in kJ) through the ring till the instant when ring start toppling isView SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)
 View Solution
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
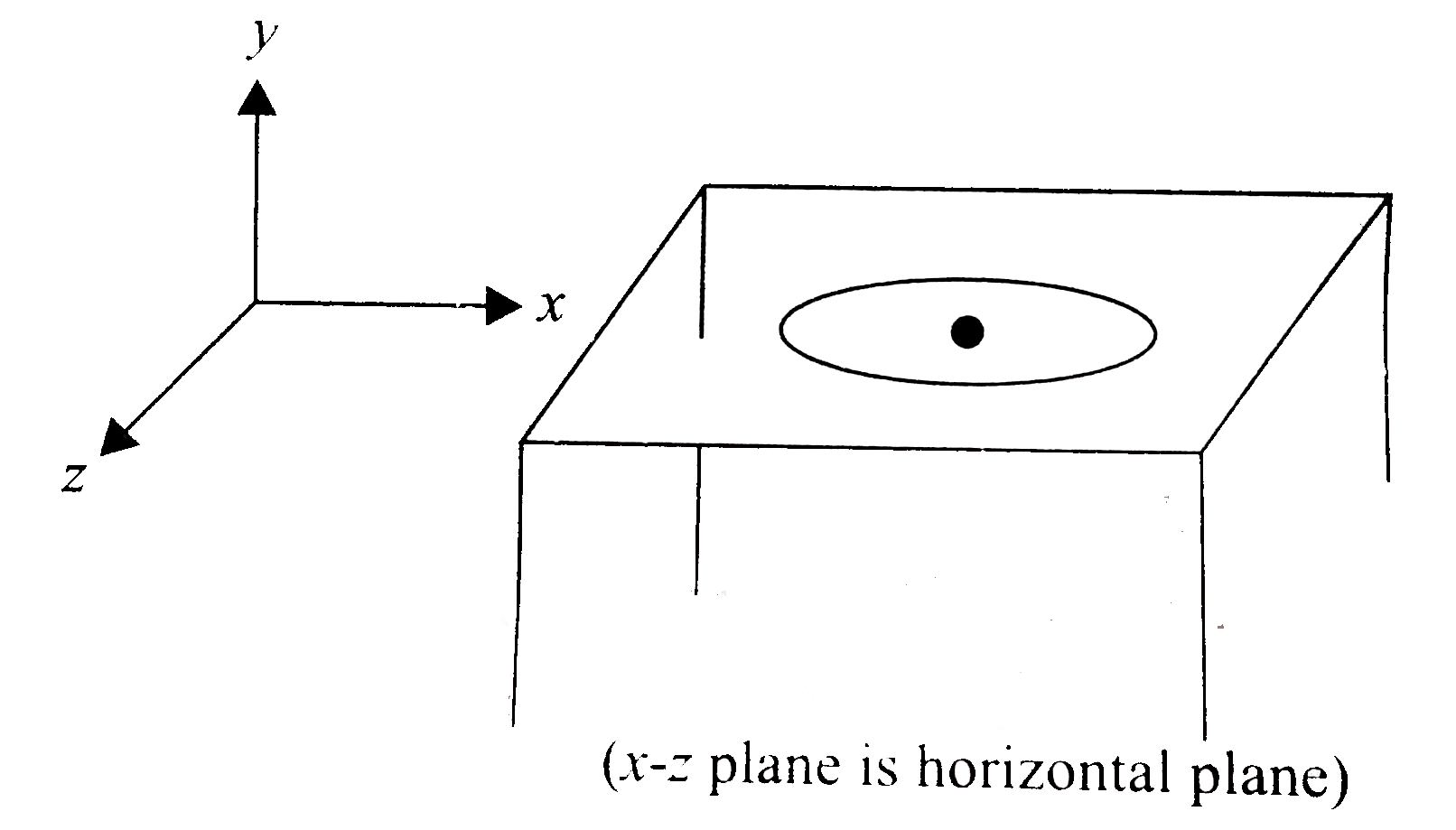
Time (in second) at which ring start toppling isView SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling isView Solution
Charge 'q' is uniformly distributed along the length of a non-coducting circular ring of mass m and radius 'a'. The ring is placed concentrically magnetic field B=kt (where k is constant) is existing perpendicular to the plane of circular region of radius 'R' as shown. The minimum coefficient of friction between the ring and the surface required to keep the ring stationary isView Solution

