A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
clockwise
anti-clockwise
zero
clockwise or anti-clockwise depending on whether the resistance is increased or decreased
The correct Answer is:c
To solve the problem, we need to analyze the situation where a small conducting circular loop is placed inside a long solenoid that carries a current. The key aspect of this problem is to understand how the changing current in the solenoid affects the magnetic flux through the loop and subsequently induces a current in the loop.
1. Understand the Setup:
- We have a long solenoid carrying a current I.
- A small conducting circular loop is placed inside this solenoid, and its plane contains the axis of the solenoid.
2. Magnetic Field Inside the Solenoid:
- The magnetic field B inside a long solenoid is given by the formula:
B=μ0nI
where μ0 is the permeability of free space, n is the number of turns per unit length of the solenoid, and I is the current through the solenoid.
3. Magnetic Flux Through the Loop:
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. Since the loop is placed such that its plane contains the axis of the solenoid, the angle between the magnetic field and the area vector is 0∘ (they are parallel), and thus:
Φ=B⋅A=μ0nI⋅A
4. Induced Current in the Loop:
- According to Faraday's law of electromagnetic induction, the induced electromotive force (emf) E in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
- If the current I in the solenoid is varied, the magnetic flux Φ through the loop will also change, leading to an induced emf.
5. Determine the Induced Current:
- The induced current Iinduced in the loop can be found using Ohm's law:
Iinduced=ER
where R is the resistance of the loop. Since the emf is induced due to the changing current in the solenoid, there will be a current induced in the loop as long as the current in the solenoid is changing.
6. Conclusion:
- Therefore, if the current in the solenoid is varied, the induced current in the loop will be non-zero. The direction of the induced current will depend on the direction of the change in current in the solenoid (Lenz's law).
Final Answer:
The current induced in the loop is non-zero when the current in the solenoid is varied.
- We have a long solenoid carrying a current I.
- A small conducting circular loop is placed inside this solenoid, and its plane contains the axis of the solenoid.
- The magnetic field B inside a long solenoid is given by the formula:
B=μ0nI
where μ0 is the permeability of free space, n is the number of turns per unit length of the solenoid, and I is the current through the solenoid.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. Since the loop is placed such that its plane contains the axis of the solenoid, the angle between the magnetic field and the area vector is 0∘ (they are parallel), and thus:
Φ=B⋅A=μ0nI⋅A
- According to Faraday's law of electromagnetic induction, the induced electromotive force (emf) E in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
- If the current I in the solenoid is varied, the magnetic flux Φ through the loop will also change, leading to an induced emf.
- The induced current Iinduced in the loop can be found using Ohm's law:
Iinduced=ER
where R is the resistance of the loop. Since the emf is induced due to the changing current in the solenoid, there will be a current induced in the loop as long as the current in the solenoid is changing.
- Therefore, if the current in the solenoid is varied, the induced current in the loop will be non-zero. The direction of the induced current will depend on the direction of the change in current in the solenoid (Lenz's law).
The current induced in the loop is non-zero when the current in the solenoid is varied.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionShow a conduction loop placed near a long, straight wire carrying current i as shown. If the current increases continuously, find the direction of the induced current in the loop.
 View Solution
View SolutionA circular loop is placed near a current carrying conductor as shown in figure. Find the direction of induced current, if the current, in the wire is decreasing.
 View Solution
View SolutionWhen the current through a solenoid increases at a constant rate, the induced current in the solenoid
View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.
 View Solution
View SolutionMagnetic lines of force inside a current carrying solenoid are
View SolutionA square conducting loop is placed in the neighbourhood of a coplaner long straight wire carrying a current i.
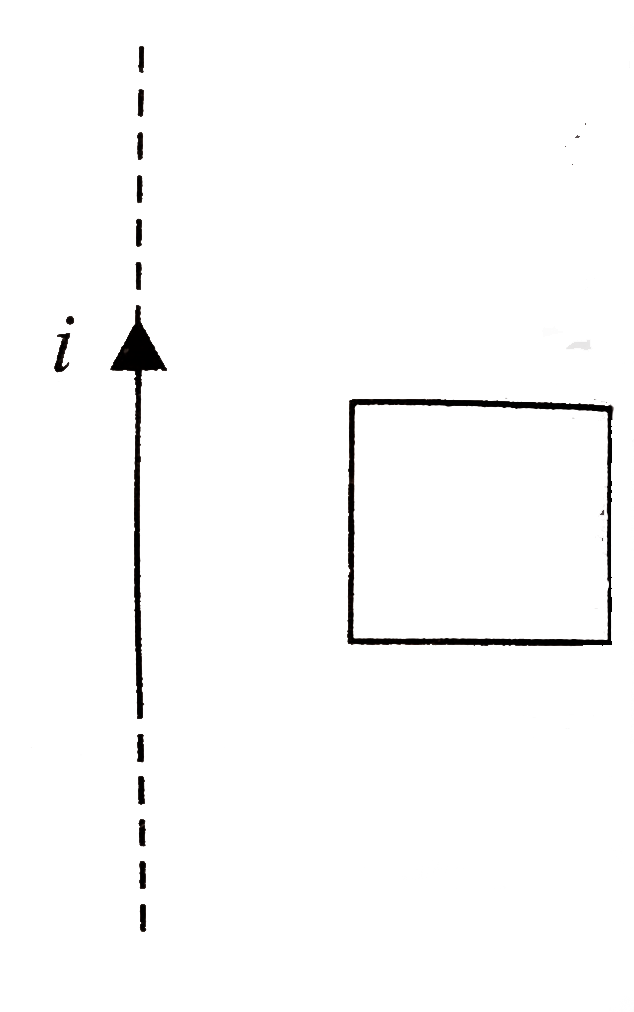 View Solution
View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
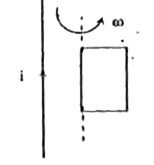 View Solution
View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the axis of the loop is in
View SolutionIn Fig. there is a conducting loop ABCDEF of resistance λ per unit length placed near a long straight current-carrying wire. The dimension are shows in the figure. The long wire lies in the plane of the loop. The current in the long wire varies as I=I0(t).

The emf induced in the closed loop isView Solution

