Question

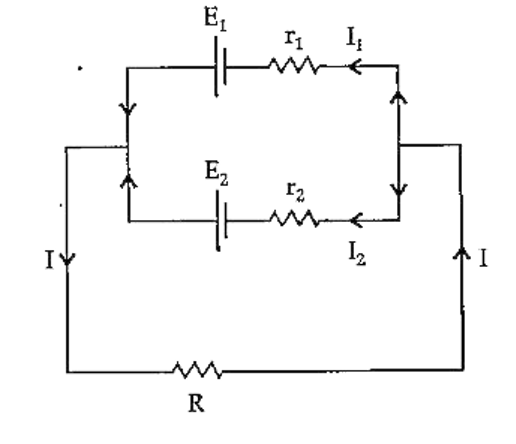
A student connects a cell of emf ${\epsilon }_2$ and internal resistance $r_2$, with a cell of emf ${\epsilon }_1$ such that their combinationhas a net internal resistance less then $r_1$. This combination in the connected across a resistance $R$. Draw a circuit of the 'set up' and obtain an expression for the current flowing through the resistance $R$

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the Configuration
We have two cells connected in parallel, one with emf \( \epsilon_1 \) and internal resistance \( r_1 \), and the other with emf \( \epsilon_2 \) and internal resistance \( r_2 \). The goal is to find the current flowing through an external resistance \( R \) when these cells are connected.

Step 2: Draw the Circuit Diagram
The circuit diagram will look like this:

```
+---( r1 )---+
| |
( ε1 ) ( ε2 )
| |
+---( r2 )---+
|
R
|
GND
```

Step 3: Calculate the Equivalent EMF
When two cells are connected in parallel, the equivalent emf \( \epsilon \) is given by the formula:

\( \epsilon = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2} \)

This formula accounts for the contributions of both cells and their internal resistances.

Step 4: Calculate the Equivalent Resistance
The equivalent internal resistance \( r \) for the two cells in parallel is given by:

\( r = \frac{r_1 r_2}{r_1 + r_2} \)

Step 5: Apply Ohm's Law to Find Current
The total current \( I \) flowing through the external resistance \( R \) can be calculated using Ohm's Law:

\( I = \frac{\epsilon}{R + r} \)

Substituting the expressions for \( \epsilon \) and \( r \):

\( I = \frac{\frac{\epsilon_1 r_2 + \epsilon_2 r_1}{r_1 + r_2}}{R + \frac{r_1 r_2}{r_1 + r_2}} \)

Step 6: Simplify the Expression
To simplify the expression for \( I \):

1. The denominator can be simplified as follows:
\( R + \frac{r_1 r_2}{r_1 + r_2} = \frac{(R + r_1 + r_2) (r_1 + r_2)}{r_1 + r_2} \)

2. Thus, the current expression becomes:
\( I = \frac{(\epsilon_1 r_2 + \epsilon_2 r_1)}{(R + r_1 + r_2)} \)

Final Expression for Current
The final expression for the current flowing through the resistance \( R \) is:

\( I = \frac{\epsilon_1 r_2 + \epsilon_2 r_1}{R(r_1 + r_2) + r_1 r_2} \)